跳至主要內容

Exploratory Data Analysis

Hirsuntech大约 35 分钟

Exploratory Data Analysis

关于EDA详细说明，请查看 https://www.itl.nist.gov/div898/handbook/eda/eda.htmopen in new window

探索性数据分析（EDA）是一种数据分析的方法/哲学，它采用各种技术（主要是图形技术）来

  1. 最大限度地了解一个数据集的情况。
  2. 揭示潜在的结构。
  3. 提取重要的变量。
  4. 检测异常值和反常现象。
  5. 测试基本假设。
  6. 开发简明的模型；
  7. 确定最佳因素设置。

EDA 方法

EDA方法正是这种方法，它不是一套技术，而是一种关于如何进行数据分析的态度/哲学。

EDA与统计图形不尽相同，尽管这两个术语几乎可以互换使用。统计图形是一系列技术的集合--都是基于图形的，并且都集中在一个数据特征方面。EDA包含了一个更大的场所；EDA是一种数据分析的方法，它推迟了关于数据遵循何种模型的通常假设，而采用更直接的方法，让数据本身来揭示其潜在的结构和模型。EDA不是一个单纯的技术集合；EDA是一种关于我们如何剖析数据集的哲学；我们寻找什么；我们如何寻找；以及我们如何解释。诚然，EDA大量使用我们称之为 "统计图形 "的技术集合，但它与统计图形本身并不完全相同。

大多数EDA技术都是图形性质的，只有少数定量技术。之所以严重依赖图形，是因为就其本质而言，EDA的主要作用是开放性的探索，而图形给了分析者无与伦比的力量，诱使数据揭示其结构的秘密，并随时准备获得一些新的，往往是未曾预料到的，对数据的洞察力。结合我们所拥有的自然模式识别能力，图形当然提供了无与伦比的力量来实现这一目标。

EDA中采用的特殊图形技术通常很简单，由以下各种技术组成。

  1. 绘制原始数据（如数据痕迹、直方图、双直方图、概率图、滞后图、块图和尤登图。
  2. 绘制简单的统计数据，如平均数图、标准差图、箱形图和原始数据的主效应图。
  3. 对这些图进行定位，以便最大限度地提高我们的自然模式识别能力，如每页使用多个图。
一个研究案例

1. 确定的研究的课题

作为第一个例子，我们将从一个简单的问题开始：美国婴儿的平均出生体重是多少？为了回答这样的问题，我们必须找到一个合适的数据集，或者运行一个实验来收集它。然后，我们必须将数据输入我们的开发环境，并为分析做准备，这涉及到清洗和验证。

美国婴儿的出生数据的研究

  • 平均值，最大值，最小值，平均值
  • 各列数据之间的相关性

对于这个问题，我们将使用来自全国家庭增长调查的数据，该数据可从国家卫生统计中心获得。2013-2015 数据集包含有关美国女性及其子女的代表性样本的信息。

2. 预览数据

当你使用像NSFG这样的数据集时，仔细阅读文件是很重要的。如果你对一个变量的解释不正确，你可能会产生胡言乱语的结果而不自知。因此，在你开始编码之前，你需要熟悉NSFG的编码手册，其中描述了每个变量。

下面是NSFG编码手册中关于 "BIRTHWGT_OZ1 "的文件。

1654621783227.png

区分下列描述词

  • df.shape: 描述行列数量
  • df.infoopen in new window: 大略浏览数据表
  • df.head(): 查看头部前几行
  • df.describe(): 查看数据平均值，最大最小值。
  • df.value_counts(): 统计每一种值有几个

3. 数据清理

在我们用这些数据做任何事情之前，我们必须对其进行验证。验证的一个部分是确认我们对数据的解释是否正确。我们可以使用value_counts()来查看哪些值出现在磅中，以及每个值出现的次数。默认情况下，结果是以最频繁的值为先进行排序的，所以我使用sort_index()按值排序，将最轻的婴儿放在前面，最重的婴儿放在最后。正如我们所期望的，最频繁的数值是6-8磅，但也有一些非常轻的婴儿，一些非常重的婴儿，还有两个数值，98和99，表明数据缺失。

我们可以通过将结果与编码簿进行比较来验证，编码簿中列出了各种数值及其频率。这里的结果与编码表一致，所以我们有一些信心，我们正在正确地阅读和解释数据。

另一种验证数据的方法是使用describe()，它可以计算出平均数、标准差、最小值和最大值等汇总统计数据。下面是磅数的结果。 count是数值的数量。最小值和最大值是0和99，第50个百分位数，也就是中位数，是7。平均数大约是8.05，但这并不意味着什么，因为它包括了特殊值98和99。

replace()方法做了我们想要的事情；它接收了一个我们想要替换的数值列表和我们想要替换的数值。 np dot nan表示我们从NumPy库中获取特殊的数值NaN，它被导入为np。replace()的结果是一个新的系列，我将其赋值回磅数。请记住，原始系列的平均值约为8点05磅。新系列的平均数是6点7磅。当你去掉几个99磅的婴儿时，这就有很大的不同了。

4. 数据整理

现在我们想把磅和盎司合并成一个系列，包含出生时的总重量。算术运算符与系列对象一起工作；因此，为了从盎司转换到磅，我们可以除以16（一磅有16盎司）。然后，我们可以将两个系列对象相加，得到总数。下面是结果。平均数约为7点1，这比我们在加入盎司部分之前得到的要多一点。现在我们已经接近于回答我们最初的问题，即美国婴儿的平均出生体重，但正如我们在下一课中所看到的，我们还没有达到目的。

在回答我们的问题之前，我们还需要做一件事：重新采样。NSFG 并不完全代表美国人口；根据设计，某些组比其他组更可能出现在样本中；他们被“过度采样”。过采样有助于确保您在每个子组中都有足够的人来获得可靠的统计数据，但它会使分析变得更加复杂。但是，我们可以通过重采样来纠正过采样。

5. 数据可视化和数据探索

我们使用来自 NSFG 的数据来计算以磅为单位的出生体重，并将结果存储在名为birth_weight 的系列中。让我们看看这些值的分布是什么样的。

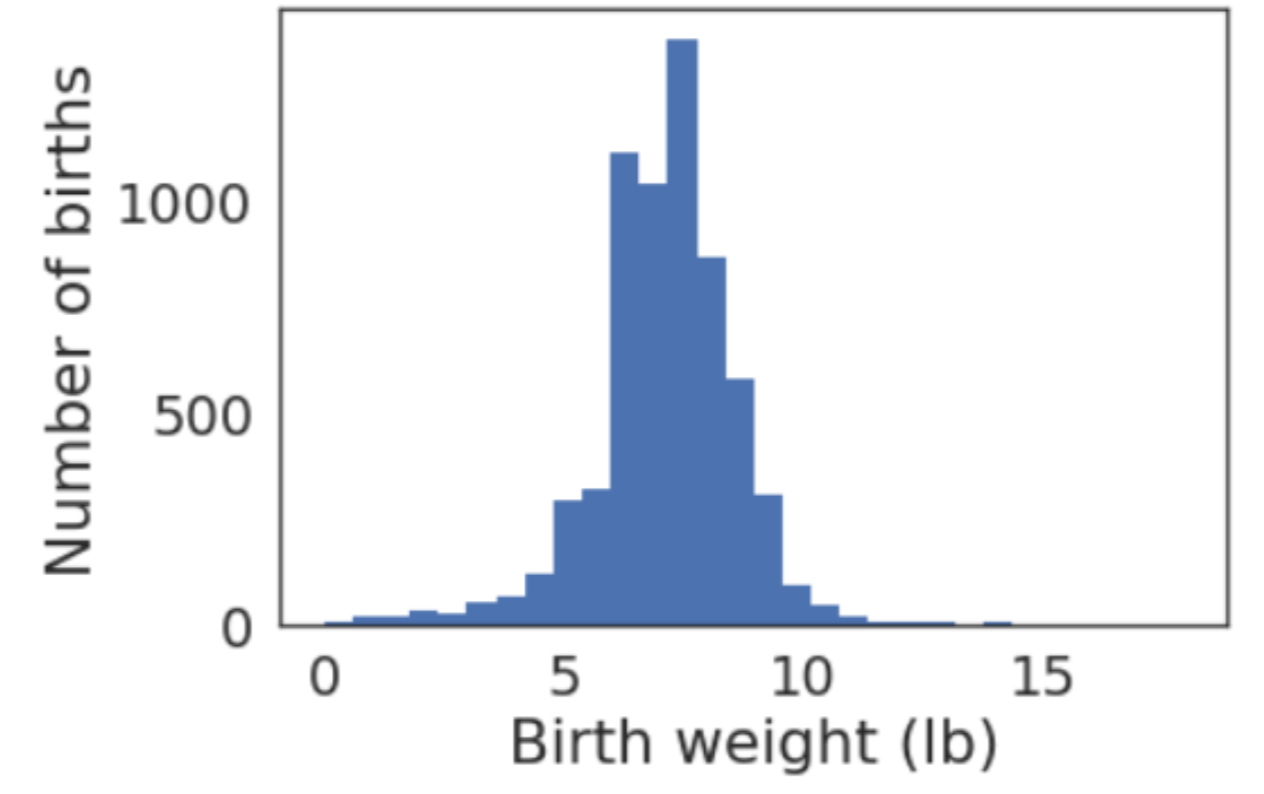
1654621609937.png

这里是结果的样子。X轴是以磅为单位的出生体重，分为30个档次。y轴是每个仓内的出生数量。这个分布看起来有点像钟形曲线，但是尾巴在左边比右边长；也就是说，轻婴儿比重婴儿多。这是有道理的，因为这个分布包括一些早产的婴儿。最常见的怀孕时间是39周，也就是 "足月"；"早产 "通常被定义为小于37周。

要想知道哪些婴儿是早产儿，我们可以使用prglngth列，它记录了以周为单位的怀孕长度。当你将一个系列与一个值进行比较时，其结果是一个布尔系列；也就是说，每个元素都是一个布尔值，是真还是假。在本例中，每个早产儿都是True，否则就是False。我们可以使用head()来查看前5个元素。

如果你计算布尔系列的总和，它把 "真 "当作 "1"，把 "假 "当作 "0"，所以总和就是 "真 "的数量，也就是早产儿的数量，大约是3700。如果你计算平均值，你会得到Trues的分数；在这种情况下，它接近0.4；也就是说，在这个数据集中大约有40%的新生儿是早产儿。。

我们可以使用布尔系列作为过滤器；也就是说，我们可以只选择满足某个条件或符合某些标准的行。例如，我们可以使用早产儿和括号运算符从出生体重中选择数值，因此早产儿_体重包含早产儿的出生体重。要选择足月的婴儿，我们可以使用tilde操作符，这是 "逻辑NOT "或反转；它使Trues为假，Falses为真。毫不奇怪，足月婴儿平均比早产婴儿重。

NSFG数据集包括一个变量 "agecon"，记录了每次怀孕的年龄。

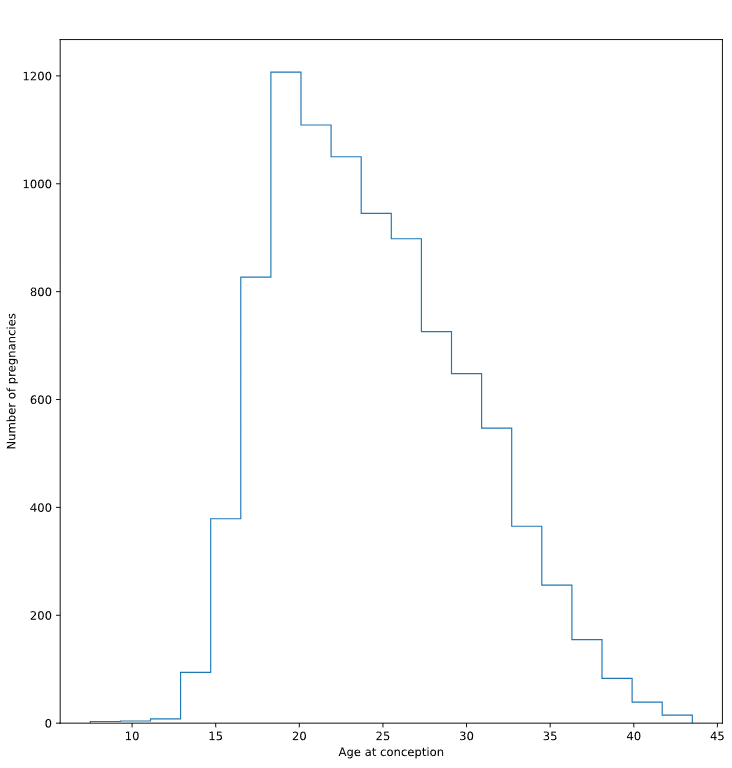
1654621903907.png

前面的练习中，计算了足月婴儿的平均出生体重；我们过滤掉了早产婴儿，因为他们的体重分布是不同的。
多胞胎的体重分布也不同，如双胞胎和三胞胎，也要把它们过滤掉，看看对平均值有什么影响。

EDA小结

  • Import, clean, and validate
  • Visualize distributions
  • Explore relationships between variables
  • Explore multivariate relationships

导入和清理数据，以及检查错误和其他特殊情况: 如果跳过这些步骤，它可能会再次困扰您。花时间清理和验证数据可以使您免于尴尬，有时甚至是代价高昂的错误。

PMF & CDF & PDF

PMF

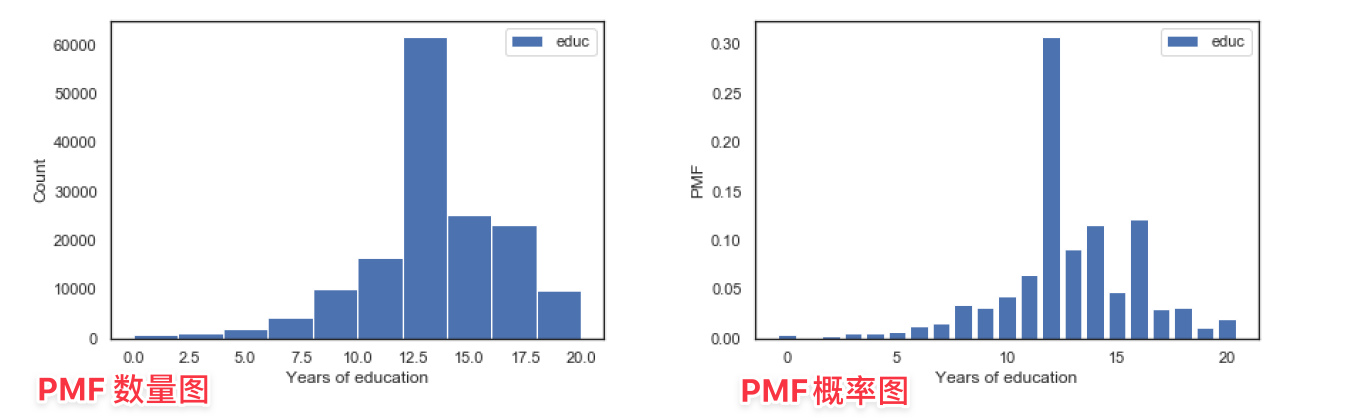
1654668252351.png
1654668252351.png

使用 plt.hist 可以绘制 PMF

CDF

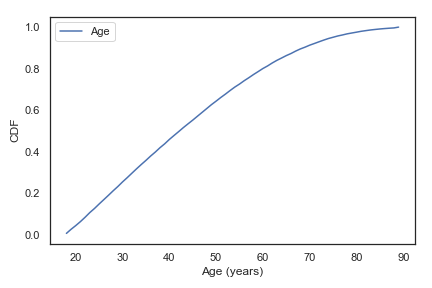
1654668279487.png1654668304010.png

当数据具有大量唯一值时，PMF不能很好地工作，CDF有时能更好的表现数据

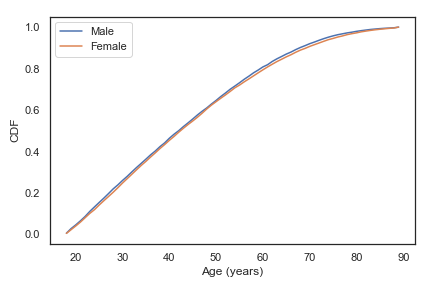
1654668379892.png
1654668379892.png
pdf = count / sum(count)
cdf = np.cumsum(pdf)
plt.plot(bins_count[1:], cdf, label="CDF")
plt.show()

PDF

使用 sns.distplot() 或者 df.plot.kde()来绘制KDE

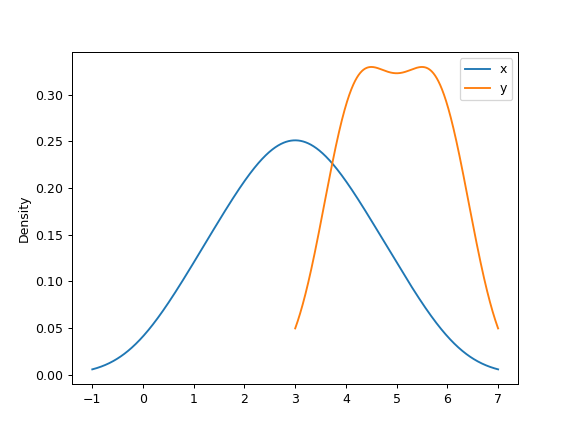
1654669710598.png

总结

总结一下三种可视化分布的方法，PMF、CDF和PDF。一般来说，

  • 在探索数据的时候会使用 CDF。
    • 我认为它们能提供最好的视图，而不会被噪音所干扰。
    • CDFs的最大缺点是它们不太为人所知。
  • 如果我向不熟悉 CDF 的听众展示结果，我会对有少量独特数值的分布使用 PMF。
  • 如果有大量的数值，则使用 PDF。

分布建模

正态分布PDF建模

正态分布，也被称为高斯分布。

1654683920071.png

举例，下面将正态分布和数据的分布画到一个图上以进行对比。

import numpy as np
from scipy.stats import norm

# Extract realinc and compute its log
income = gss['realinc']
log_income = np.log10(income)
mean = log_income.mean()
std = log_income.std()

# 建立标准轴
# 从 -3 到 3 平均取样，默认个数为 num = 50, 作为x轴标点
xs = np.linspace(2, 8)
# 参考xs轴，以正态分布取样
ys = norm(mean, std).pdf(xs)
plt.plot(xs, ys, color='gray')
plt.show()

>>> xs
array([2.        , 2.12244898, 2.24489796, 2.36734694, 2.48979592,
       2.6122449 , 2.73469388, 2.85714286, 2.97959184, 3.10204082,
       3.2244898 , 3.34693878, 3.46938776, 3.59183673, 3.71428571,
       3.83673469, 3.95918367, 4.08163265, 4.20408163, 4.32653061,
       4.44897959, 4.57142857, 4.69387755, 4.81632653, 4.93877551,
       5.06122449, 5.18367347, 5.30612245, 5.42857143, 5.55102041,
       5.67346939, 5.79591837, 5.91836735, 6.04081633, 6.16326531,
       6.28571429, 6.40816327, 6.53061224, 6.65306122, 6.7755102 ,
       6.89795918, 7.02040816, 7.14285714, 7.26530612, 7.3877551 ,
       7.51020408, 7.63265306, 7.75510204, 7.87755102, 8.        ])
>>> ys
array([2.16260226e-07, 1.00555769e-06, 4.30979761e-06, 1.70265363e-05,
       6.20033692e-05, 2.08124792e-04, 6.43949619e-04, 1.83653628e-03,
       4.82799354e-03, 1.16991254e-02, 2.61312183e-02, 5.38003955e-02,
       1.02101195e-01, 1.78605870e-01, 2.87991838e-01, 4.28039825e-01,
       5.86418582e-01, 7.40543912e-01, 8.62012285e-01, 9.24901837e-01,
       9.14739379e-01, 8.33908991e-01, 7.00744156e-01, 5.42775029e-01,
       3.87525051e-01, 2.55034686e-01, 1.54709958e-01, 8.65081114e-02,
       4.45876868e-02, 2.11832504e-02, 9.27662080e-03, 3.74460969e-03,
       1.39329428e-03, 4.77857825e-04, 1.51068562e-04, 4.40219256e-05,
       1.18245201e-05, 2.92763923e-06, 6.68145641e-07, 1.40554343e-07,
       2.72544200e-08, 4.87134813e-09, 8.02566333e-10, 1.21879946e-10,
       1.70609464e-11, 2.20137247e-12, 2.61820405e-13, 2.87033770e-14,
       2.90056130e-15, 2.70178414e-16])
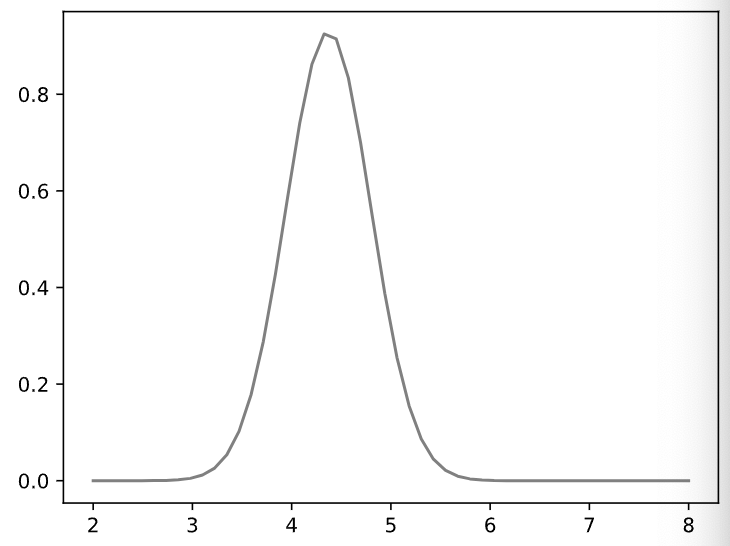
1654676762938.png
# 建立数据轴
# 参数 bw_method 用于重新取样防止过拟合
log_income.plot.kde(bw_method=0.5)
plt.show()
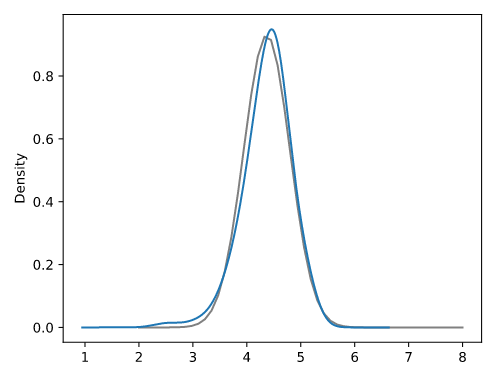
1654677081562.png

因此可以说 log_income 呈现正态分布。

正态分布CDF建模

# Evaluate the model CDF
xs = np.linspace(2, 5.5)
ys = norm(mean, std).cdf(xs)

# Plot the model CDF
plt.clf()
plt.plot(xs, ys, color='gray')

# Create and plot the Cdf of log_income
# Cdf 是一个自定义函数
Cdf(log_income).plot()
    
# Label the axes
plt.xlabel('log10 of realinc')
plt.ylabel('CDF')
plt.show()
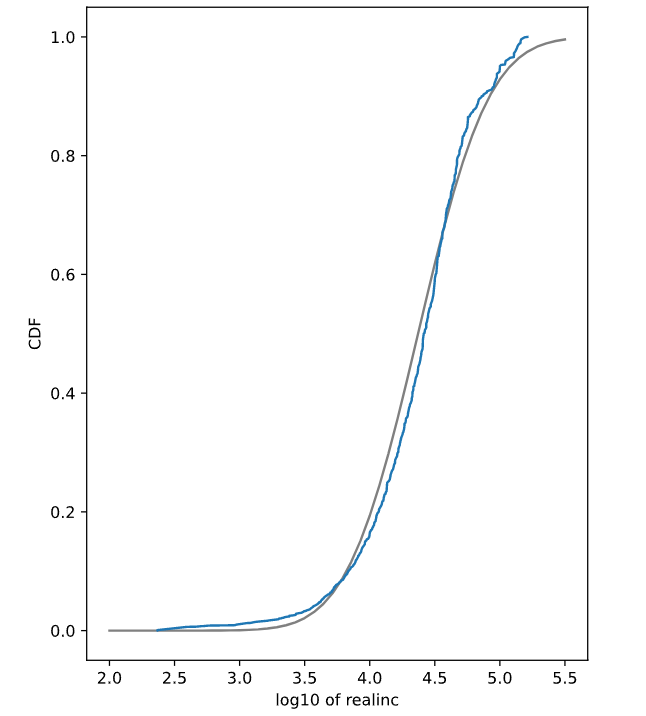
1654677402396.png

Figure Fix

过渡采样点处理

brfss = pd.read_hdf('brfss.hdf5', 'brfss')
height = brfss['HTM4']
weight = brfss['WTKG3']
plt.plot(height, weight, 'o')
plt.xlabel('Height in cm')
plt.ylabel('Weight in kg')
plt.show()
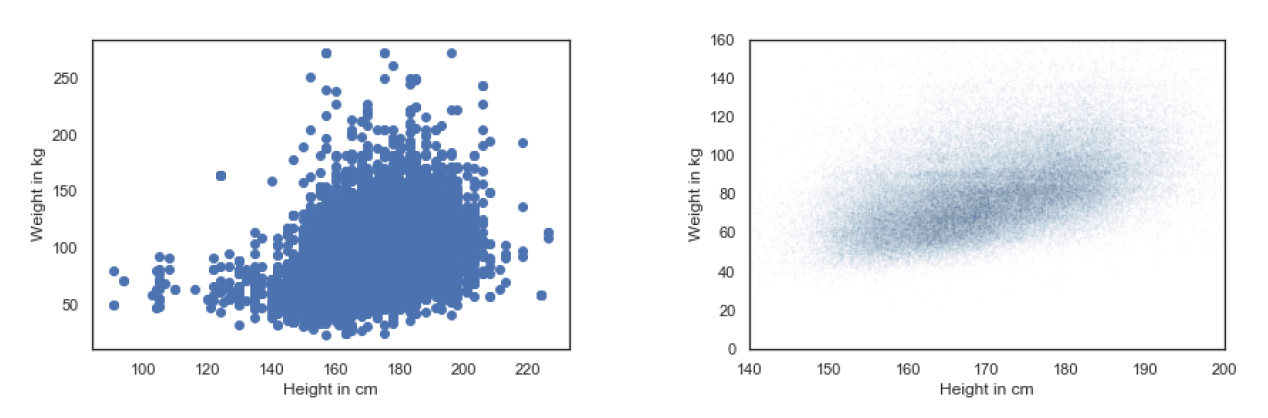
1654682883948.png

左图由于过度采样，导致点扎堆，无法获取更直观的信息。我们的目标是加工其成为右面的图像。

# 调整点的样式，使用 "o", 而不是使用·
# markersize 调整点的大小
# alpha调整点的透明度，以识别重叠
plt.plot(x = height, y = weight, 'o', markersize=1, alpha=0.02)
plt.show()
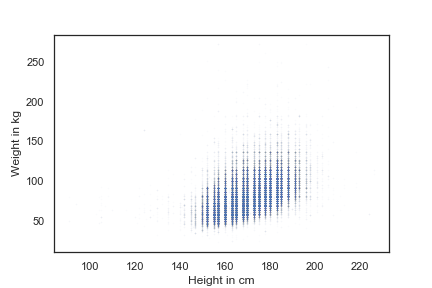
1654683070394.png
1654683070394.png

由于点过度集中，不妨添加一些抖动(Jittering)

# size 指定 series 的长度,即随机数的个数
height_jitter = height + np.random.normal(0, 2, size=len(brfss))
weight_jitter = weight + np.random.normal(0, 2, size=len(brfss))
plt.plot(height_jitter, weight_jitter, 'o', markersize=1, alpha=0.01)
plt.show()
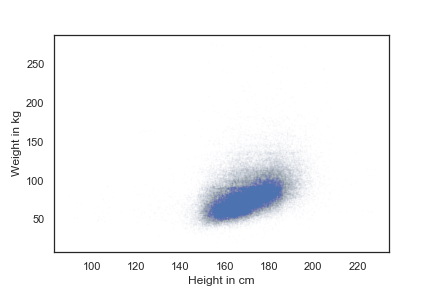
1654683979824.png
1654683979824.png

由于点集中在一小块，不妨设置一下轴的聚焦

plt.plot(height_jitter, weight_jitter, 'o', markersize=1, alpha=0.02)
plt.axis([140, 200, 0, 160])
plt.show()
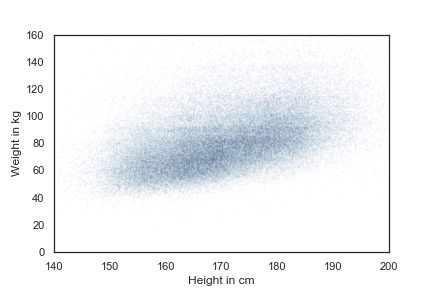
1654684054013.png
1654684054013.png

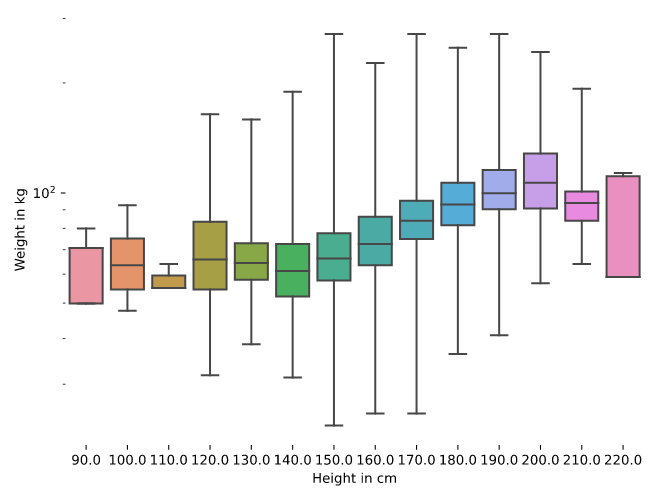
改变轴的scale

# Make a box plot
sns.boxplot(x = "_HTMG10", y = "WTKG3", data = data, whis=10)

# Plot the y-axis on a log scale
plt.yscale('ln')

plt.show()
1654692864566.png

接下来

  • 线性相关探索
  • 线性回归/单变量一次方回归
  • 多元多次方回归
  • ...
Legends never die.
Copyright © 2024 Hirsun