Definition
大约 4 分钟
Definition
Joint Distribution

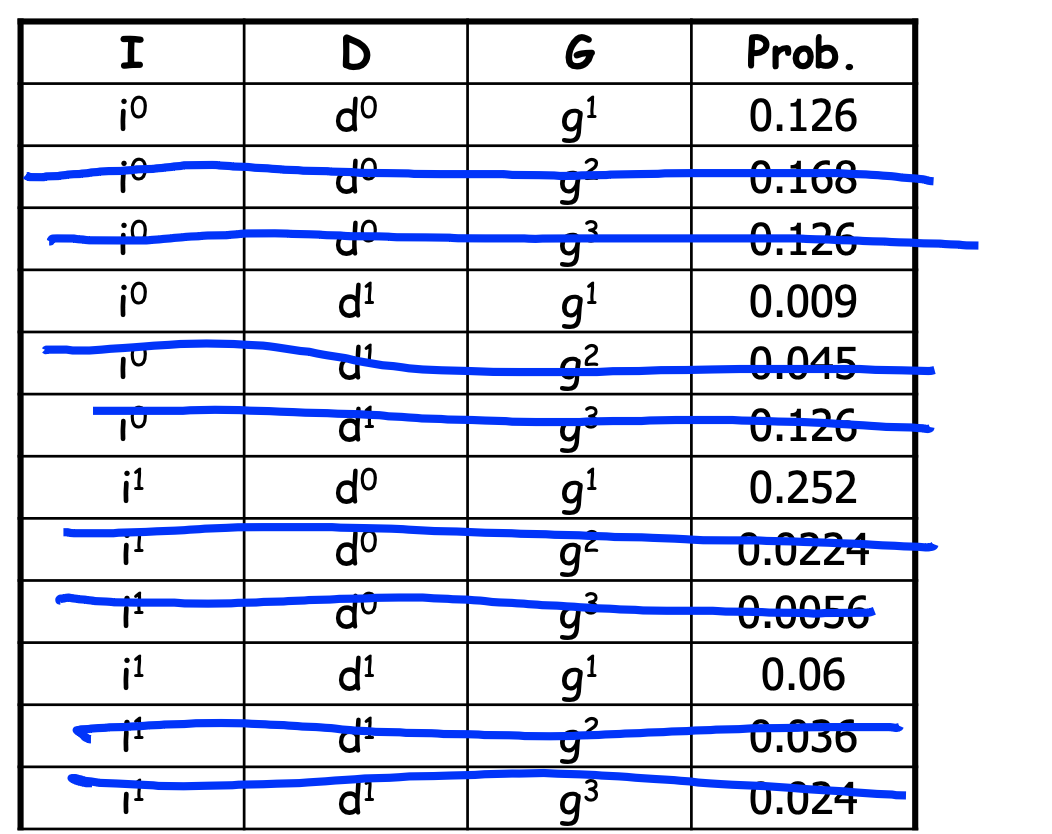
对于这三个变量,这个表描述了他们的联合概率分布。
Reduction
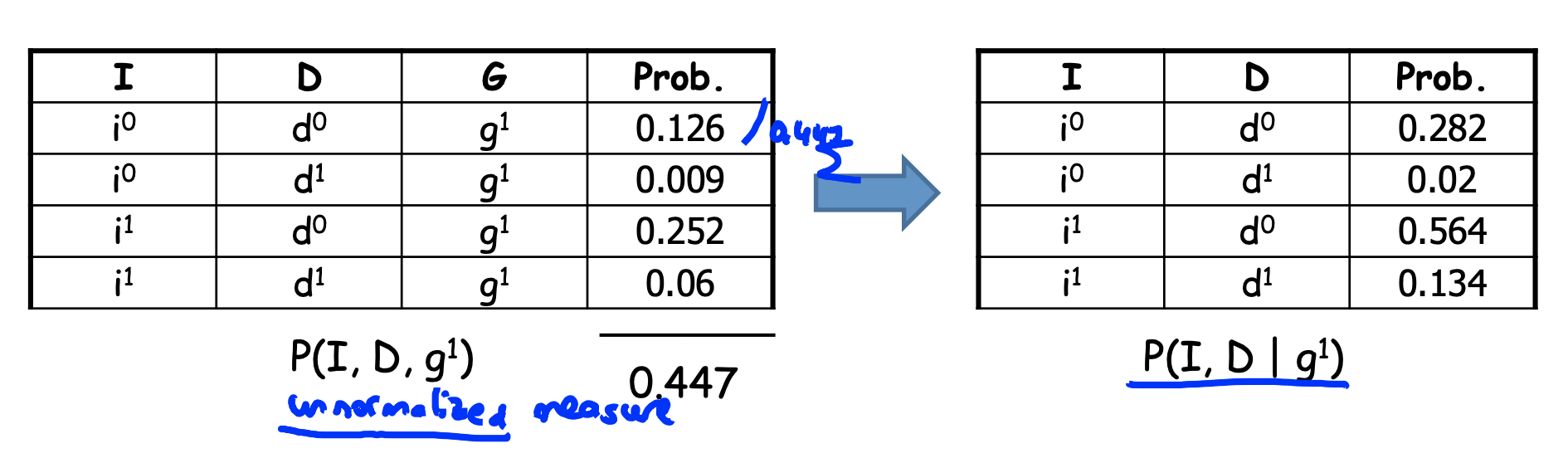
如果基于一个条件:condition on g = g1,删除无用信息,如下,这个过程成为 reduction
之后进行归一化(a joint distribution is a factor)
Marginalization
所谓边际化,即去除一个变量的影响。

通过求和可知。
Factors
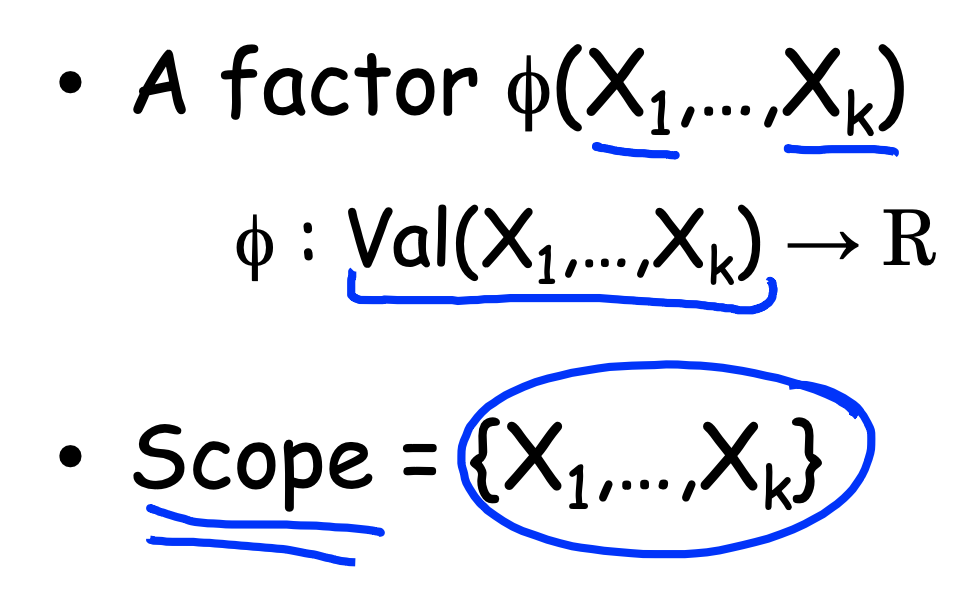
A joint distribution is a factor
Conditional Probability Distribution
除了上面是联合分布因子,还有 Conditional Probability Distribution (CPD)「条件概率分布」

每一行的加和都是1。
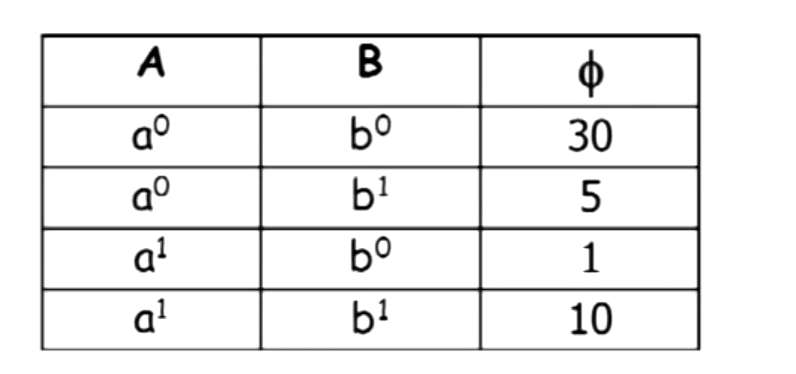
General factors
这也是一种因子,尽管输出值不是在0-1之间。因为因子比一定是概率相关的。
Factor Operations
因子是因子,概率是概率。因子之间的运算和概率无关。
Factor Product
因子之间可以做乘积。即把两个表格乘起来。
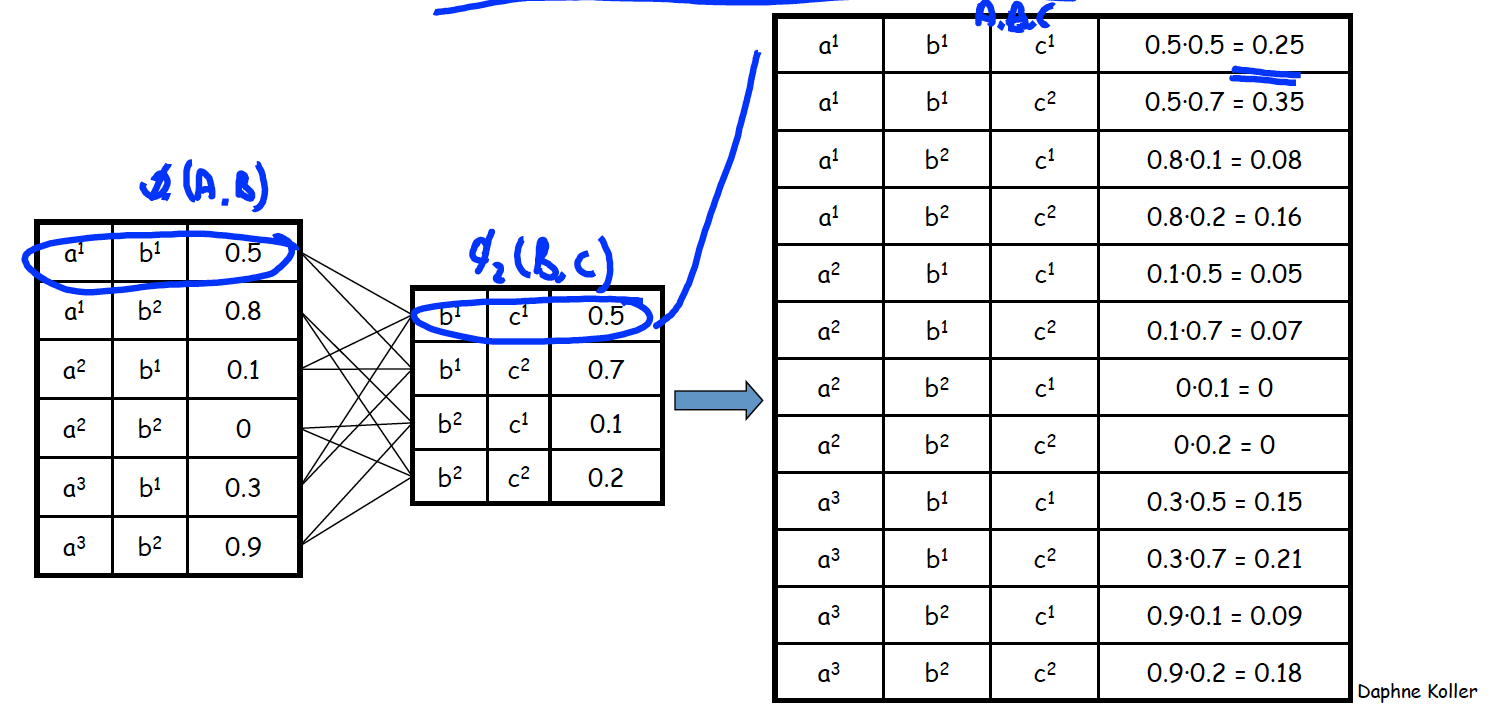
Factor Marginalization
和概率中的边际化操作很相似。
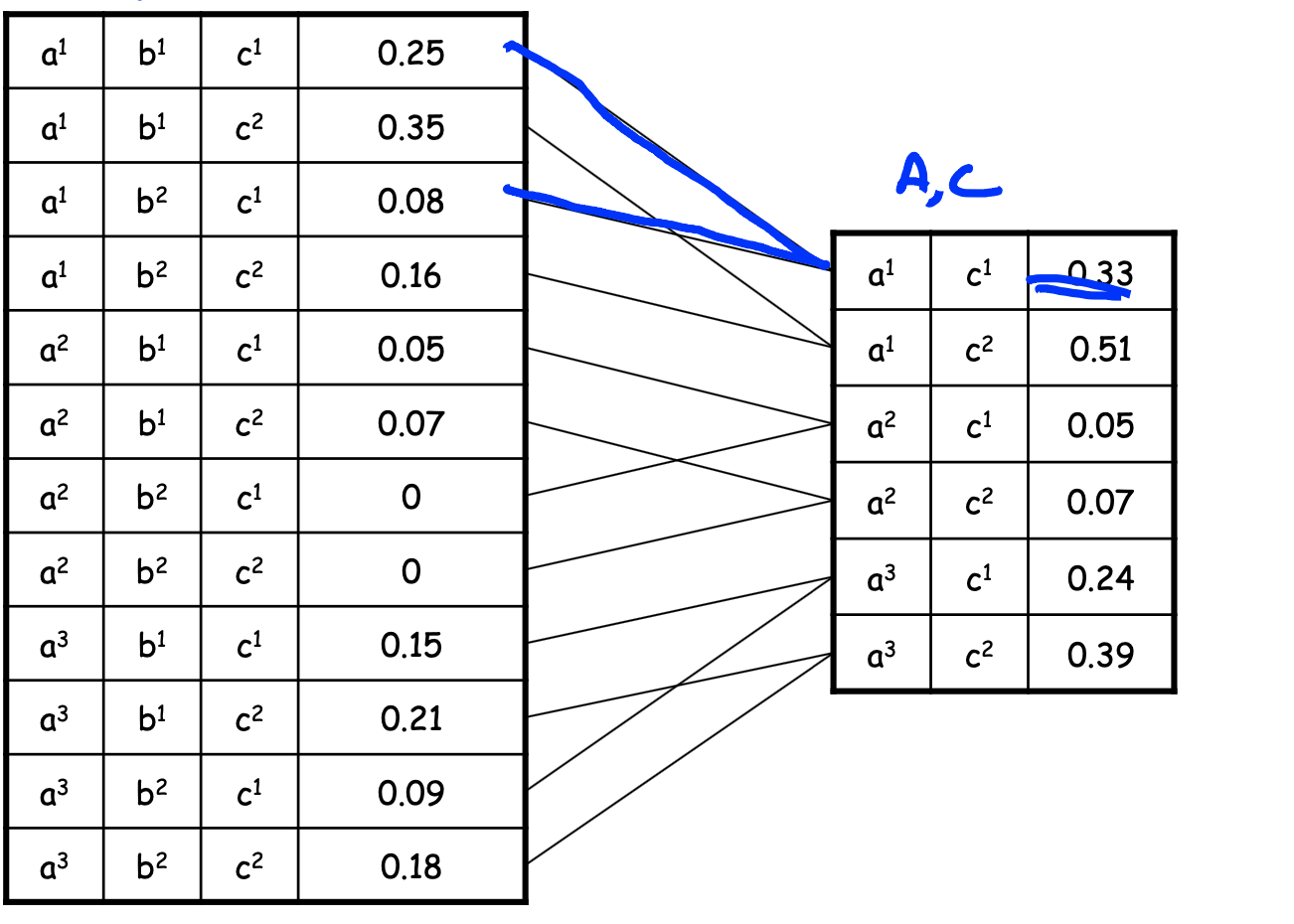
Factor Reduction
和概率中的 Reduction 操作很相似。
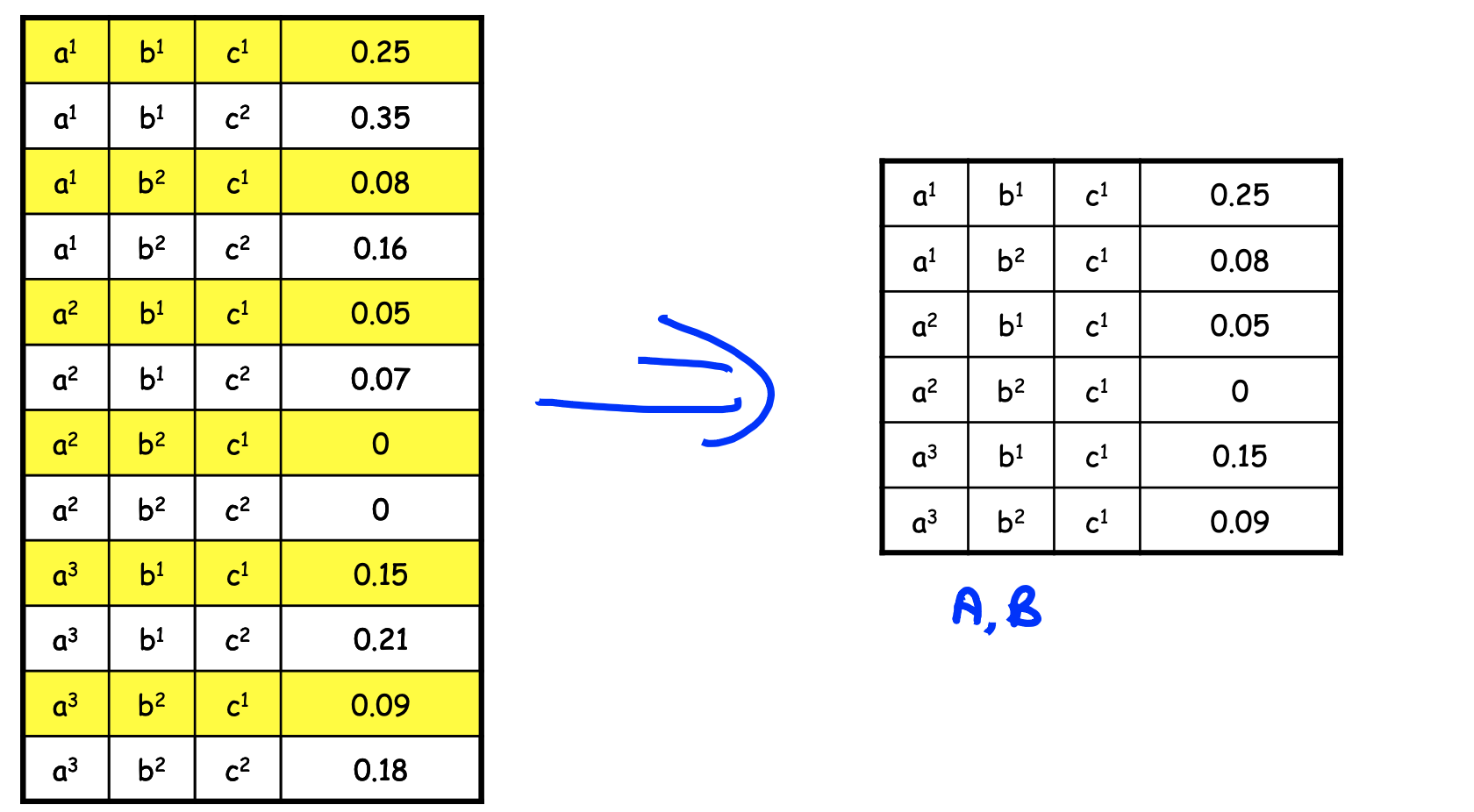
Why factors
我们发现因子是帮助我们定义概率分布和高维空间的重要概念。我们如果要定义一个非常大的概率分布,包含N个随机变量,可以通过把小的定义域的因子乘在一起,来定义高维的概率分布。也可用因子的计算来推导概率。