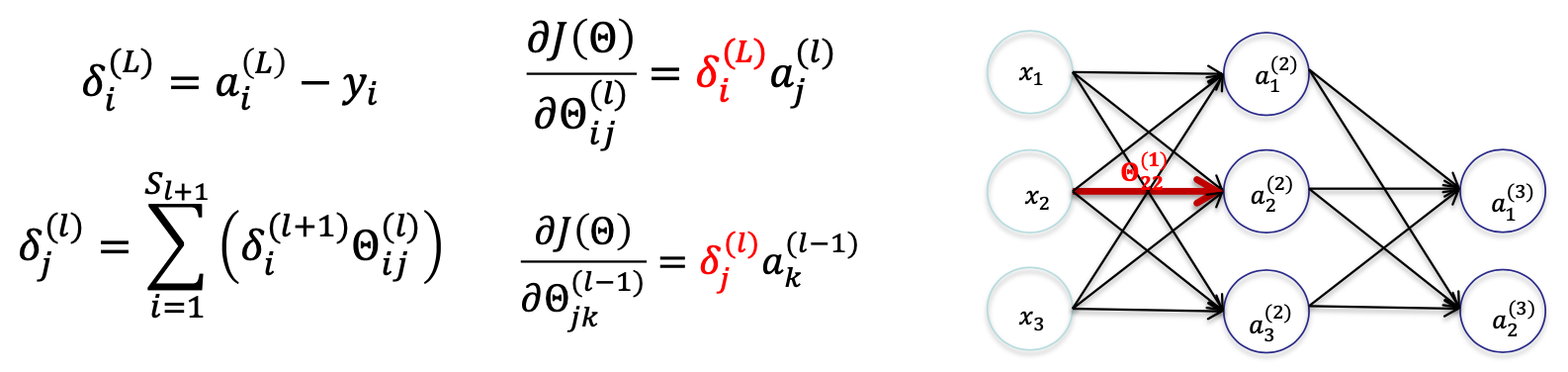BackPropagation
「逆向参数调整法」
Task Setting
- ai(j) : output of unit 𝑖 at layer 𝑗 「j 层 i 项」
- ai(1) = xi 「1 层 i 项」-> 第 i 个输入特征
- θki(j) : weight on link from ai(j) 「j 层 k 项」to ak(j+1) 「j +1 层 i 项」
考虑该神经网络 N,假设激活函数为 g
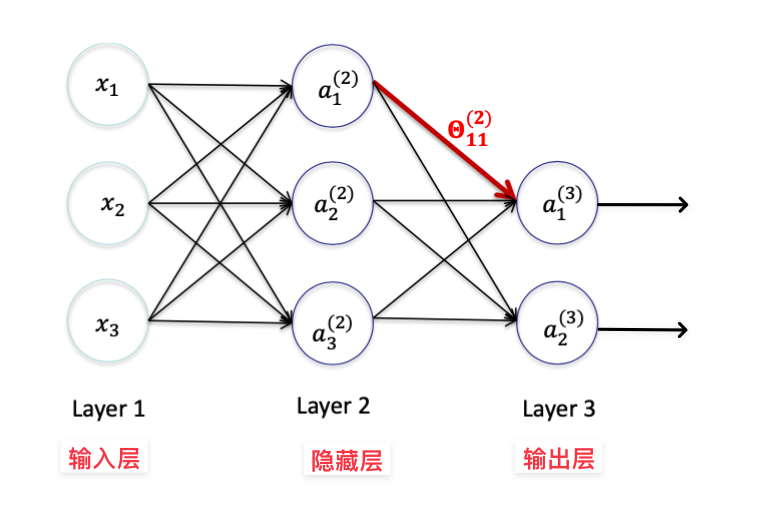
则有
- a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
- a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
- a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
Cost Function
神经网络的训练目标是最小化 总误差函数「代价函数」 E(w),其中 w 表示神经网络的所有权重和偏置。
总误差函数可以根据具体的问题而不同,常见的包括均方误差、交叉熵等。
为了简化任务,假设 神经网络 N 以使用 均方误差+线性神经元,且
- 有 K 个神经元输出,一个样本向量输入
- 输出层中,第 k 个神经元的预期结果为 yk
- 输出层中,第 k 个神经元的实际输出结果为 hΘ(x)k
J(θ)=21k=1∑K(hΘ(x)k−yk)2
其中
- J(θ) 是 关于 hΘ(x)k 的函数
- 在 xk 和 yk 已知的情况下,hΘ(x)k 是关于 θi 的函数
因此 J(θ) 是关于 θi 的函数,应当不断调整每个 θi 的值,使用梯度下降找到 J(θ) 的最小值。这需要对每个 θi 求偏导数。
提示
对于 m 个样本,L = l + 1 层的神经网络, J(θ) 应该是
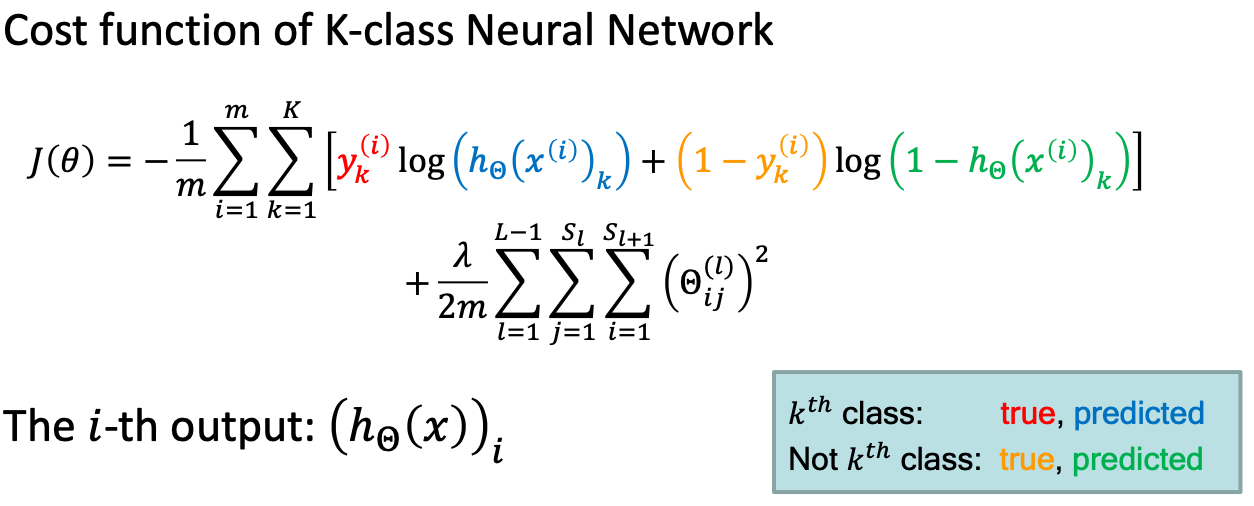
J(Θ)=2m1i=1∑mk=1∑SL(hΘ(x(i))k−yi)2+2mλl=1∑L−1j=1∑Sli=1∑Sl+1(Θij(l))2
此外,交叉熵误差函数在分类问题中应用广泛
Find Gradient
继续研究神经网络 N 。由于 神经网络 N 中输出结果不只有一个,因此应当对代价求和,即
J(Θ)=21((hΘ(x))1−y1)2+21((hΘ(x))2−y2)2
反向传播算法的核心是计算误差项 δi(l),它代表着第 l 层第 i 个神经元对损失函数的贡献。**然后根据误差项来更新权重和偏置。**以下是从输出层开始逐层计算误差项的过程。因此我们设定
- yp 表示输出层第 p 个神经元的输出值
- δp(j) 记作 第 j 层 p 个 神经元的输出结果 对 最后一层的输出神经元的差值的贡献值
- 如果 j = L -1 是最后一层,则 δi(L−1)=ai(L−1)−yi
- 否则为权重加和,需要通过递归计算,即 δj(l)=∑i=1Sl+1(δi(l+1)Θij(l))
易错警告
- 所有的计数,都要从1开始,而不是0
- 一共有 L = l + 1 层神经网络,而不是 l 层
- 考虑权重 θ 时
- 输入层的输出有权重,所以存在 $
- 输出层没有权重,因此不存在 θp(L)
- 角标 j 的层关系,指的是当前层和下一层 j + 1
- 考虑差值贡献 δ 时
- 输入层没有差值贡献,所以不存在 δp(1)
- 输出层有差值贡献,所以存在 δp(L)
- 每一层的贡献值的加和都是 J(Θ)
- 角标 j 的层关系,指的是当前层和上一层 j - 1
Delta L
神经网络 N 中, l = 2
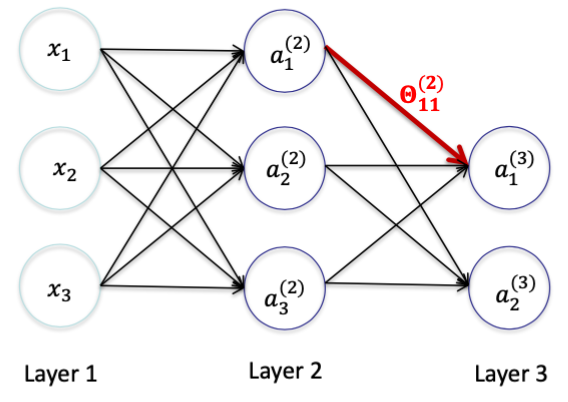
对 θ11(2) 求偏导数,可知
∂Θ11(2)∂J(Θ)=∂Θ11(2)∂21((hΘ(x))1−y1)2+0=∂a1(3)∂21(a1(3)−y1)2∂Θ11(2)∂a1(3)=(a1(3)−y1)⋅∂Θ11(2)∂a1(3)=(a1(3)−y1)⋅∂Θ11(2)∂(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))=(a1(3)−y1)a1(2)=δ1(3)a1(2)
相关信息
在这里,a1(2) 是关于 x 的函数。
Delta L - 1
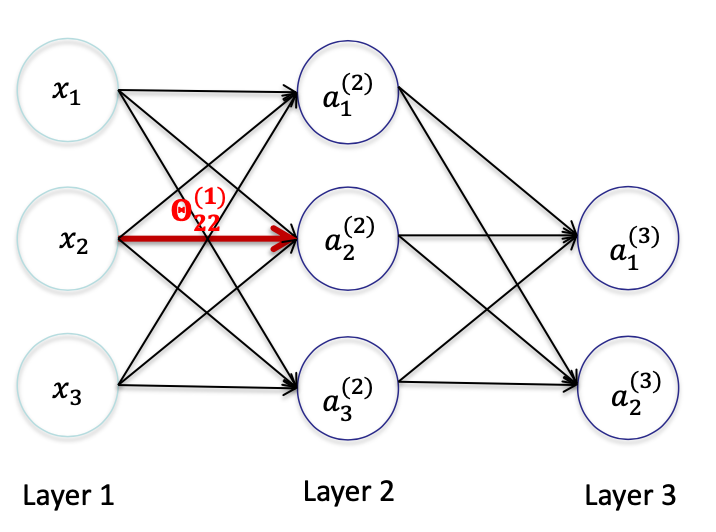
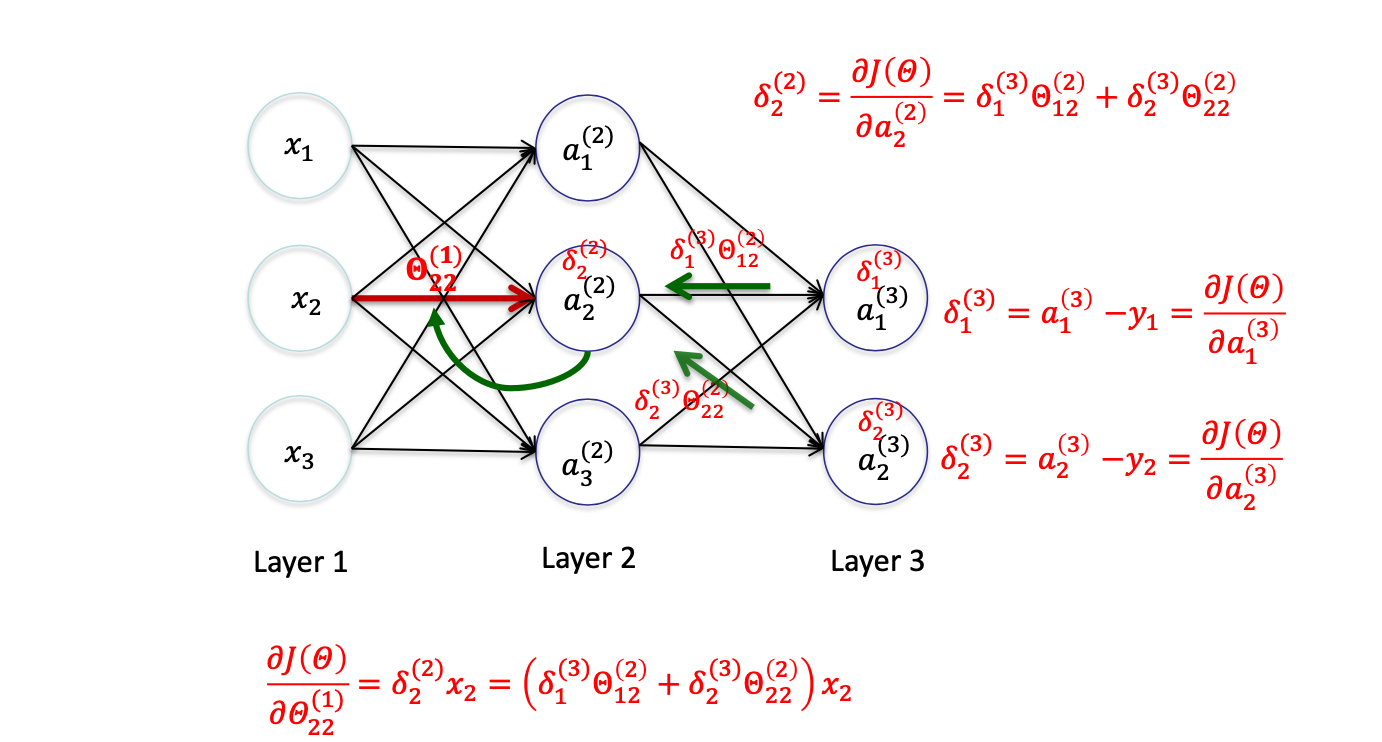
对 θ22(1) 求偏导数,可知
∂Θ22(1)∂J(Θ)=∂Θ22(1)∂21(a1(3)−y1)2+∂Θ22(1)∂21(a2(3)−y2)2=∂a1(3)∂21(a1(3)−y1)2∂Θ22(1)∂a1(3)+∂a2(3)∂21(a2(3)−y2)2∂Θ22(1)∂a2(3)=(a1(3)−y1)∂Θ22(1)∂a1(3)+(a2(3)−y2)∂Θ22(1)∂a2(3)=(a1(3)−y1)∂Θ22(1)∂(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))+(a2(3)−y2)∂Θ22(1)∂(Θ20(2)a0(2)+Θ21(2)a1(2)+Θ22(2)a2(2)+Θ23(2)a3(2))=(a1(3)−y1)∂a2(2)∂(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))⋅∂Θ22(1)∂a2(2)+(a2(3)−y2)∂a22∂(Θ20(2)a0(2)+Θ21(2)a1(2)+Θ22(2)a2(2)+Θ23(2)a3(2))⋅∂Θ22(1)∂a2(2)=((a1(3)−y1)Θ12(2)+(a2(3)−y2)Θ22(2))⋅∂Θ22(1)∂a2(2)=((a1(3)−y1)Θ12(2)+(a2(3)−y2)Θ22(2))⋅∂Θ22(1)∂(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)=((a1(3)−y1)Θ12(2)+(a2(3)−y2)Θ22(2))x2=(δ1(3)Θ12(2)+δ2(3)Θ22(2))x2
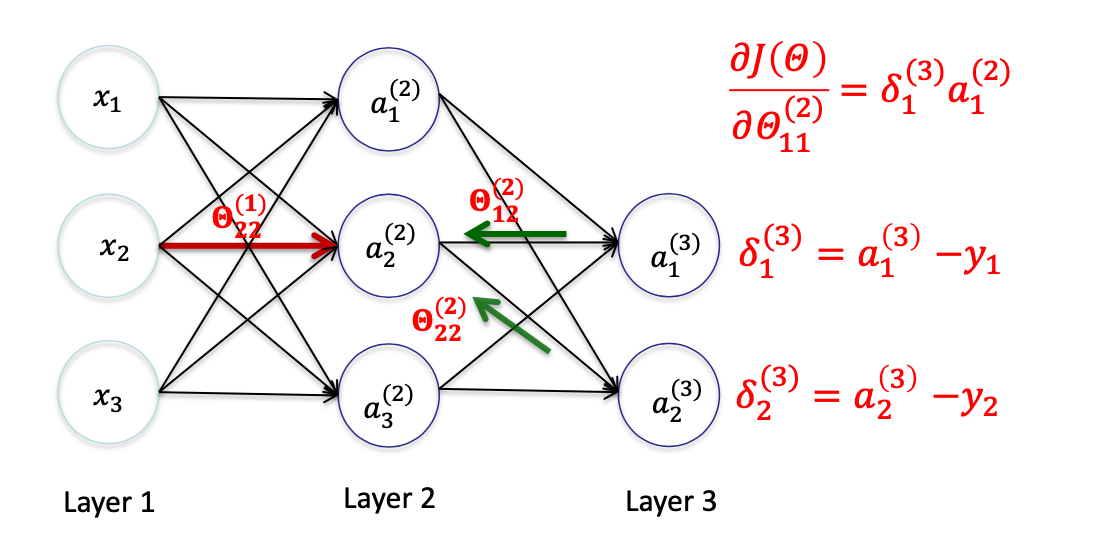
∂Θ22(1)∂J(Θ)=((a1(3)−y1)Θ12(2)+(a2(3)−y2)Θ22(2))x2=(δ1(3)Θ12(2)+δ2(3)Θ22(2))x2,该结果可记作 δ2(2)x2
Summary
对于 L 层 和 L- 1 层
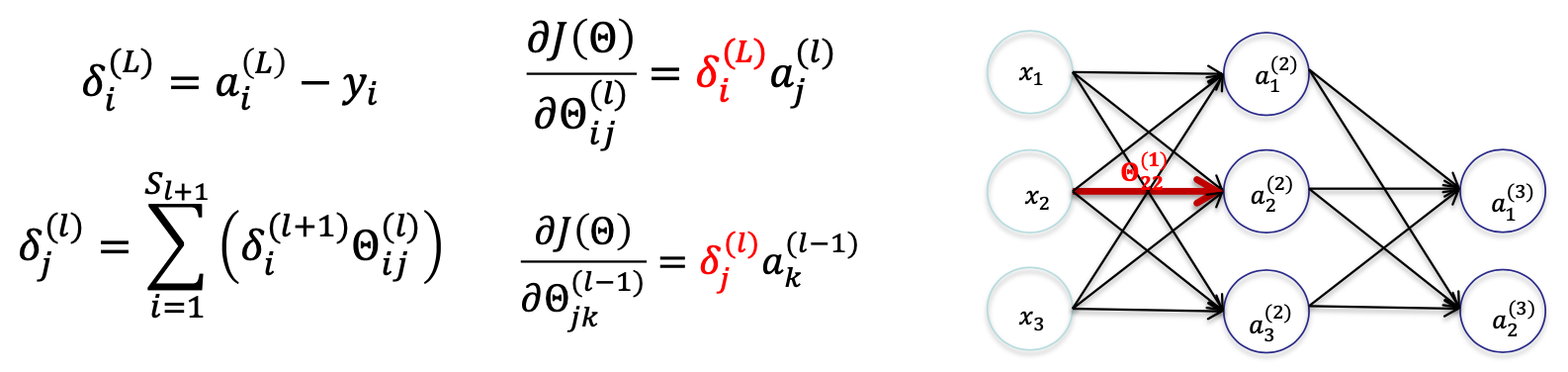
Delta L - n: 动态规划思想
Directly Applying Gradient Descent is Expensive!
因此,不妨先把算出来的 δ 值存起来,以便前面的神经元直接使用。
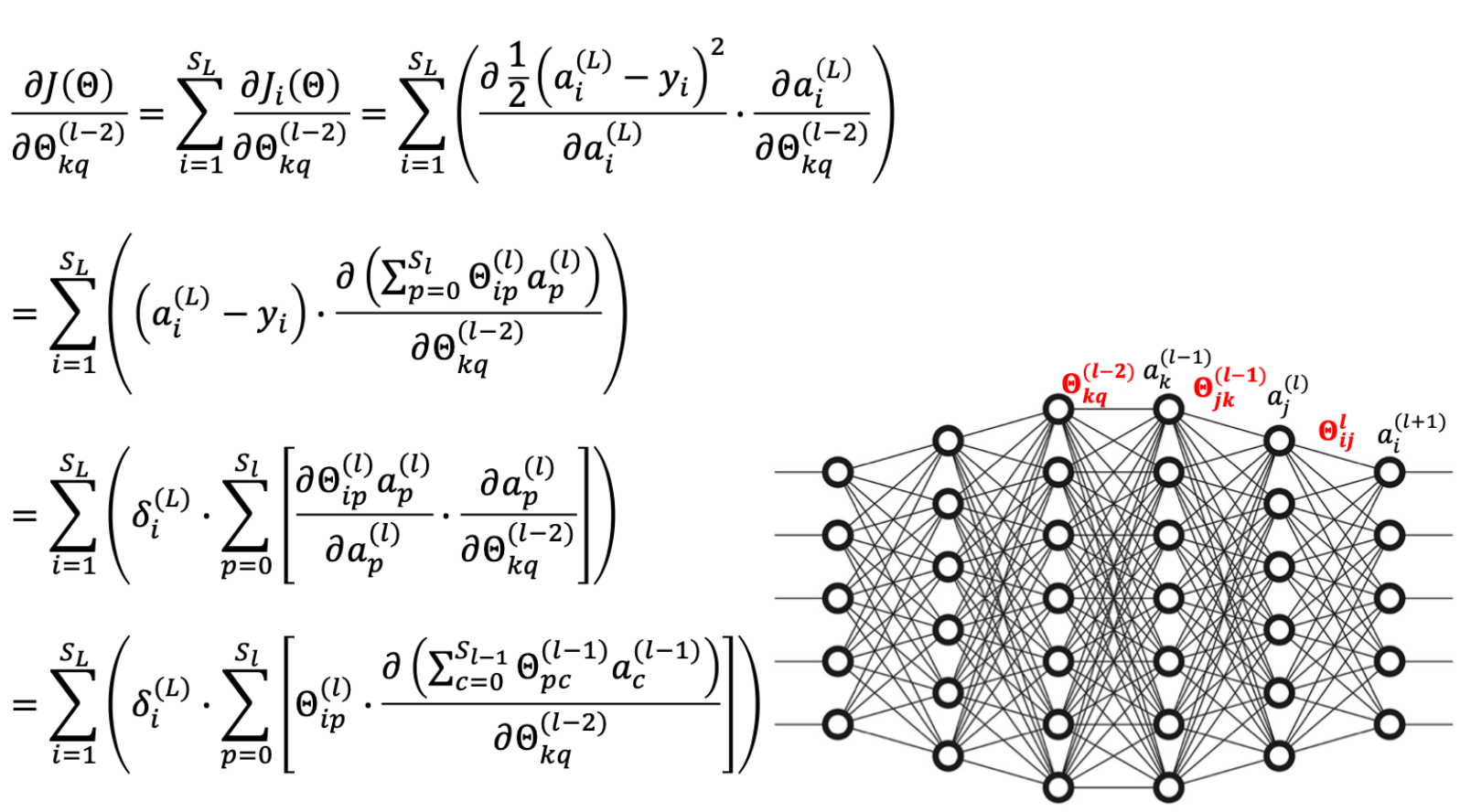
Gradient Derivati
整个过程应当是,先正向传播,再反向传播。因此初始时应随机指定每个神经元权重的值。反向传播如扩散一般。
 1678180461969.png
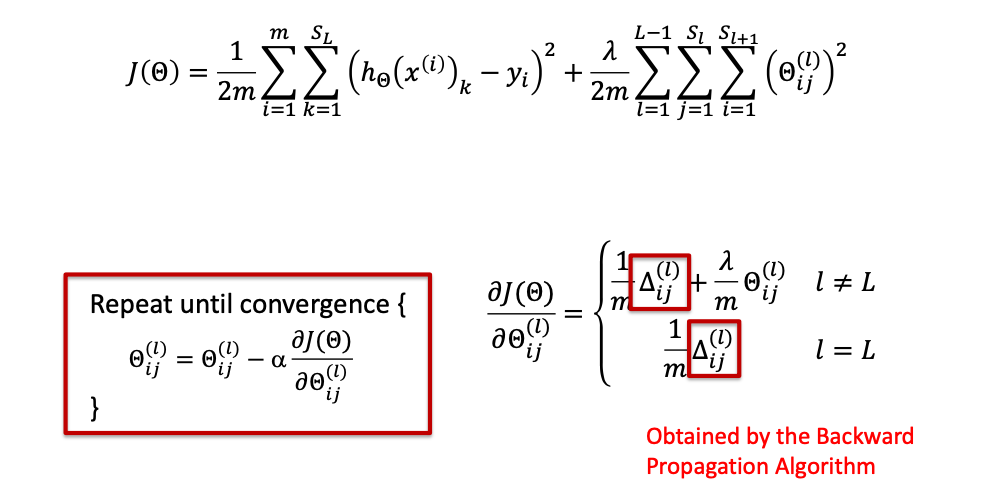
1678180461969.png Back Propagation Algorithm
 1678180619317.png
1678180619317.png Gradient Descent Algorithm
 1678180996838.png
1678180996838.png再次提醒
输出层没有权重,因此不存在 θp(L) 。如果非要说有,那就是 1。一般情况下,L 是不会取到 L 的。
Implementation Detail
- 对网络中的 初始权重 Θ 进行随机化 非常重要
- 不能有统一的初始权重,否则所有的更新都将是相同的,网络将不会学到任何东西。
Ref