Neural Network

1677428364696.png

• 非常强大，但由于其复杂性和大量的计算资源而被抛弃了几十年。
• 由于更高的计算能力（数据中心）和更多的训练实例（大数据），这几年又重新出现。

Inspired by Human Brain

• 我们的大脑有很多神经元连接在一起
• 人脑是一个由 100 个 B 节点和 700 个 T 边组成的图/网络

神经元之间的连接强度代表长期的知识。

1677421301990.png

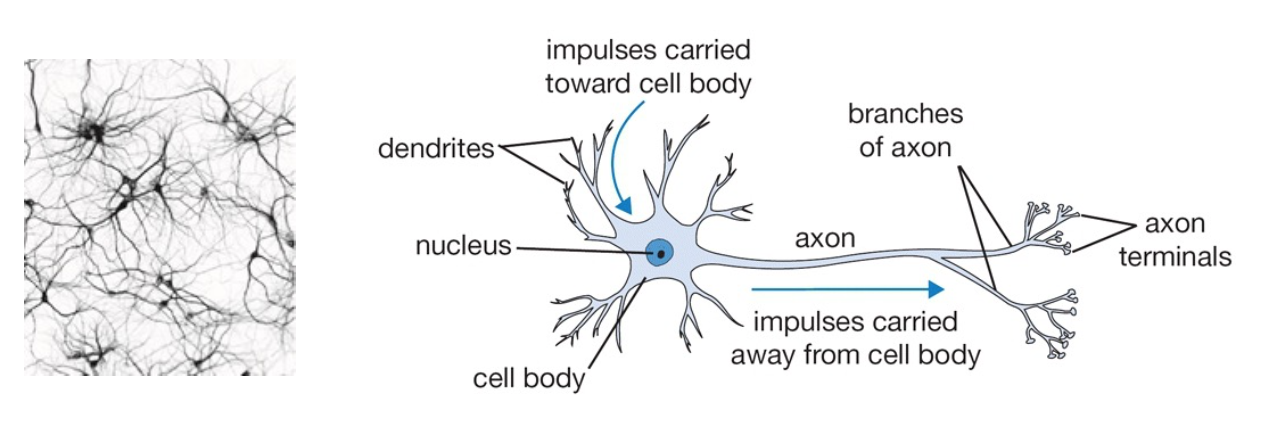
• 它从您的输入特征中学习新特征。
• 它的架构基于我们的大脑结构。
• 一个神经元的轴突末端与另一个神经元的树突相连，这就构成了一个相当复杂的神经网络。

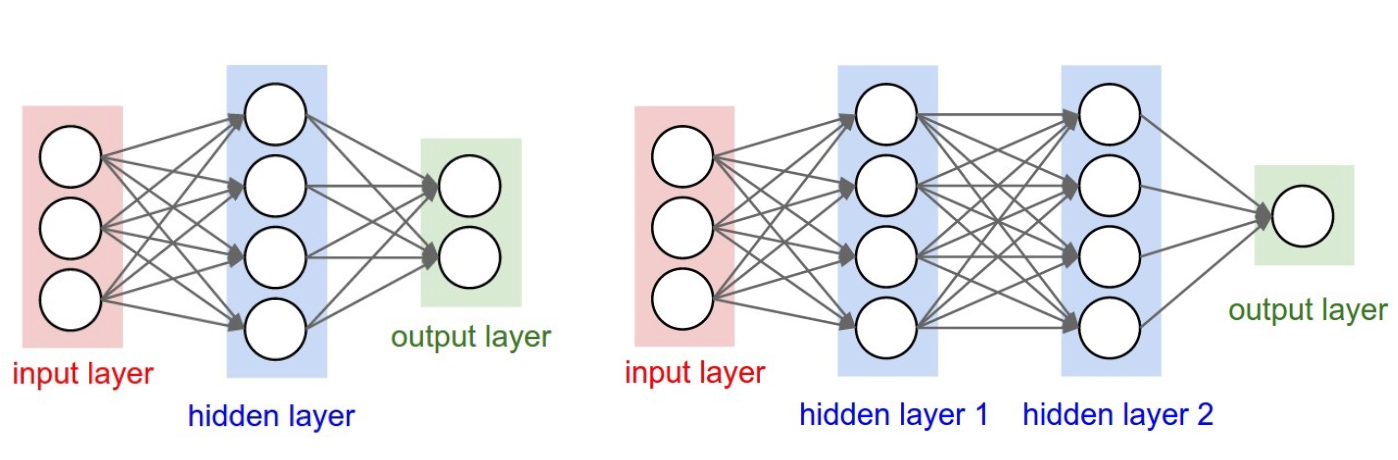
Artificial Neuronal Networks

ANN「人工神经元网络」

1678081999133.png

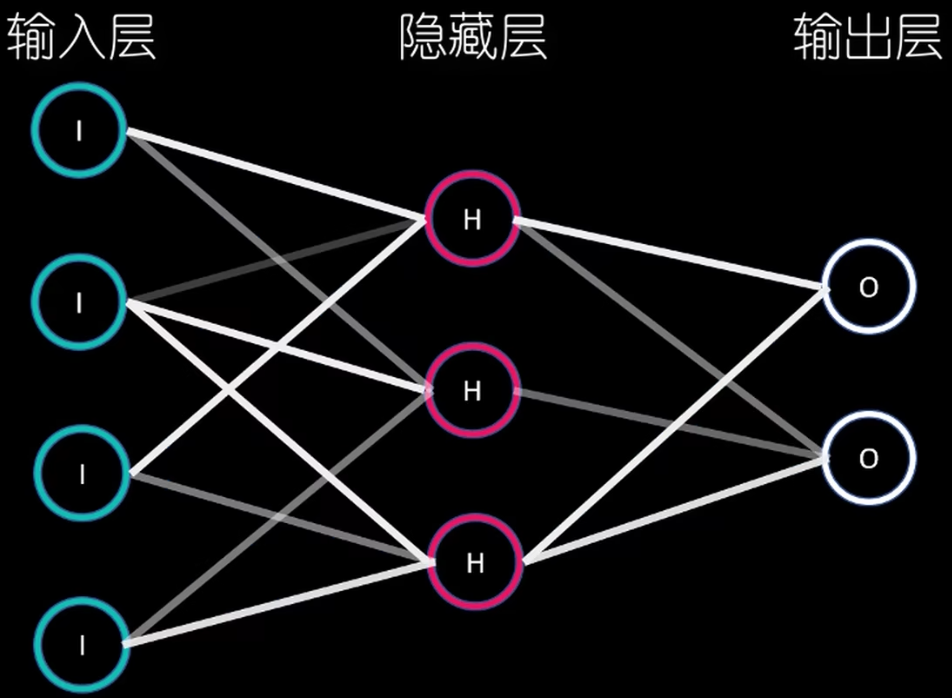
Model Structure

• 不同层的神经元按照不同的权重设置而连接

• 输入层的神经元仅仅起到传递数据的作用

  • 他们将配置的权重传导至隐藏层的相应的神经元

• 输入层的神经元仅负责输出

1678082298874.png

The Artificial Neuron

前面介绍说有三种人造神经元，就隐藏层「感知层/Perception」的神经元而言，

• 对于每一个神经元，其信号强度由上层传输的加权和所决定。
• 激活函数「Activation Function」会将该输入信号转化为该神经元的输出值，最终通过输出层产生结果。

从外部来看，一个神经元就像这样一个橙色的圈。

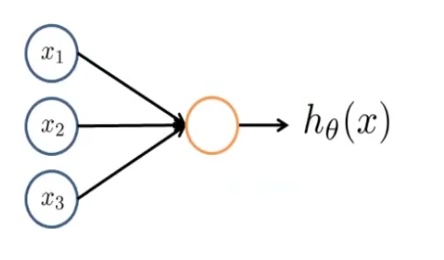
• 𝑥_i are input nodes
• h_𝜃(𝑥) is the output
• 接受输入的节点代表神经元的主体

以逻辑神经元为例。一个隐藏层的神经元需要具备以下三个功能

• 接受前神经元的输出做为输入
• 设置并记录每一个前神经元输入值的权重
• 计算 $g\left(x_{i}\right)=\sum_{i=1}^{n} w_{i} x_{i}+b$ 的值
• 将上面的计算结果带入激活函数，得到这个神经元的输出值

1678082652649.png

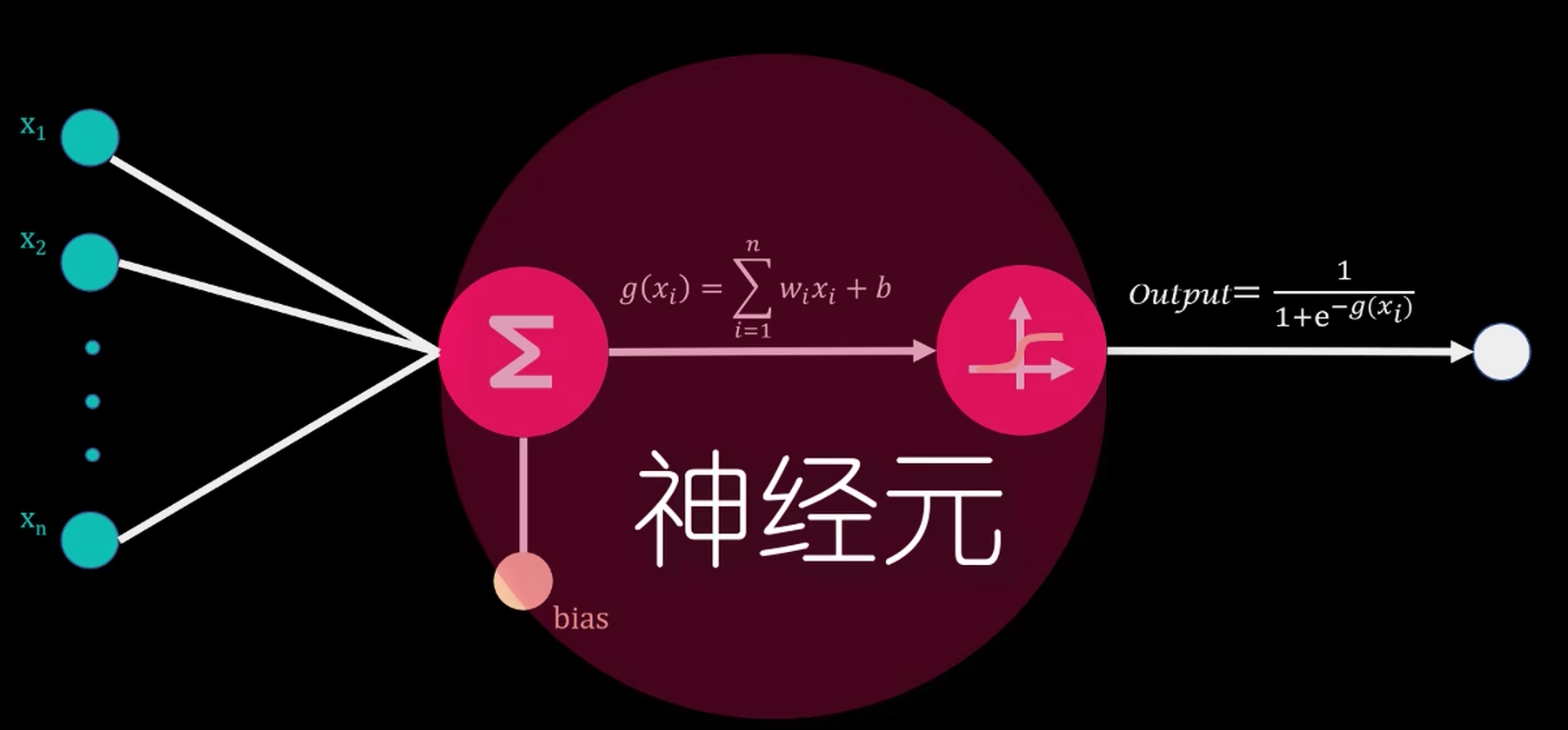
在上图中，激活函数是 Sigmoid 函数。

Bias

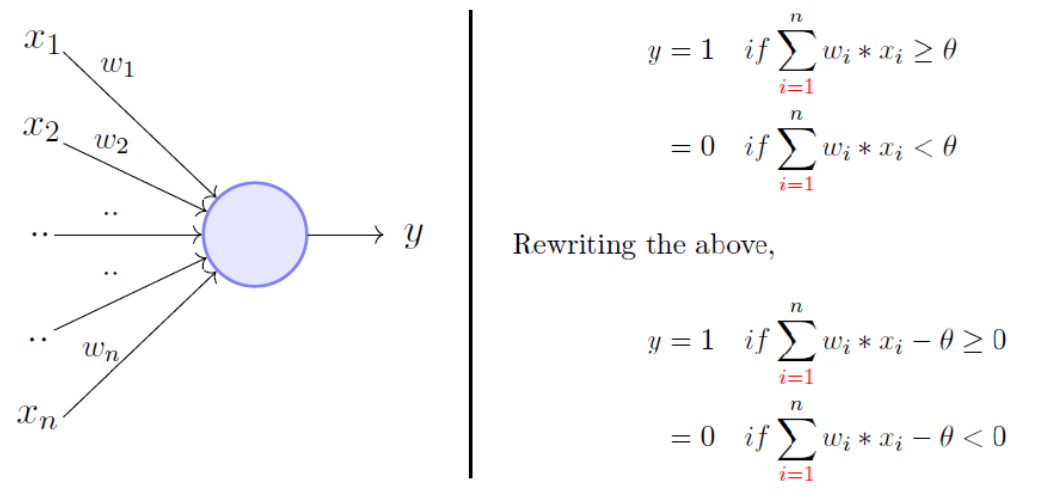
bias 也叫阈值「threshold」。

人造神经元的 bias 是神经元的一个可学习参数，它决定了神经元的激活阈值，也就是神经元在什么样的输入下会被激活。

取输入的加权和，仅当总和大于任意阈值「threshold」时才将输出设置为 1

1677427617932.png

如果是线性神经元，可以这样改写：

1677428022777.png

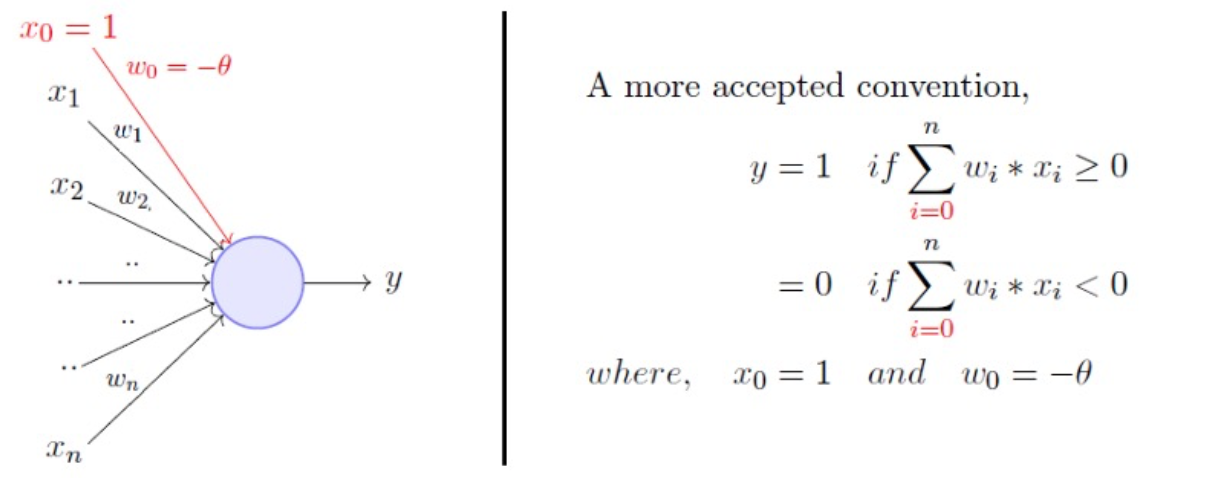
每个线性神经元都有一个 bias 参数。当网络接收到输入信号时，每个神经元的输入信号会与其对应的权重相乘，然后将它们相加，并加上该神经元的 bias。这个结果被送入激活函数中，以产生神经元的输出。

Linear Neuron

线性神经元没有激活函数，或者更准确地说，它们的激活函数是恒等函数，它只是输出神经元输入的加权和加上它的偏差。

985f083de76e0.png

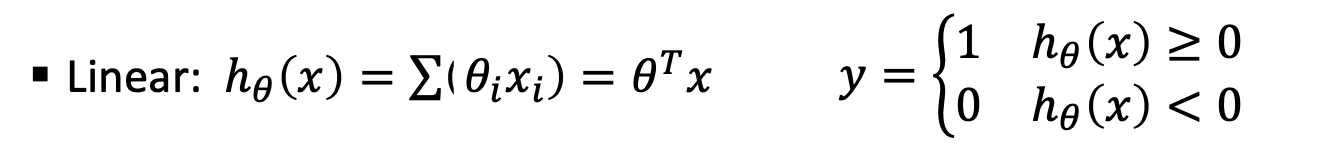
Logistic Neuron

985f083de76e022.png

1677428334419.png

1677428317104.png

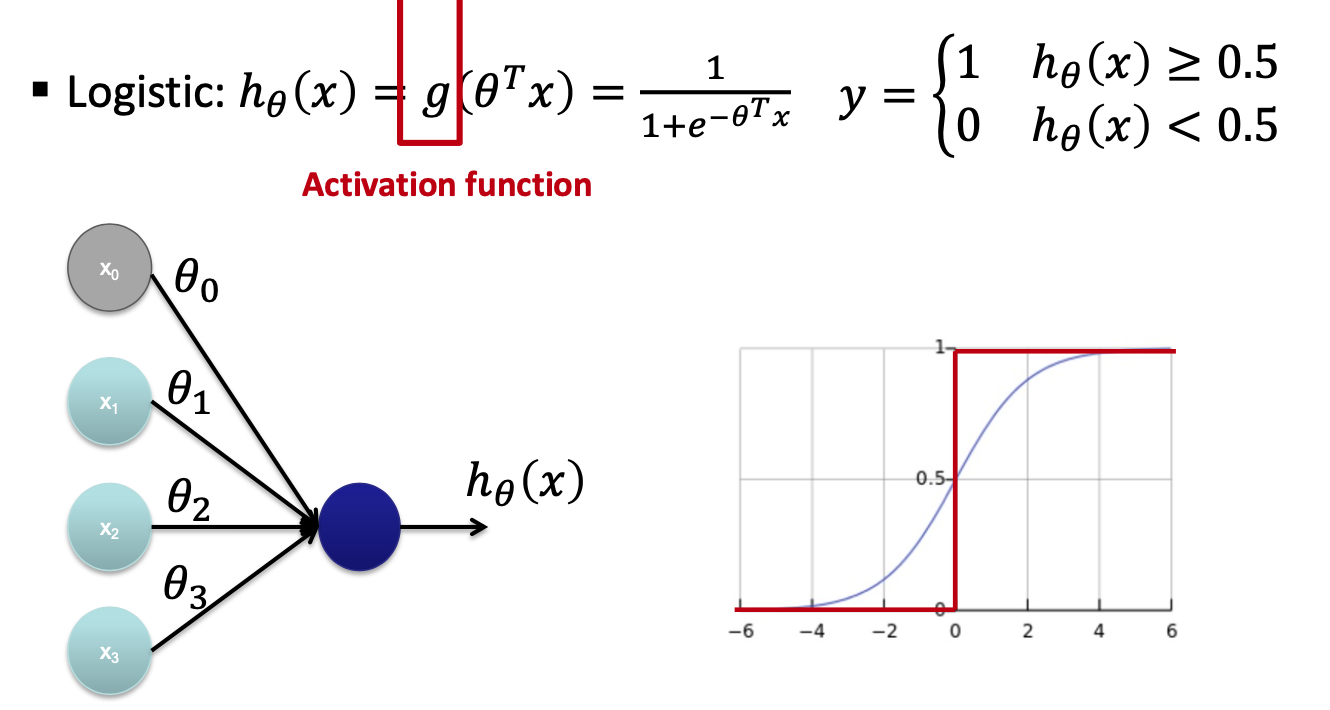
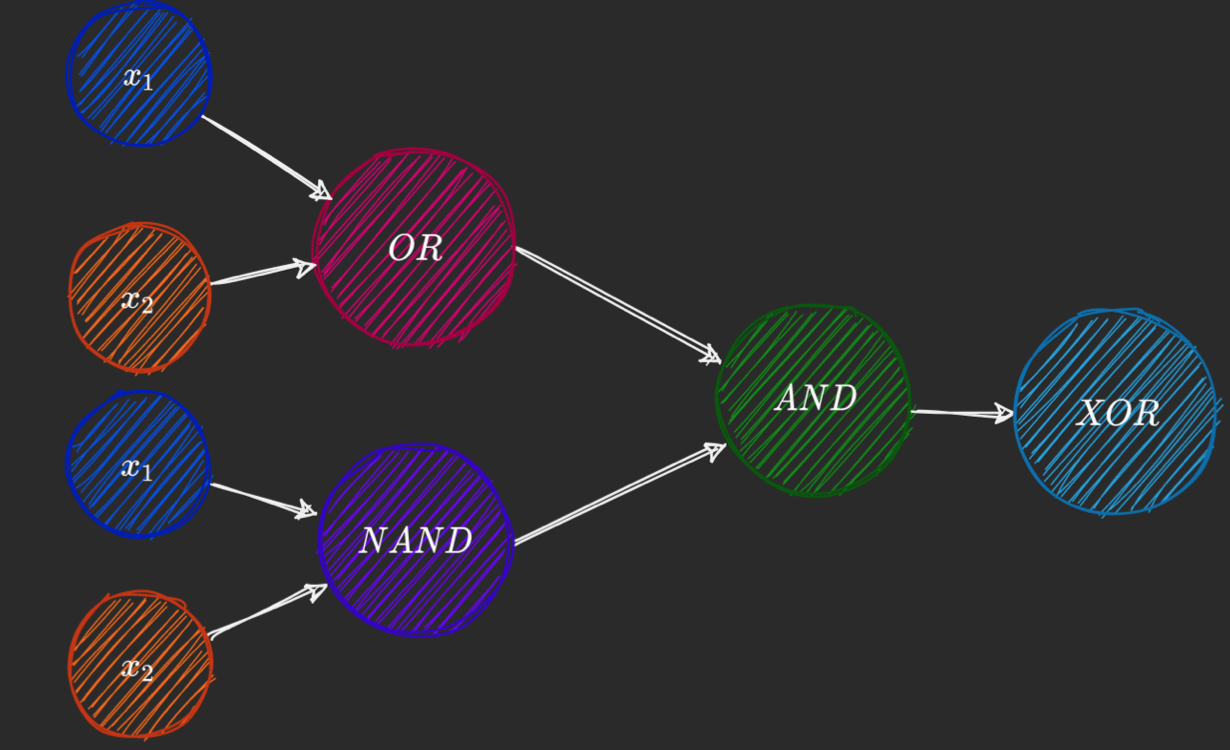
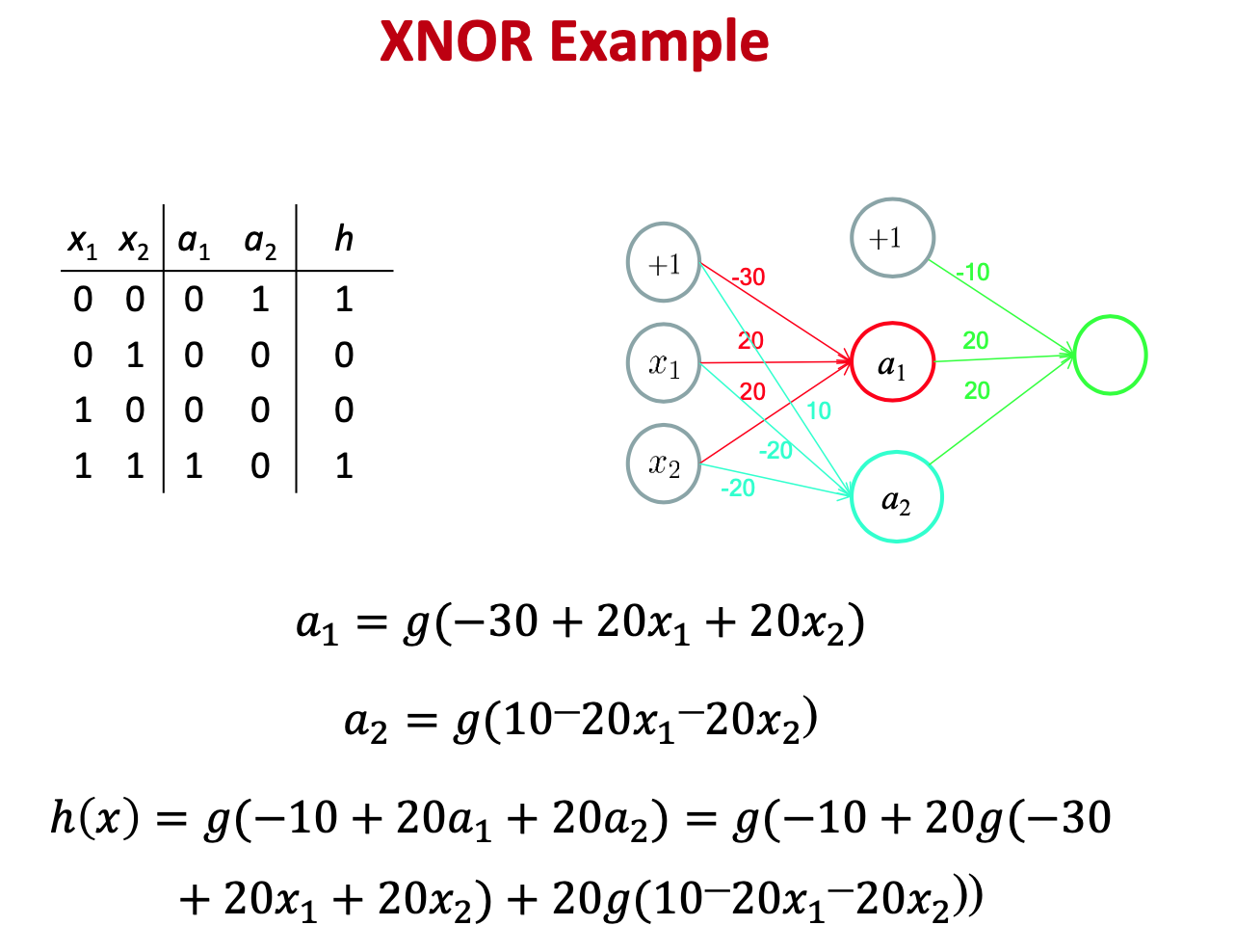
Training Objective

假设这样一个神经网络模型：

• 隐藏层只有一个神经元，且也充当输出层的神经元
• 不考虑 bias

首先随机初始化一个 w1和w2。

1678085301770.png

训练的目标是，通过不断调整 W1 和 W2，让 Y、E 集合的 误差平方和 最小。这个过程需要

• 梯度下降法 Gradient Descent
• 链式法则 Chain Rule

步幅 △w

在步幅函数中，△w 的值前有一个负号，这是由于步幅调整方向和导数值相反。

$$\Delta w_{j}=-\eta \partial S / \partial w_{j}$$

这样来看，新的 $\theta$ = $\theta$ + $\Delta w_{j}$

Ref

• https://www.bilibili.com/video/BV12b4y1X7Wv/?spm_id_from=333.788&vd_source=0c500da69cdb9a3d23c34ee522fb2fab