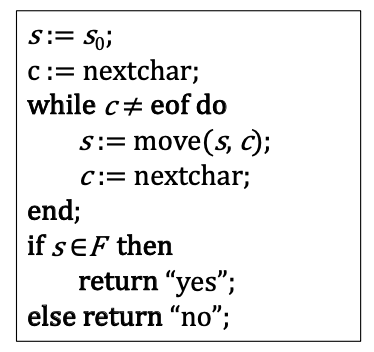Finite Automata
大约 6 分钟
Finite Automata
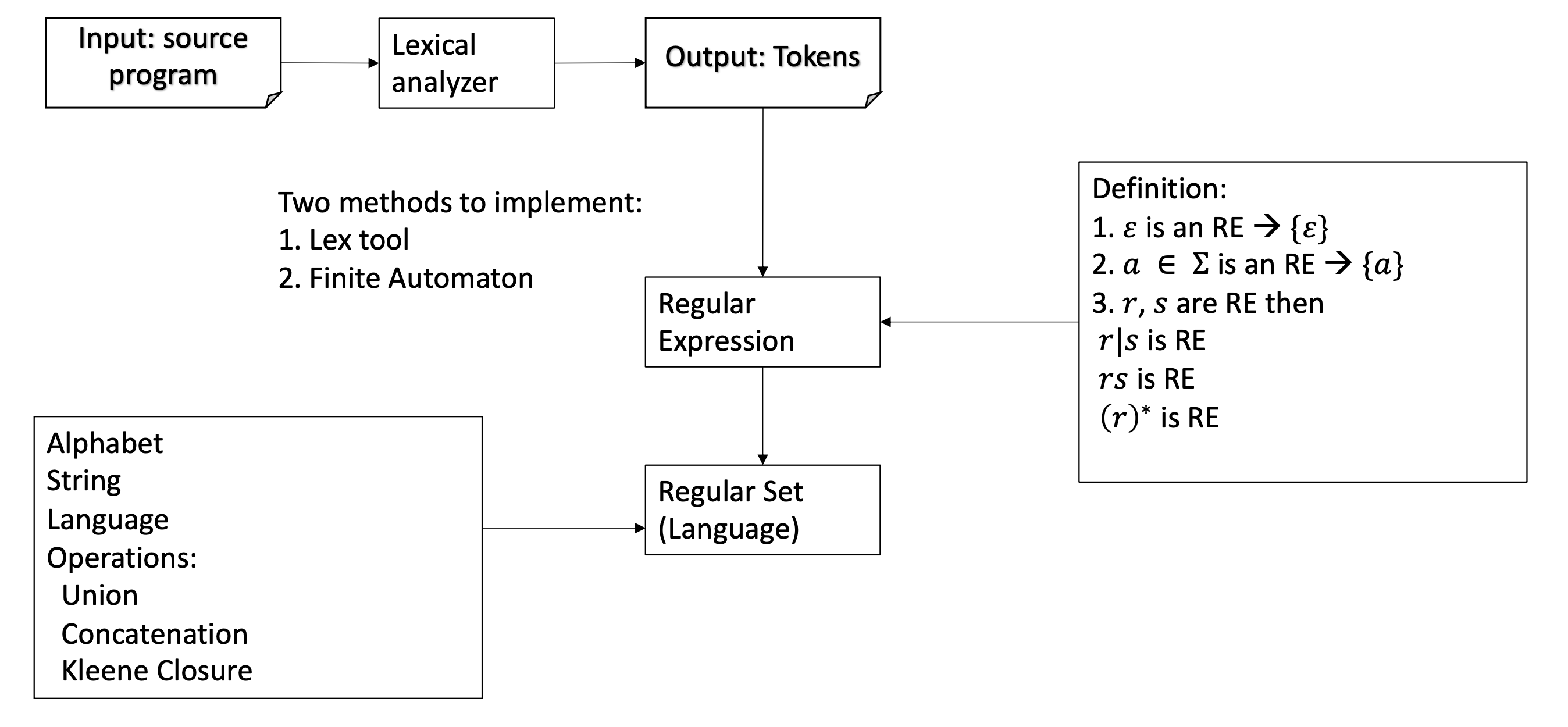
通过放入有限自动机模型来实施正则表达式识别算法。
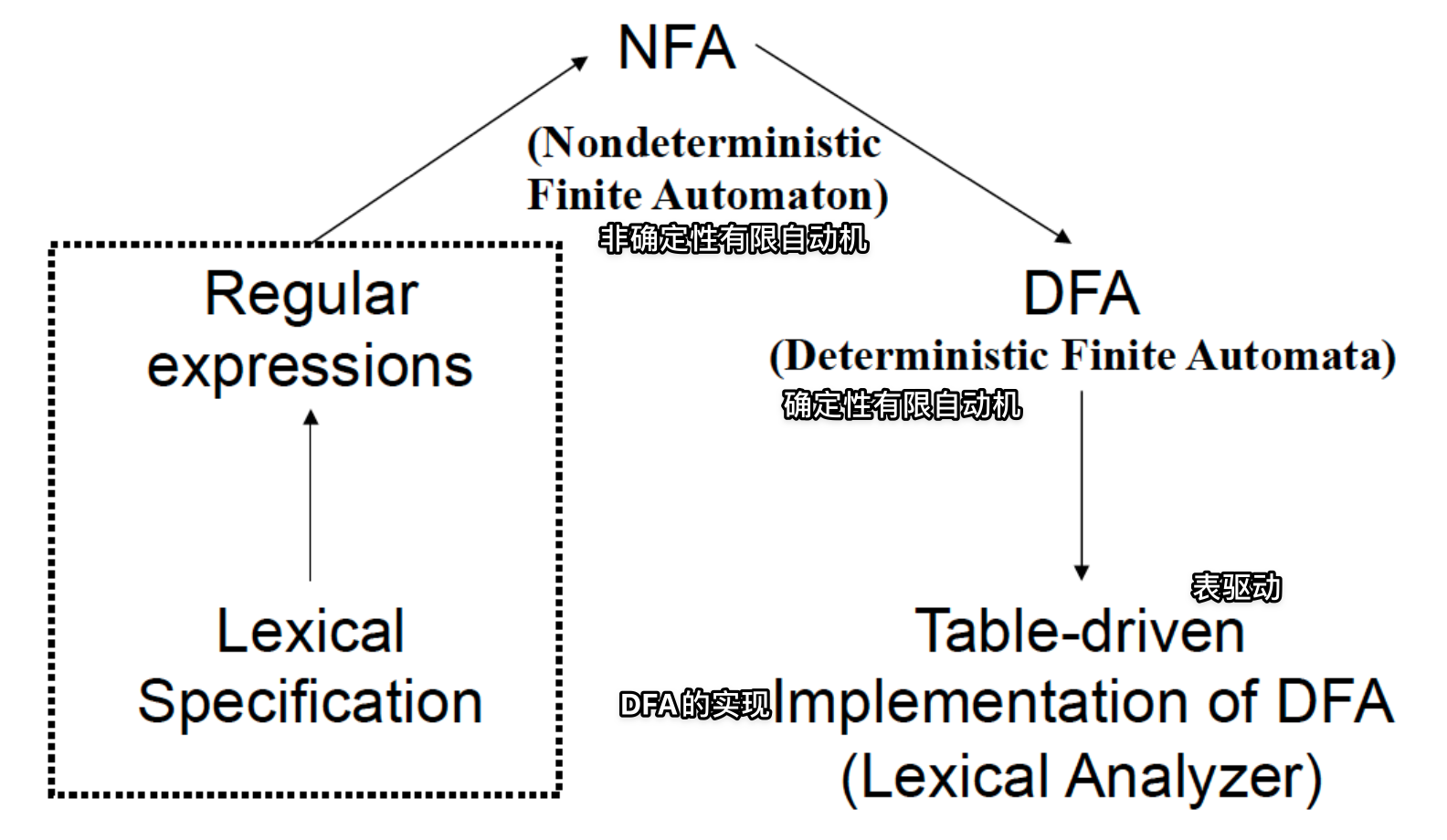
非确定性有限自动机(NFA)
Nondeterministic Finite Automata
非确定性有限自动机 (NFA) 由 5 个组件组成: (Σ, 𝑆, 𝑆0, 𝐹, move).
- Σ is the input alphabet
- 𝑆 is the set of states
- 𝑆0 is the start state
- 𝐹 ⊆ 𝑆 is the set of accepting states「接受状态的集合」
- Move 是将 状态-符号对 映射到 状态集 的 转换函数。
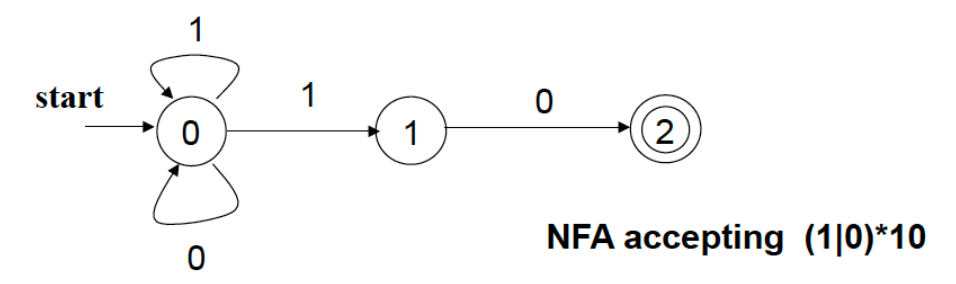
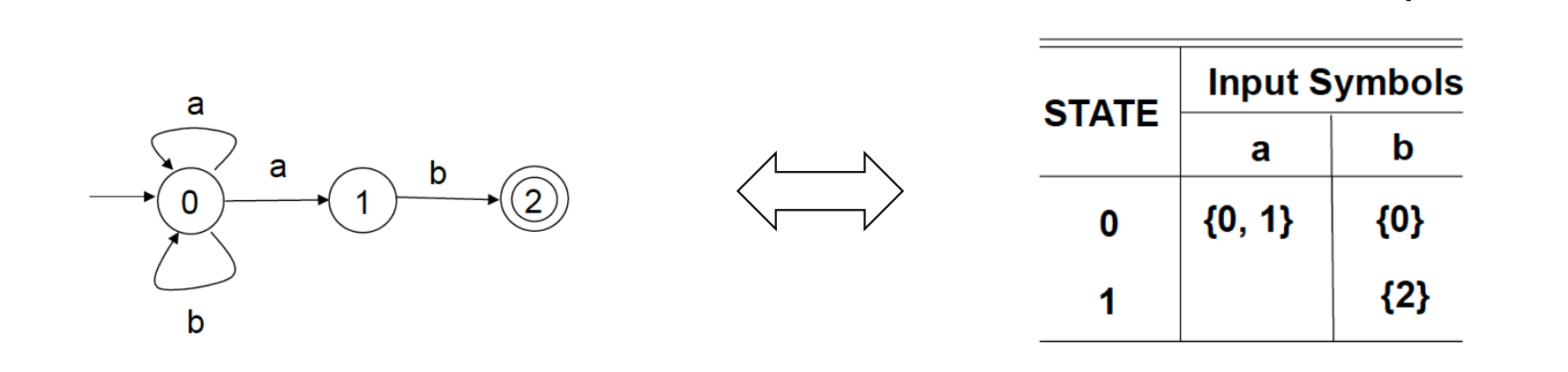
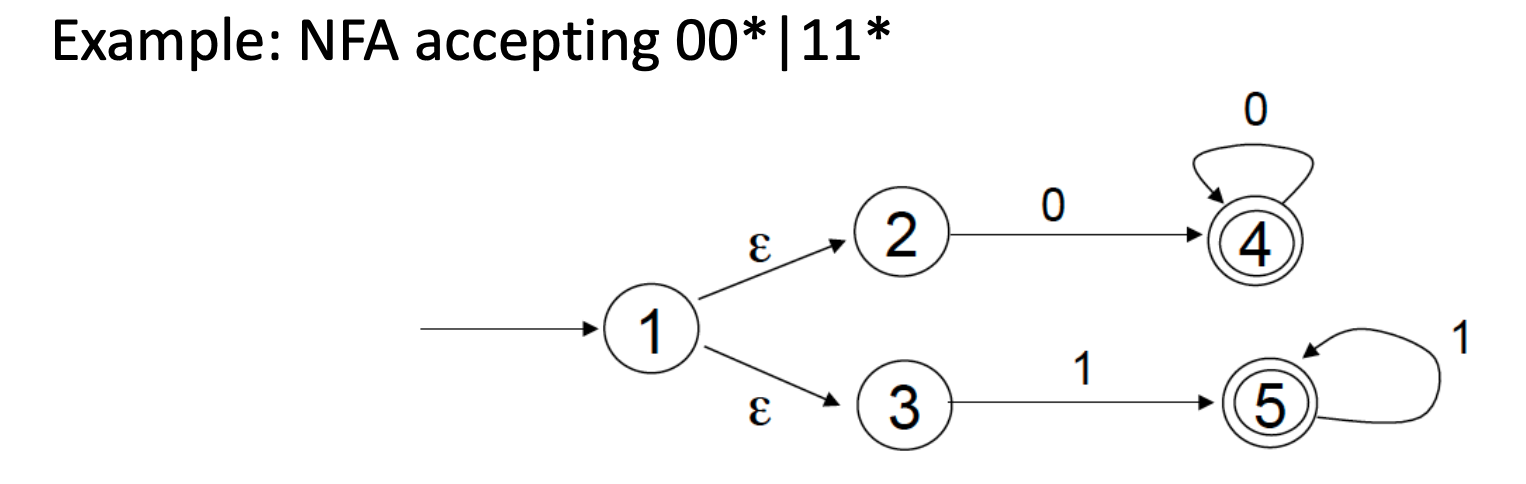
基于 NFA 的识别(决策)难以实施
- 在一个给定的状态下,可以从一个输入有多个转换
- Can have 𝜀-transitions
- 易于从正则表达式中形成
- 难以实现识别(决策)算法
另一种有限自动机:Deterministic Finite Automata (DFA)「确定性有限自动机 (DFA)」
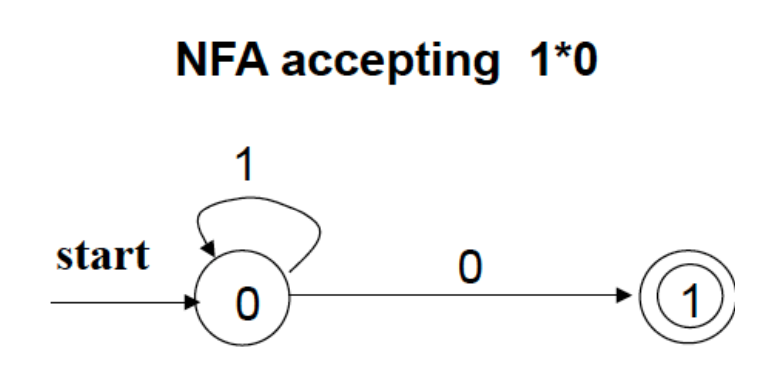
Regular Expression to NFA
每个正则表达式都可以转换为 NFA,遵循以下基本规则:
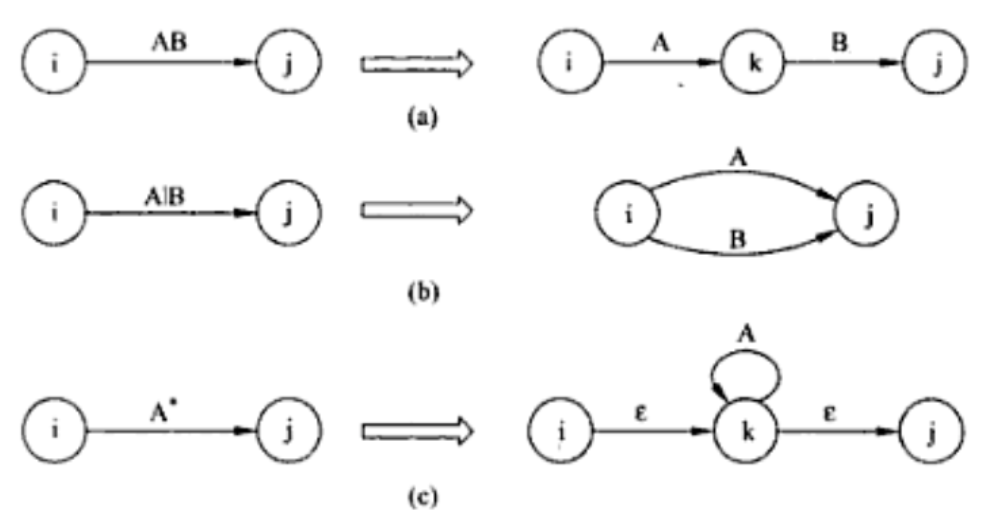
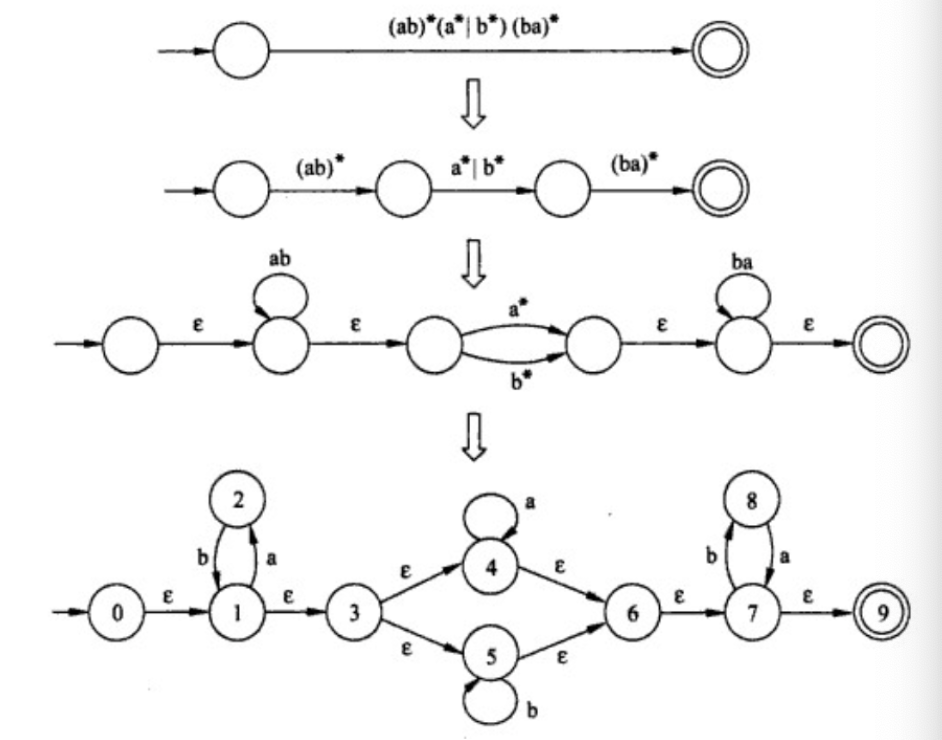
Example: regular expression to NFA
提示
- 拆开连接
- 逐步拆开外层表示
- 最后表示内层
确定性有限自动机(DFA)
Deterministic Finite Automata
每个状态下每个输入有一个过渡。
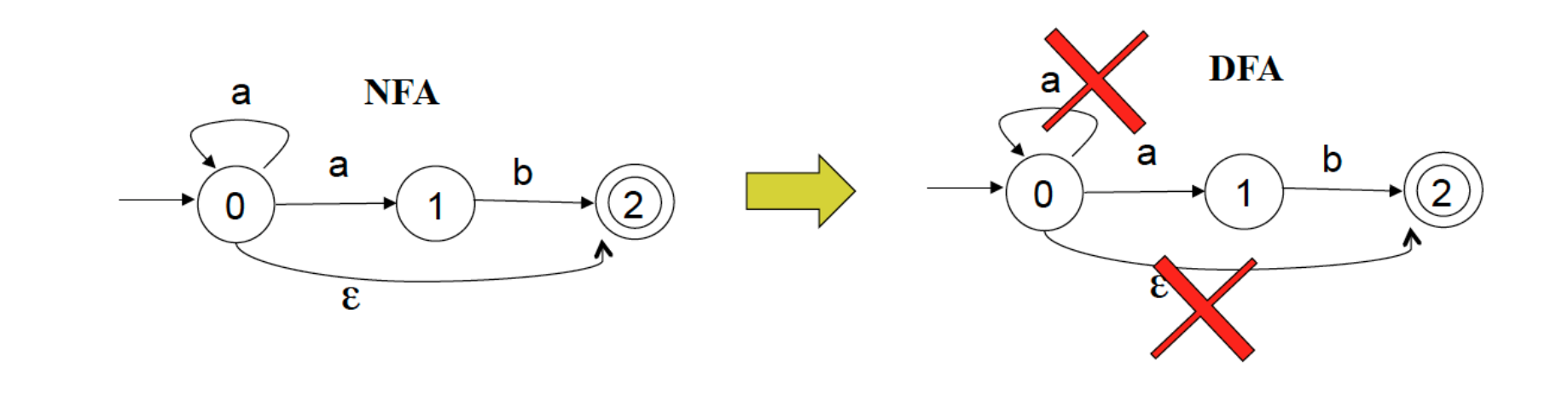
DFA 是 NFA 的一个特例:
- One transition per input per state
- No 𝜀-transitions
- NFA: 容易生成字符串。
- DFA: 易于生成和识别字符串。
- NFA:给定一个输入符号,可以进入几个状态中的任何一个。
- DFA:给定一个输入符号,只能进入一个确定性的状态。
- NFA:由于 𝜀 - 转换,当没有输入时可能会进入另一个状态。
- DFA:没有输入时哪里都不去;没有任何𝜀 - 过渡。
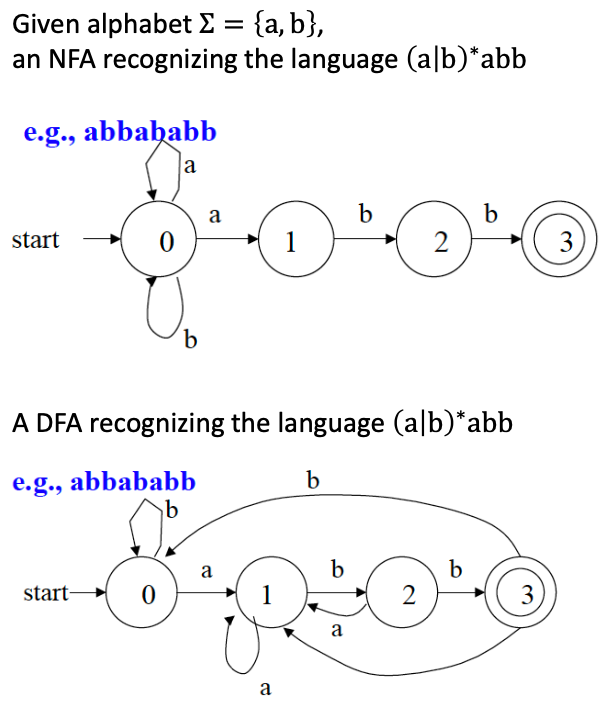
Table Implementation
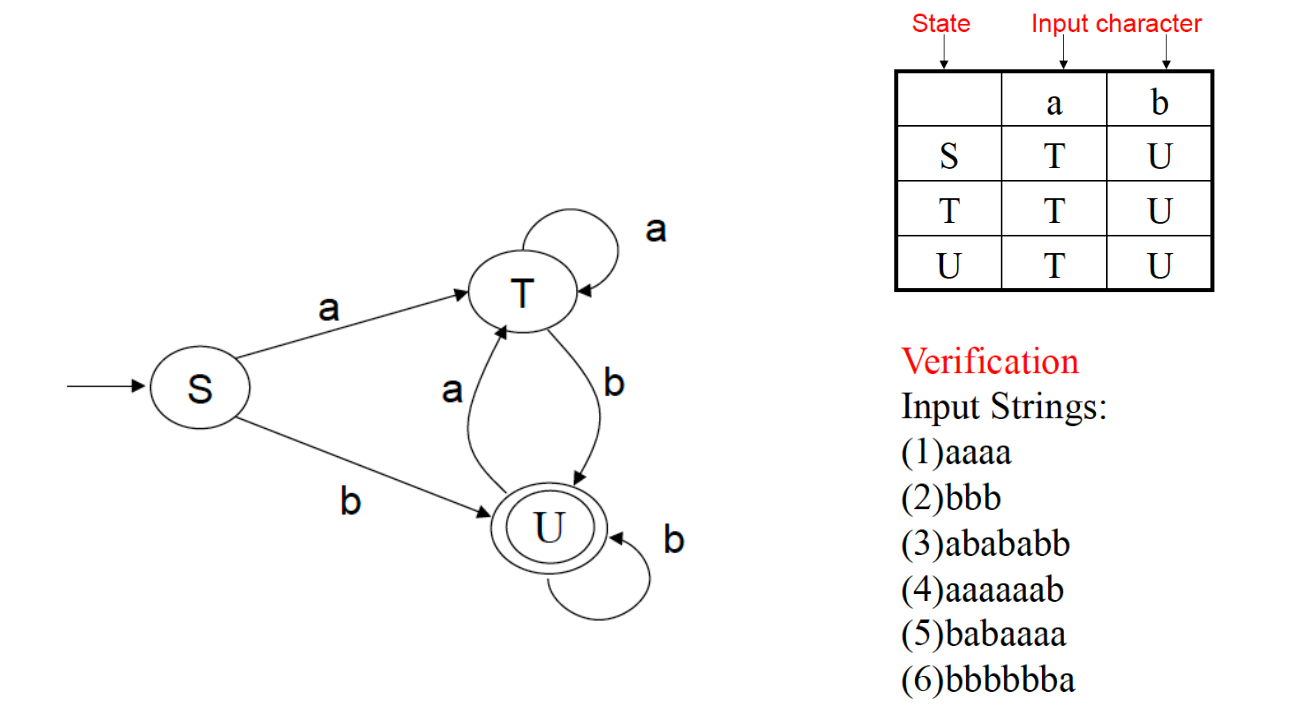
Algorithm: Simulating a DFA
- 输入:输入字符串𝑥,以文件末尾的字符eof为终点。
- DFA 𝐷,开始状态为𝑠0,接受状态集为𝐹。
- The answer “yes” if 𝐷 accepts 𝑥, “no” otherwise.
- Method:将以下算法应用于输入字符串𝑥。
- move(𝑠, 𝑐) 给出了从状态𝑠过渡到输入𝑐的状态。
- nextchar 返回输入字符串𝑥的下一个字符。