Regular Expressions

• The rules for specifying token patterns are called regular expression.「用于指定标记模式的规则被称为正则表达式。」
• A regular set (regular language) is the set of strings generated by a regular expression over an alphabet.「正则集（正则语言）是 由一个字母表上的正则表达式生成的字符串集。」

Alphabet and Strings

一个字母表「alphabet」（通常表示为Σ）是一个有限的符号集「finite set of symbols」。

• E.g. {0,1} is the binary digits alphabet;
• E.g. {a, b, ... , z, A, B, ... , Z} is the English letters alphabet.

在一个字母表 Σ 上的字符串「string」 𝑠 是一个从该字母表中抽取的符号的有限序列。

• 01001 is the string over Σ_{bin_digits} = {0,1}
• wxyzabc is the string over Σ_{lower_case_letters} = a, b, ... , z
• 𝜀 denotes the empty string (without any symbol)

The length of a string 𝑠 is denoted as |𝑠|. E.g. |𝜀| = 0; |101| = 3; |abcdef| = 6.

相关信息

𝜀 需要显式的在集合中写出来，以表示它的存在。

Kleene Closure and Language

字母表 Σ 的 Kleene closure，表示为 Σ^*，是 字母表 Σ上所有字符串的集合，包括空字符串 𝜀。

• E.g. given alphabet Σ = {0,1}, then Σ^* = {𝜀, 0, 1, 00, 01, 10, 11, 000, 001, ... }

注意

集合的元素是不重复的。

在一个字母表 Σ 上的任何字符串集，即 Σ^* 的任何子集，被称为语言「Language」。

• E.g. the empty set ∅, {𝜀}, Σ, and Σ^* are all languages;
• {abc,Def,D,z} is a language over Σ_letters = {a,b, ... ,z,A,B, ... ,Z}

Operations on languages

Language 是一个集合，因此所有集合操作都可以应用于 Language。需要注意的是，操作出来的结果都是集合。

Particularly union「交集」, concatenation「并集」, Kleene closure, and positive closure「即不含 𝜀」.

1667927831142.png

提示

LM 是 这种连接，必须是L的元素在前，M的元素在后。

Operations on Languages: Precedence

Kleene closure ≻ concatenation ≻ union

Examples for operations on languages, Given 𝐿 = {a,b} and 𝑀 = {a,bb}

241b4e311a783.png

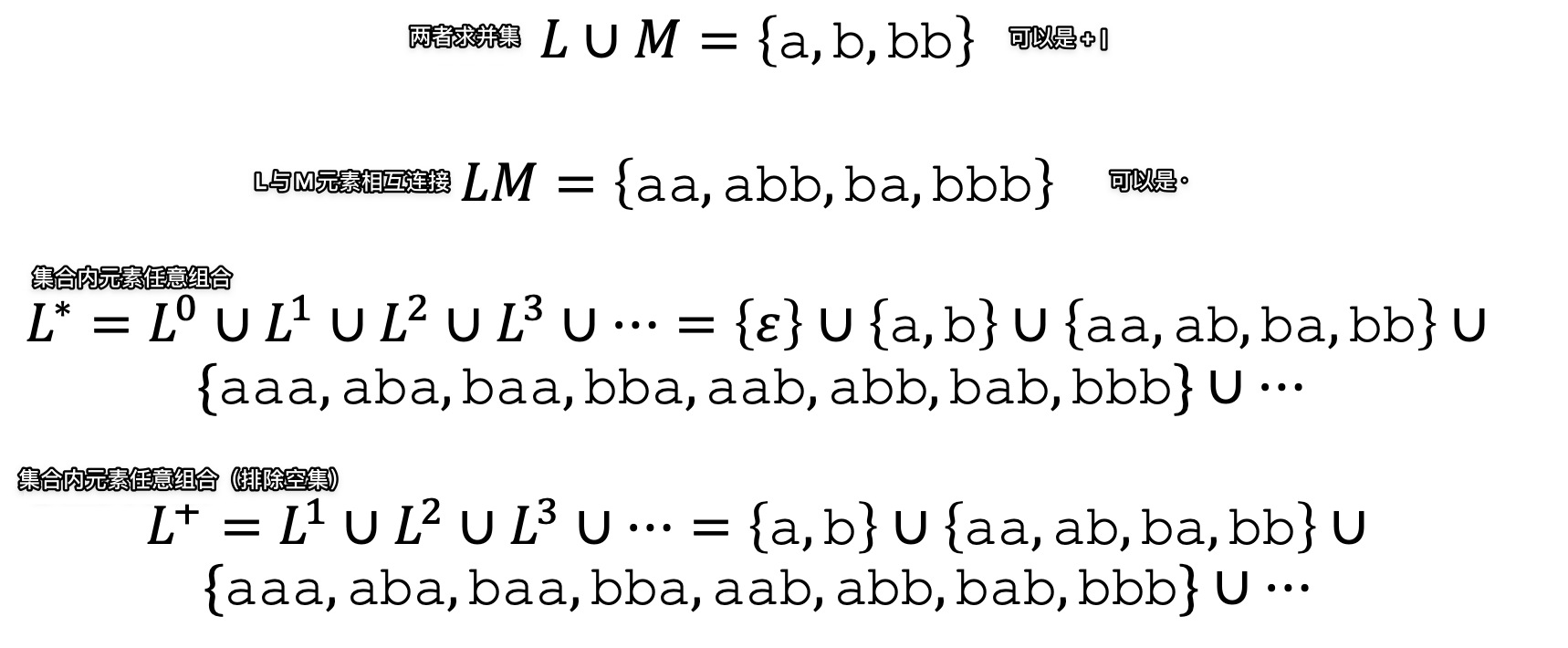
Another example for operations on languages,

正则表达式

在字母 Σ 上定义正则表达式的规则：

1. 空字符串 𝜀 是一个正则表达式，表示语言 {𝜀}
2. 单个符号 𝑎 ∈ Σ 是表示语言 {𝑎} 的正则表达式
3. 假设 𝑟 和 𝑠 是表示语言 𝐿（𝑟）和 𝐿（𝑠）的正则表达式，那么
   • (𝑟) | (𝑠) 是一个正则表达式，表示 𝐿 (𝑟) ∪ 𝐿 (𝑠)
   • (𝑟) | (𝑠）是一个正则表达式，表示 𝐿 (𝑟）𝐿(𝑠)
   • (𝑟)^* is a regular expression denoting (𝐿(𝑟))^*
   • (𝑟) is a regular expression denoting (𝐿 (𝑟) )

Regular Set (Regular Language): 每个正则表达式 𝑟 都表示一种**语言（集合）**𝐿 (𝑟) ，这被称为正则集（又称正则语言）。

E.g., given Σ = {a, b}, then a|b denotes the regular set {a, b}.

Example: Identifier in Pascal
Pascal identifier: a string of letters and digits beginning with a letter.

Regular definition:
LETTER → A|B| ... |Z|a|b ...|z
DIGIT → 0|1...|9
ID → LETTER(LETTER | DIGIT)∗

Example: Unsigned Numbers in Pascal
Unsigned numbers in Pascal are strings such as 5230, 39.37, 6.336E4, or 1.89E-4.

Regular definition:
OPTIONAL_FRAC → .DIGITS|𝜀
OPTIONAL_EXP → (E(+|−|𝜀)DIGITS)|𝜀
NUM → DIGITS OPTIONAL_FRAC OPTIONAL_EXP

提示

1. 单个字母表示 从集合中抽取1个元素
2. 可以从老虎机的角度理解 DIGITS OPTIONAL_FRAC OPTIONAL_EXP,就像有三个竖着的码表，转到谁是谁。

符号速记法

1. One or more instances: $r^{+} \stackrel{\text { def }}{=} r r^{*}$
2. Zero or one instance: $r ? \stackrel{\text { def }}{=} r \mid \varepsilon$
3. Character classes: $[a-z] \stackrel{\text { def }}{=} a|b| c|\ldots| z,[0-9] \stackrel{\text { def }}{=} 0|1| \ldots \mid 9$

1667963826783.png