Searching Algorithms

Goal

Given an array A of n numbers (in ascending order)

• Find the position of a key k from the array A
• return –1 if not found

A: | 1 | 3 | 8 | 12 | 17 | 23 | 35

Algorithm 1: Linear search

Assume k appears at most once in the array. Once k is found, the algorithm stops.

• Best Case: K is in the first element
• Worse Case: K is in the last element; element not found
• Average case: Half of the array is searched

for(int i=0;i<n;i++){
  if(A[i]==target){
    returni;
  }
else{
  return-1;
}

• Worse Case: O(n): K is in the last element/element not found
• Best Case: O(1): K is in the first element
• Average case: O(n): Half of the array is searched
• Overall, the running time of linear search is O(n): Most of the time we are interested in the worse case: You know for certain that the algorithm must perform at least that well「总体而言，线性搜索的运行时间为O（n）：在大多数情况下，我们对最坏的情况感兴趣：您可以肯定地知道该算法至少必须表现得很好」

Algorithm 2: Binary search

• Suppose someone picks a number k between 1 and 100
• You are allowed to ask questions of the form “Is k greater than x”, where x is an integer you choose
• Ask as few questions as possible

Binary search for a sorted array

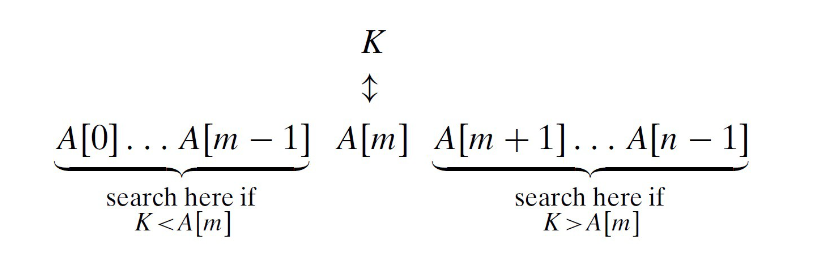
• Comparing a search key K with the array’s middle element A[m]「将搜索键K与数组的中间元素A [m]进行比较」
  • If they match, the algorithm stops;「如果它们匹配，则算法停止」
  • Otherwise, the same operation is repeated for the first half of the array if K <A[m] , or for the second half if K>A[m]
• When to stop: If the remaining array to be searched is empty, then the key cannot be found and return -1「如果要搜索的其余数组为空，则找不到键并返回-1」

Code

#include <iostream>
using namespace std;

int main() {
    //init the array and target value
    int arr[10] = {5,98,62,90,90,76,90,12,7,5};
    int target = 12;

    // sort the array
    const int ARRAY_SIZE = 10;
    int* data = arr;
    int insert;

    for (int next = 1; next < ARRAY_SIZE; next++) {
        insert = data[next];
        int moveItem = next;

        while ((moveItem > 0) && (data[moveItem - 1] > insert)) {
            data[moveItem] = data[moveItem - 1];
            moveItem--;
        }

        data[moveItem] = insert;
    }

    // show the sorted array
    for(int i = 0;i<10;i++){
        cout << data[i] << " ";
    }

    // search
    int l = 0,r= ARRAY_SIZE,m;
    while (l <= r){
        m = (l+r)/2;
        if(target == data[m]){
            cout << endl << m;
            break;
        } else if(target < data[m]){
            r = m - 1;
        } else{
            l = m + 1;
        }
    }

    return 0;
}

Example

Time complexity of binary search

• Basic operation: The number of times the search key is compared with an element of the array「搜索键与数组元素进行比较的次数」
• Assume three-way comparison: after one comparison of K with A[m], the algorithm can determine whether K is smaller, equal to, or larger than A[m]「在将K与A [m]进行一次比较之后，该算法可以确定K是小于，等于还是大于A [m]」
• Worse case: The key is not in the array「密钥不在数组中」

引用

• COMP1011 @ PolyU's PowerPoint