递归实践
大约 14 分钟
递归实践
递归分为单向递归和双向递归,我们日常说的递归是双向递归。
Introduction
递归的定义
编程语言中,函数 Func(Type a,……)直接或间接调用函数本身,则该函数称为「递归函数」。
在实现递归函数之前,有两件重要的事情需要弄清楚:
- 递推关系:一个问题的结果与其子问题的结果之间的关系。
- 基本情况(base case):不需要进一步的递归调用就可以直接计算答案的情况。可理解为递归跳出条件。
一旦我们计算出以上两个元素,再想要实现一个递归函数,就只需要根据递推关系调用函数本身,直到其抵达基本情况。
实际上,递归就是数学归纳法。
递归函数的特点
Example

- 有两种case:base case 和 general case
- general case 一般的情况
- base case:第一次到终点
- general case 的 return 需要调用自己,base return 不需要调用自己
一言以蔽之:我调用我自己
图解
一下图解为双向递归;
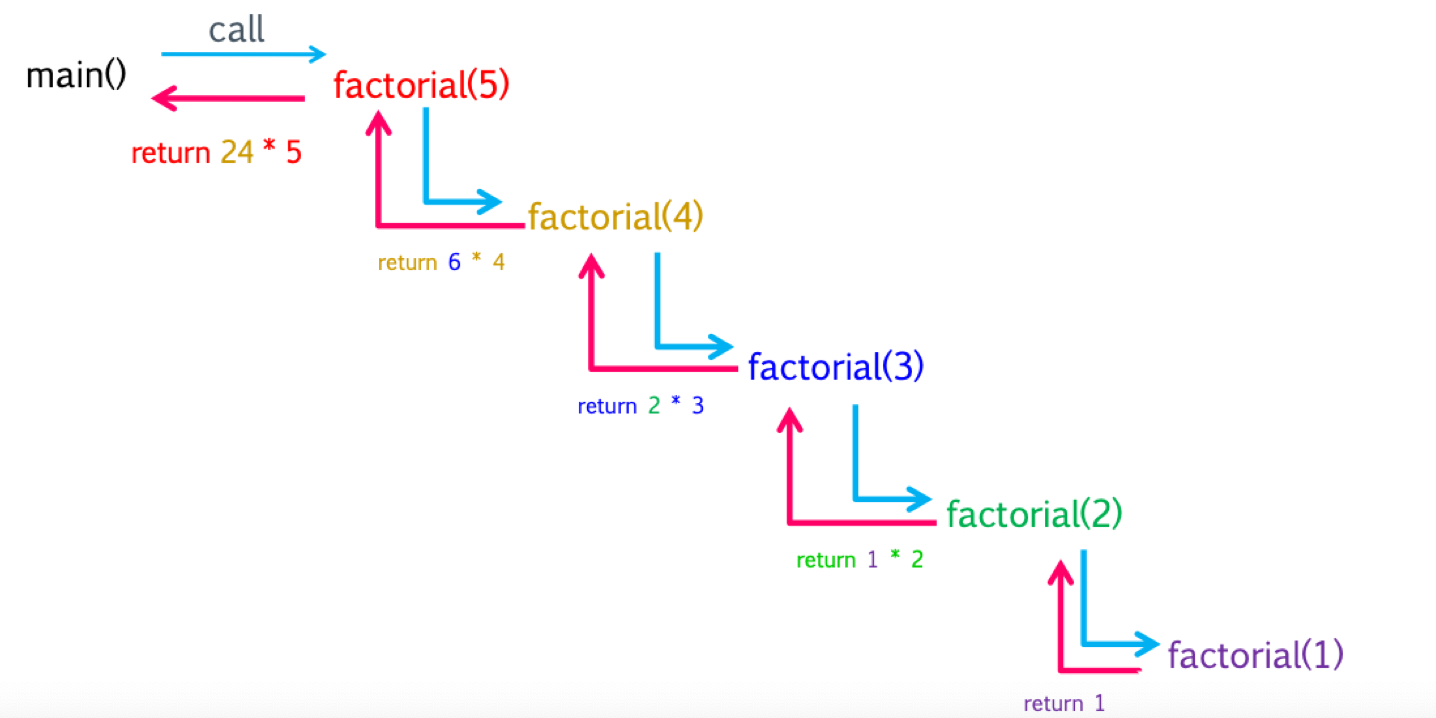
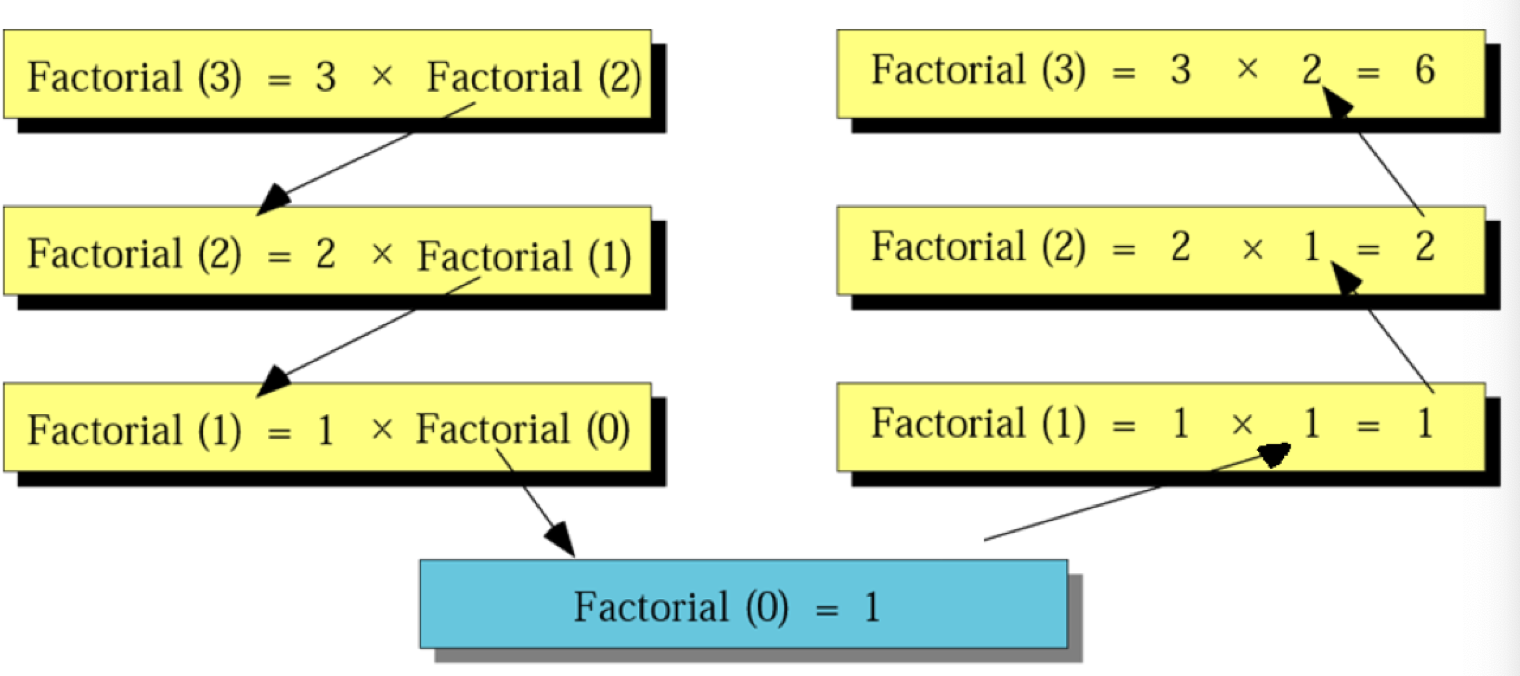
如何写出一个递归函数
范式:由下到上
- 寻找递归递推关系
- 寻找递归基本情况,跳出时返回基本情况的结果
- 修改递归函数的参数
- 递归调用并返回中间变量
- 使用递归函数的返回值与当前参数进行计算,并返回最终结果
实例: 累加——下面我们以累加的示例说明写递归的思路
1+2+3+4+...+n ,函数表达式为 f(n) = f(n-1) + n
寻找基本情况
累加示例中,基本情况为 n = 1 时,f(1) = 1。
寻找递推关系(难点)
累加示例中,递推关系为 f(n) = f(n-1) + n,f(n) 每次执行时依赖 f(n-1) 的结果,所以我们把 f(n-1) 的结果看作是中间变量。
中间变量其实就是联系递归函数的纽带,分析出中间变量递归函数也就实现了 80%。
大白话:当前结果必须借助前一个结果,前一个借助前前一个... 一直到时我们找到了「基本情况」。
然后拿到「基本情况」开始往回计算。这个过程我们简称为「由下到上」。
下面我们用 f(5) = 1 + 2 + 3 + 4 + 5 = 15 这个过程进行分析。
由下到上
在每个递归层次上,我们首先递归地调用自身,然后根据返回值进行计算。(依赖返回值)
/**
* 模拟程序执行过程:
* 5 + sum(4)
* 5 + (4 + sum(3)
* 5 + 4 + (3 + sum(2))
* 5 + 4 + 3 + (2 + sum(1))
* ------------------> 到达基本情况 sum(1) = 1 ,开始执行 ③ 行代码
* 5 + 4 + 3 + (2 + 1)
* 5 + 4 + (3 + 3)
* 5 + (4 + 6)
* (5 + 10)
* 15
* <p>
* 由下到上:最终从 1 + 2 + 3 + 4 + 5 计算...
* 递归函数「开始」部分调用自身,这个过程就是找到基本情况),然后根据返回值进行计算。
*/
实例: 帕斯卡三角
递推关系
下面的插图(来源力扣)给出了一个 5 行的帕斯卡三角,根据上面的定义,我们生成一个具有确定行数的帕斯卡三角形。
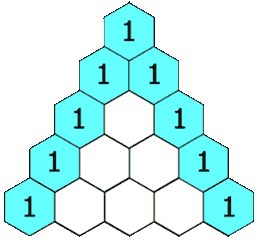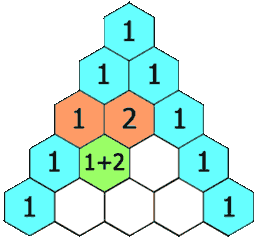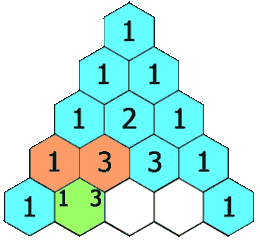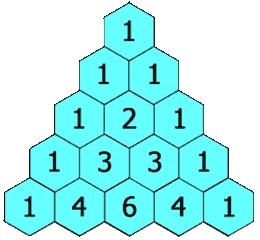
首先,我们定义一个函数 f(i, j),它将会返回帕斯卡三角形第 i 行、第 jj列的数字。可以看到,每行的最左边和最右边的数字是基本情况,它总是等于 1。
每个数是它左上方和右上方的数的和。
- 递推关系:f(i, j) = f(i - 1, j - 1) + f(i - 1, j)
- 基本情况:f(i,j) = 1 ,当 j=1,j=1 或者 i=j 时。
单向递归和双向递归
单向递归
单向递归又叫做由上到下的递归。
特点
- 多个传递变量
- 传递变量的个数 = 形参个数
- 形参中包括一个中间变量,用于存放最终结果
- base case 用于返回最终结果
举例
#include <iostream>
using namespace std;
int asum(intnumber,intoutcome){
//base
if (number==0){
return outcome;
}
//general
outcome *= number;
number -= 1;
return asum(number,outcome);
}
int main(){
cout << asum(3,1);
return 0;
}
范式
由下到上-范式
- 寻找递归递推关系
- 寻找递归基本情况,跳出时返回基本情况的结果
- 修改递归函数的参数
- 递归调用并返回中间变量
- 使用递归函数的返回值与当前参数进行计算,并返回最终结果
通用代码
int fun(参数,中间变量) {
// base case
if (基本情况条件){
return 基本情况的结果与中间变量的计算结果;
}
// general case
中间变量 = 根据参数与中间变量重新计算;
修改参数;
return fun(参数,中间变量);
}
双向递归
特点
- 通常只有一个形参
- 中间变量不需要传递
- base case 返回 最基本情况的结果
- general case 返回 最终结果
举例
#include <iostream>
using namespace std;
int asum(int number){
// base
if (number == 0){
return 1;
}
// general
int outcome = asum(number-1);
outcome *= number;
return outcome;
}
int main() {
cout << asum(3);
return 0;
}
通用代码
int fun(参数) {
// base case
if (基本情况条件){
return 基本情况的结果; }
// general case
变量1 = fun(修改后的参数);
最终结果 = 根据 修改前的参数 与 变量1 计算;
return 最终结果;
}
引用
- https://leetcode-cn.com/circle/article/koSrVI/
- COMP1011’s PowerPoint