跳至主要內容

Advanced Topics

Hirsun大约 55 分钟

Advanced Topics

Web Architecture

  • 互联网是一个由计算机网络组成的世界性网络
  • 网络是互联网最受欢迎的服务之一，提供对数十亿网页和动态内容的访问。-> 实现众多的数据处理和商业交易活动
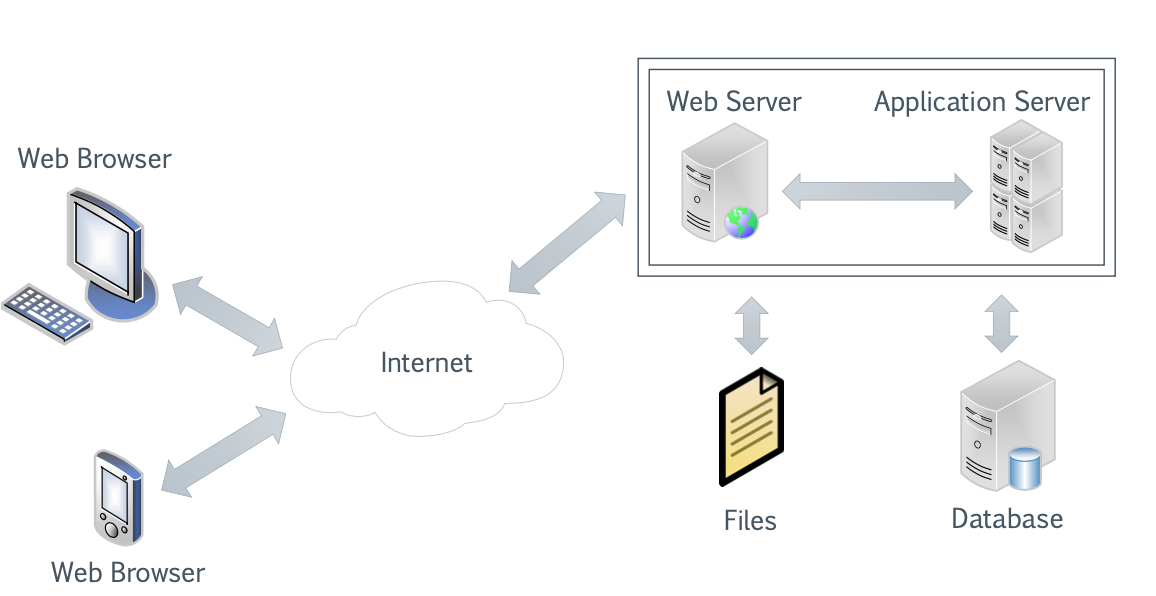
1682386781596.png
1682386781596.png
  • Hypertext transfer protocol (HTTP)
  • An application layer protocol (Layer 7 in OSI model)
  • Client/Server model
  • Stateless: 服务器不保留任何关于过去客户请求的信息

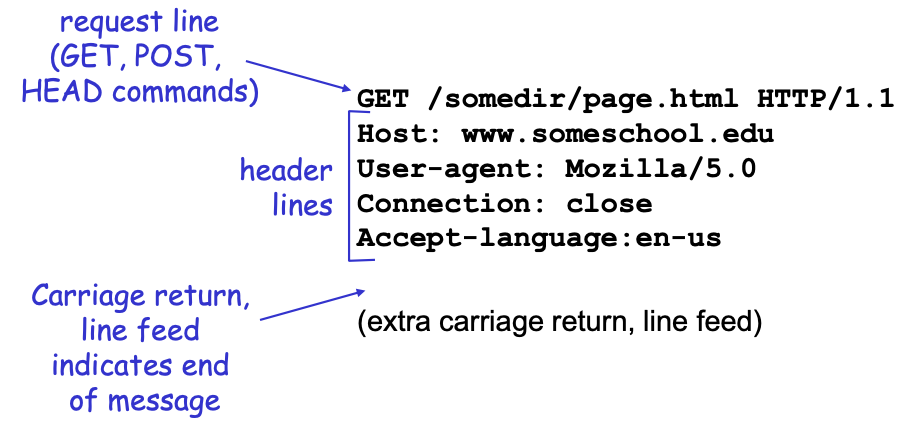
HTTP Request Message

1682387073088.png
1682387073088.png
1682387086481.png
1682387086481.png

Top Website Vulnerabilities

  • Cross-sitbe scripting (XSS): 坏网站向无辜的受害者发送脚本，从一个诚实的网站上窃取信息
  • Cross-site request forgery (CSRF): 坏网站向好网站发送浏览器请求，使用无辜受害者的凭证

Cross-Site Request Forgery (CSRF)

  • 跨站请求伪造（CSRF）是一种攻击，它迫使终端用户在他们目前已被验证的网络应用程序上执行不需要的行动。
  • CSRF攻击专门针对改变状态的请求，而不是窃取数据，因为攻击者没有办法看到对伪造请求的响应。
    • 在社会工程的帮助下（如通过电子邮件或聊天发送链接），攻击者可以欺骗网络应用程序的用户执行攻击者选择的行动。
  • 如果受害者是一个正常的用户，一个成功的CSRF攻击可以迫使用户执行改变状态的请求，如转移资金，改变他们的电子邮件地址，等等。
  • 如果受害者是一个管理账户，CSRF可以损害整个网络应用。

Countermeasures

  1. 使用安全的Cookie属性：设置 Cookie 的“Secure”属性，以确保它只在HTTPS连接中传输。还可以设置“SameSite”属性，以限制第三方网站发送请求时的Cookie传输。
  2. 使用双重提交 Cookie：在这种方法中，你将在Cookie和请求头中发送相同的 CSRF 令牌。当服务器接收到请求时，它会比较这两个值。如果它们匹配，则请求被视为合法。
  3. 在请求中包含一个随机生成的、不可预测的CSRF令牌：这种方法更加安全，因为攻击者无法预测或猜测这个令牌。将这个令牌包含在请求中，并在服务器端验证它是否与服务器存储的令牌匹配。服务器将新生成的 Token 返回给用户，并将其放在 HTML 正文中。
  4. 对请求使用Referer和Origin头检查：通过检查Referer和Origin头，你可以确保请求来自合法的来源。然而，这种方法并不是100%可靠，因为某些浏览器和网络配置可能不发送这些头信息或者这些浏览器会伪造这些消息，或者攻击者可能伪造它们。
  5. 添加验证码
  6. 使用受信任的浏览器

Non-persistent XSS

  • 恶意代码由受害者的浏览器执行，有效载荷「Payload」不存储在任何地方；相反，它作为服务器发送的响应 HTML 的一部分被返回。
  • 因此，受害者被骗向有漏洞的网络应用程序发送恶意代码，然后被反射到受害者的浏览器，在那里执行XSS有效载荷
  • 非持久性XSS也被称为1型XSS，因为攻击是通过单一的请求/响应周期进行的。
反射型跨站脚本攻击（Reflected XSS）

反射型跨站脚本攻击（Reflected XSS）是一种常见的 Web 安全漏洞，攻击者通过发送包含恶意脚本代码的 URL 链接来实施攻击。当受害者点击这个链接时，Web 应用程序将在响应中包含这些恶意脚本，从而导致浏览器执行这些脚本。攻击者通常会利用这些脚本来窃取用户数据，如 cookie 和登录凭据等。

反射型 XSS 之所以会被执行，原因如下：

  1. 不充分的输入验证：很多 Web 应用程序没有充分地验证用户输入，这使得攻击者可以在 URL 参数中插入恶意脚本。当服务器接收到这个包含恶意脚本的请求时，它可能将这些脚本嵌入到响应的 HTML 中，从而导致浏览器执行这些脚本。
  2. 不充分的输出编码：当 Web 应用程序将用户输入嵌入到 HTML 响应中时，如果没有进行适当的输出编码，恶意脚本就有可能被浏览器解释为有效的脚本代码并执行。正确的输出编码可以将潜在的脚本代码转换为不可执行的文本，从而避免 XSS 攻击。
  3. 浏览器执行脚本：浏览器默认会执行 HTML 中的脚本代码。因此，当恶意脚本成功地被嵌入到响应的 HTML 中时，浏览器会自动执行这些脚本。攻击者通常会利用这一特性来实施反射型 XSS 攻击。

URL 通常是 GET request，为什么会在浏览器中被执行？

实际上，URL 本身并不会被执行。然而，在反射型 XSS 攻击中，恶意脚本是通过 URL 参数传递给服务器的。当 Web 应用程序接收到这些带有恶意脚本的参数时，它可能会将这些参数插入到响应的 HTML 页面中。这就是恶意脚本在浏览器中被执行的原因。

以下是一个简单的例子来说明这个过程：

  1. 攻击者创建了一个包含恶意脚本的 URL，例如：https://example.com/search?query=<script>alert('XSS')</script>
  2. 受害者点击这个 URL 链接，浏览器向服务器发起一个 GET 请求，其中包含恶意脚本作为参数。
  3. Web 应用程序接收到这个请求，并将参数（包括恶意脚本）插入到响应的 HTML 页面中，例如：<div>搜索结果：<script>alert('XSS')</script></div>
  4. 浏览器接收到响应，并按照正常流程解析 HTML。当浏览器遇到恶意脚本时，它会将其视为有效的 JavaScript 代码并执行。

因此，关键在于 Web 应用程序在处理 GET 请求参数时没有进行足够的验证和编码。要防止反射型 XSS 攻击，开发者需要对输入数据进行验证和编码，并在可能的情况下，使用内容安全策略 (CSP) 限制可执行的脚本来源。

Persistent XSS

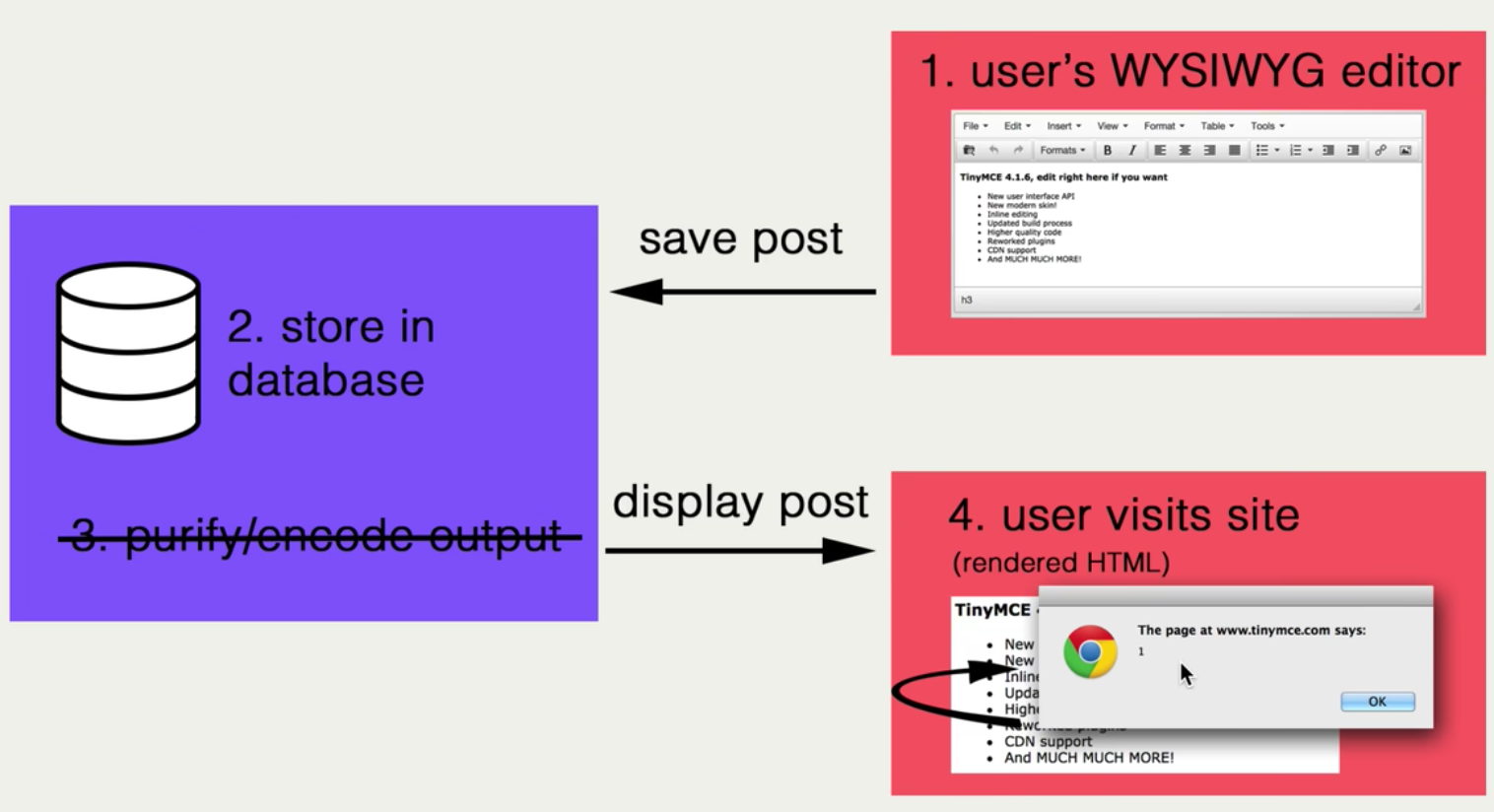
1682404623456.png
1682404623456.png
  • 有效载荷被保存在一个二级存储（数据库）中
  • 持久性攻击造成的损害可能比非持久性攻击更严重。
  • 警如发帖中发出包含恶意代码的内容，其它用户访问到该内容后，满足特定条件即触发。

如何阻止 XSS 攻击？

  1. 输入验证：对所有用户输入进行严格的验证，确保输入数据符合预期的格式和规范。尽量避免接受和处理未经验证的数据。使用白名单验证策略，只允许通过已知安全的数据。
  2. 输出编码：在将用户输入插入到 HTML 页面中时，务必进行适当的输出编码。针对不同的上下文（如 HTML、属性值、JavaScript 等），使用相应的编码方法。例如，将 < 替换为 <、 > 替换为 > 等。
  3. 使用 HTTP-only Cookie：将敏感信息（如会话 ID）存储在 HTTP-only 的 Cookie 中，以防止恶意脚本通过 JavaScript 访问这些信息。HTTP-only Cookie 只能通过 HTTP 请求发送，无法通过客户端脚本访问。
  4. 实施内容安全策略（CSP）：CSP 是一种安全策略，可以限制浏览器加载和执行的脚本来源。通过配置 CSP，可以仅允许从可信来源加载和执行脚本，从而降低 XSS 攻击的风险。例如，通过设置以下 CSP 头部，可以仅允许从当前域名加载脚本：Content-Security-Policy: script-src 'self'
  5. 使用安全编程库和框架：许多现代 Web 开发框架和库（如 React、Angular、Vue.js 等）已经内置了防止 XSS 攻击的安全措施。确保正确使用这些框架和库，并始终保持它们的版本更新。
  6. 使用受信任的浏览器

总结就是

  1. 对输入（和URL参数）进行过滤
  2. 对输出进行编码
  3. Cookie 设置 http-only

Protect Web Communication

保护网络客户和服务器之间的通信

两种主要方法

  • 在应用层面实施安全功能
  • 更灵活，更多的控制 - 可能有更严格的安全性
    • 例如，S/MIME和PGP
  • 在运输或网络层面实施安全功能
    • 上层应用的共同服务
    • 减轻应用开发的负担
      • E.g., SSL/TLS and IPSec

Transport Layer Security

传输层安全（TLS）握手协议负责建立安全会话所需的认证和密钥交换。

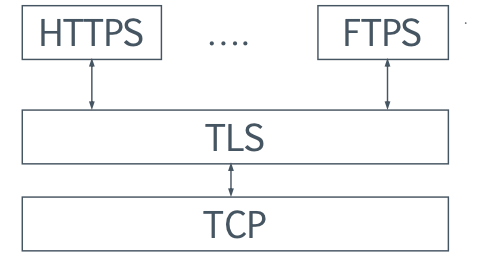
1682389735116.png
  • SSL（安全套接字层）是由网景公司在1994年提出的。
  • 后来，互联网工程任务组（IETF）成立了一个工作组，对安全套接字层（SSL）进行标准化。
  • 由此产生的协议，称为传输层安全（TLS），几乎与 SSL 3.0 相同
  • 现在建议客户和服务器都使用TLS 1.1或以上版本
  • 主要用于网络（http）流量，但也可用于其他应用协议（例如，ftp、telnet等）。
  • 当建立一个安全会话时，握手协议管理以下内容
    • 密码套件的协商
    • 对服务器和可选的客户端进行认证
    • 会话密钥信息交换

提示

默认情况下，SSL现在在Internet Explorer中被禁用。现在所说的 SSL 其实都是 TLS。

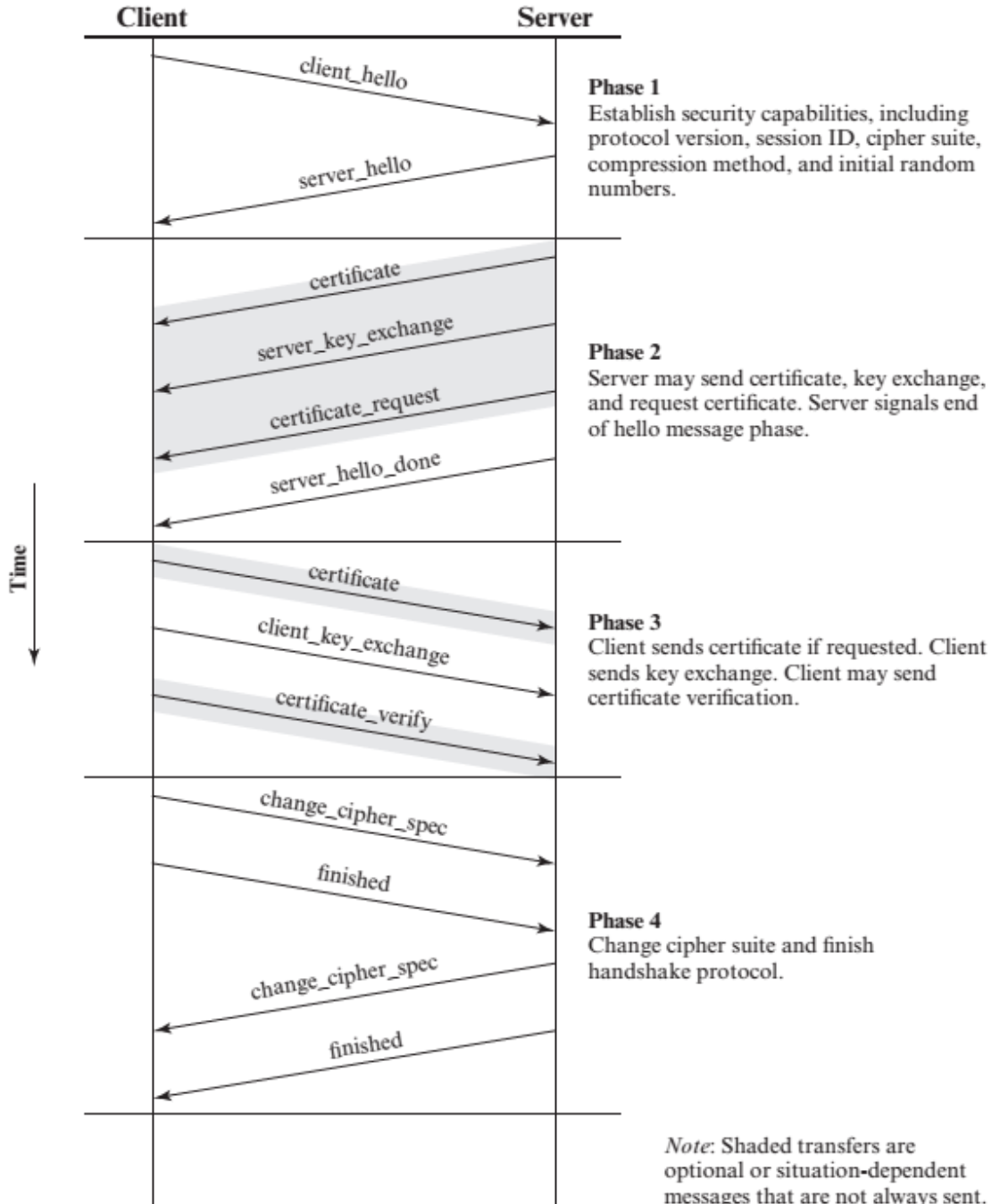
Handshake

  1. 客户端向服务器发送一个 "Client hello "消息，以及客户端的随机值和支持的密码套件（例如，TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384）。
  2. 服务器通过向客户端发送 "Server hello "消息进行响应，同时发送服务器的随机值
  3. 服务器向客户端发送其证书以进行认证，并可要求客户端提供证书。服务器发送 "Server hello done "消息。
  4. 如果服务器向客户要求提供证书，客户就会发送该证书。
  5. 客户端随机生成一个 Pre-Master Secret 并用服务器证书中的公钥对其进行加密，将加密后的 Pre-Master Secret 发送给服务器
  6. 服务器收到 Pre-Master Secret。服务器和客户端各自根据Pre-Master Secret生成Master Secret。会话密钥由Master Secret依次生成
  7. 客户端向服务器发送 "Change cipher spec "通知，表明客户端将开始使用新的会话密钥进行散列和加密信息。客户端还发送 "客户端完成 "消息
  8. 服务器收到 "Change cipher spec "并将其记录层安全状态切换为使用会话密钥的对称加密。服务器向客户端发送 "服务器完成 "消息
  9. 客户端和服务器现在可以通过他们建立的安全通道交换应用数据。从客户端到服务器以及从服务器到客户端发送的所有信息都使用会话密钥进行加密。
1682390824115.png
1682390824115.png
TLS 能不能防止重放攻击?

传输层安全（TLS）协议在一定程度上可以防止重放攻击，但并非绝对安全。TLS 提供了一定程度的保护，主要是通过以下几个方面来防止重放攻击：

  1. 握手协议：在 TLS 握手过程中，客户端和服务器之间会交换随机数（Client Random 和 Server Random），并用这些随机数来生成会话密钥。由于每次握手时随机数都是不同的，因此攻击者无法轻易地重放握手过程。
  2. 序列号：在 TLS 会话期间，双方会为每个消息分配一个递增的序列号。如果接收方收到具有相同序列号的两个消息，它将检测到这是一个重放攻击并拒绝处理这些消息。
  3. 消息完整性检查：TLS 使用消息验证码（MAC）来确保消息的完整性。由于攻击者不知道会话密钥，因此很难篡改消息并使其通过完整性检查。

TLS 在很大程度上可以抵抗重放攻击，但并非完全防御。要确保更高的安全性，可以使用其他安全措施，如时间戳、一次性令牌或多因素认证等。

Example

TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA384

  • ECDHE：椭圆曲线Diffie-Hellman Ephemeral（ECDHE）是一种密钥交换算法，用于在客户端和服务器之间安全地建立共享密钥。与传统的Diffie-Hellman（DH）相比，ECDHE使用椭圆曲线密码学，提供了相同安全级别下更短的密钥和更高的计算效率。Ephemeral表示临时的，意味着每次连接都会生成新的密钥对，从而提供前向保密（FS）。
  • ECDSA：Elliptic Curve Digital Signature Algorithm（ECDSA）是一种基于椭圆曲线密码学的数字签名算法。在此密码套件中，服务器使用ECDSA对其证书签名以及在握手过程中的关键消息进行签名，从而确保身份验证和数据完整性。
  • AES_256_CBC：Advanced Encryption Standard（AES）是一种对称加密算法，这里使用的是256位密钥长度。CBC表示密码块链（Cipher Block Chaining）模式，它是一种加密模式，用于将AES应用于整个数据块序列。
  • SHA384：Secure Hash Algorithm（SHA）是一种密码哈希算法，SHA384表示输出哈希值长度为384位。在此密码套件中，SHA384用于生成消息认证码（MAC），以确保数据在传输过程中的完整性。

ECDH用于生成安全的共享密钥，而AES用于加密和解密实际的通信数据。

在TLS通信中，以下是如何将这些组件配合使用的：

  1. 客户端和服务器使用ECDHE进行密钥交换，从而建立共享密钥。此过程保证了通信的保密性。
  2. 服务器使用ECDSA签名算法对其证书和关键消息进行签名，从而确保身份验证和数据完整性。
  3. 使用共享密钥，客户端和服务器之间的数据使用AES_256_CBC进行加密和解密。
  4. 使用SHA384生成消息认证码（MAC），确保数据在传输过程中的完整性。

通过这种方式，TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA384密码套件将TLS和ECDH（一种DH变种）结合起来，实现了一种安全、可靠的加密通信方案。

Ring Signature

我作为一个选民，不希望别人知道我在电子投票系统中的投票情况，因为在这个系统中投票是公开的。

创建一个环形签名：

  • 您为您的投票创建一个环签名，其中包括所有选民或（部分人口）的公钥
  • 公众只能知道投票是由公钥的所有者之一投出的，但不知道具体是谁。

以一个投票场景为例

  • 其中有三位投票者：Alice、Bob 和 Carol。
  • 他们分别有自己的公钥和私钥对 (PA, SA), (PB, SB), (PC, SC)。

假设 Alice 想要投票，但不希望别人知道她的投票结果。因此，她决定使用 Ring Signature 保护自己的隐私。

在生成环签名时，我们采用以下步骤：

  1. Alice 计算哈希值 k = h(m)。
  2. 选择一个随机初始化值 v。
  3. 为环中其他成员（Bob 和 Carol）选择随机值 x1 和 x2。然后，计算 y1 = gB(x1) 和 y2 = gC(x2)。
  • 注明：函数 g 是一个加密函数，拥有公钥可以正向计算，又有私钥可以反向计算。
  1. 有 v
  • 计算 a = Ek(v XOR y1)
  • 计算 b = Ek(a XOR y2)
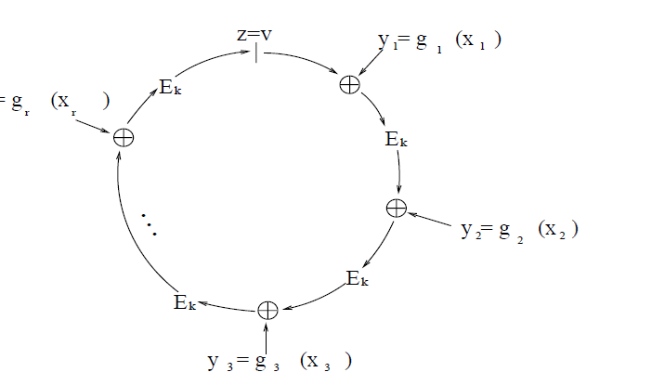
  • 像环一样，并入所有的成员后
    • 可以推导出 ys = Ek(Ek(v XOR y1) XOR y2)
    • 计算 xs = gA^(-1)(ys)。
  1. 环签名将是：(PA, PB, PC; v, x1, x2, xs)。

验证时，

1682649577458.png

为什么环签名能够隐藏身份？

  1. 隐私性：环签名的核心特性是隐私性，它通过将实际签名者的密钥与一组其他潜在签名者的密钥混合在一起，形成一个环。环内的所有成员都具有相同的权重，因此无法确定哪个成员实际创建了签名。
  2. 非对称加密：环签名使用非对称加密，即每个用户都有一对密钥，一个公钥和一个私钥。公钥用于验证签名，而私钥用于生成签名。由于只有签名者知道其私钥，因此其他人无法伪造签名。
  3. 数学原理：环签名的设计基于复杂数学原理，如离散对数问题和椭圆曲线密码学。这些原理确保了在不知道实际签名者私钥的情况下，无法通过计算来分辨签名者身份。

Zero-Knowledge Proof

在不透露证人的情况下，让人相信某项陈述是在语言中的。

一个具体的例子，为了让你知道 "我是公钥的所有者"，而不给你我的私钥。

  • 如果你知道我的私钥，你就能够验证我是所有者。然而，你永远知道我的私钥!
  • 那么，如果有一种方法可以在不透露我的私钥的情况下说服你？

=> Zero-Knowledge Proof (ZKP) (of knowledge)

假设 Alice 拥有一对密钥 (y, x) 使得 y = g x mod p

  • 给定 y 是公开的，Alice如何使Bob相信Alice是这个密钥对的所有者（因为Alice用x来生成y）？
    • 不直接把 x 给 Bob
    • Alice 是证明者，Bob 是验证者
  • 这是一个实际的例子，说明如何验证一个人的公钥。
    • 所有者必须证明他/她知道 x！

给出 (y,g,p)，x 的值是多少，使 y = g x mod p ?

  • Step 1
    • 爱丽丝从{0, ..., p - 1} 中随机挑选 r
    • Compute T = g r mod p
    • Send T to Bob
  • Step 2
    • Bob picks a random challenge, c, from
    • Send c to Alice
  • Step 3
    • If c = 0, prover sets z = r
    • If c = 1, prover sets z = r + (x mod p) -1
    • Alice 将 z 发送给验证者
  • Step 4
    • Verifier checks if gz = T yc mod p
      • if c = 0, verifier receives r
      • if c = 1, verifier receives r+x
    • 重复这个过程很多次!

概括地说

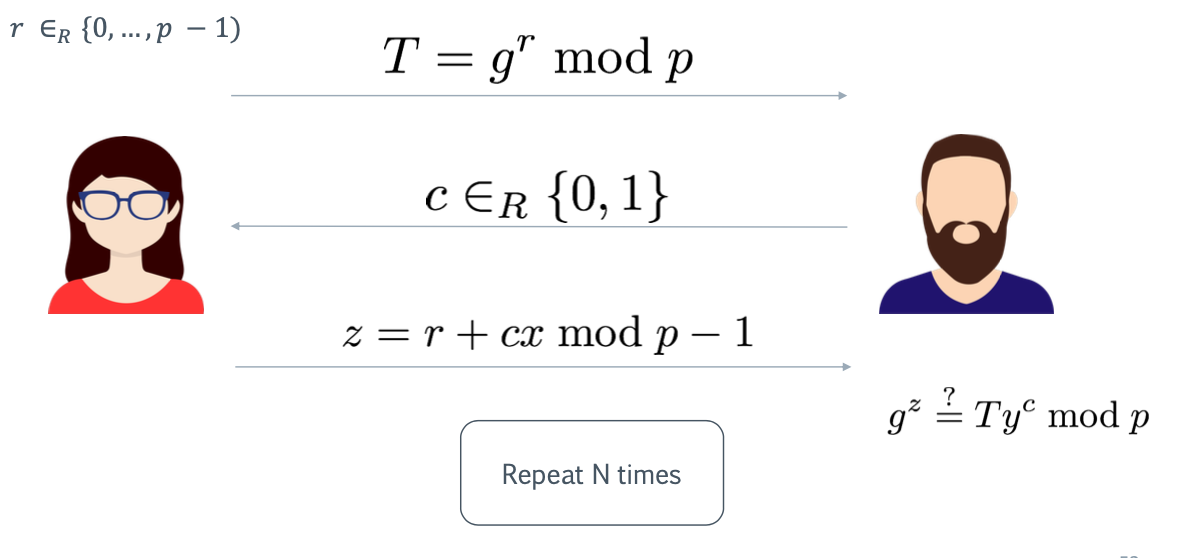
1682651350476.png
1682651350476.png

为什么这个协议有效？

  • 完整性：如果 Alice 知道 x，她总能正确回答
  • 健全性：如果爱丽丝总是能够回答挑战，那么她很可能既知道 r 又知道 x +(r mod p) -1 -> 这意味着她知道 x
  • Zero-knowledgeness
    • 验证者只学习 r 或 x + (r mod p) - 1
    • 没有透露任何关于 X 的信息

为什么要重复很多次？

Bob 可以通过多次重复这个过程来增加对 Alice 知道私钥 x 的信心。在每次迭代中，Alice 都有 50% 的机会在不知道私钥 x 的情况下成功通过挑战。

因此，通过多次迭代，Alice 在不知道私钥 x 的情况下欺骗 Bob 的概率会降低。同时，这个过程不会泄露关于私钥 x 的任何信息。

过程梳理

在这个场景中，有两个参与者：证明者（Alice）和验证者（Bob）。Alice 希望向 Bob 证明她知道私钥 x，而不直接泄露 x 的值。为此，我们使用了上述的零知识证明协议。

证明者（Alice）知道：

  1. 私钥 x。
  2. 公钥 y。
  3. 公共参数 g 和 p。
  4. 随机数 r，这是 Alice 在协议开始时选择的。
  5. 挑战值 c，这是 Bob 发给 Alice 的。
  6. 响应值 z，根据挑战值 c 计算得出。

验证者（Bob）知道：

  1. 公钥 y。
  2. 公共参数 g 和 p。
  3. Alice 发给他的临时值 T。
  4. 挑战值 c，这是 Bob 随机选择的。
  5. Alice 发给他的响应值 z。

验证者（Bob）不知道：

  1. 私钥 x，这是 Alice 想要保密的关键信息。
  2. 随机数 r，这是 Alice 在协议开始时选择的。

在零知识证明中，我们需要证明协议的完整性、健全性和零知识性。现在，让我们通过数学计算来推理为什么这个协议是可行的。

完整性：如果 Alice 知道私钥 x，则她总是能正确回答 Bob 的挑战。

当 c = 0 时，Alice 返回 z = r，那么 g^z = g^r = T，这与 Alice 发送给 Bob 的 T 相匹配。

当 c = 1 时，Alice 返回 z = r + (x mod p) - 1，那么 g^z = g^(r+(x mod p)-1) = g^r * g^((x mod p)-1) = T * g^((x mod p)-1)。我们知道 y = g^x mod p，所以 y * g^(-1) = g^((x mod p)-1)。因此，g^z = T * y * g^(-1)。

这表明，如果 Alice 知道私钥 x，她总是能正确回答挑战。

健全性：如果 Alice 总是能正确回答挑战，那么她很可能知道私钥 x。

由于 Alice 能正确回答挑战，她必须知道 r 和 r + (x mod p) - 1。因此，她可以计算出 (r + (x mod p) - 1) - r = x mod p - 1。这意味着 Alice 知道私钥 x。

零知识性：验证者只学习 r 或 x + (r mod p) - 1，而不会透露任何关于 x 的信息。

我们已经在完整性部分证明了 g^z = T * y^c mod p 这个等式成立，而且 z 的值取决于随机挑选的 r 和挑战 c。在协议中，c 和 r 都是随机选取的。因此，验证者（Bob）无法从 z 中提取任何关于私钥 x 的信息。这保证了零知识性。

综上所述，这个零知识证明协议是可行的，因为它满足了完整性、健全性和零知识性。

Legends never die.
Copyright © 2024 Hirsun