Basic Cryptography III

Hirsun大约 30 分钟

Basic Cryptography III

Symmetric Key Management

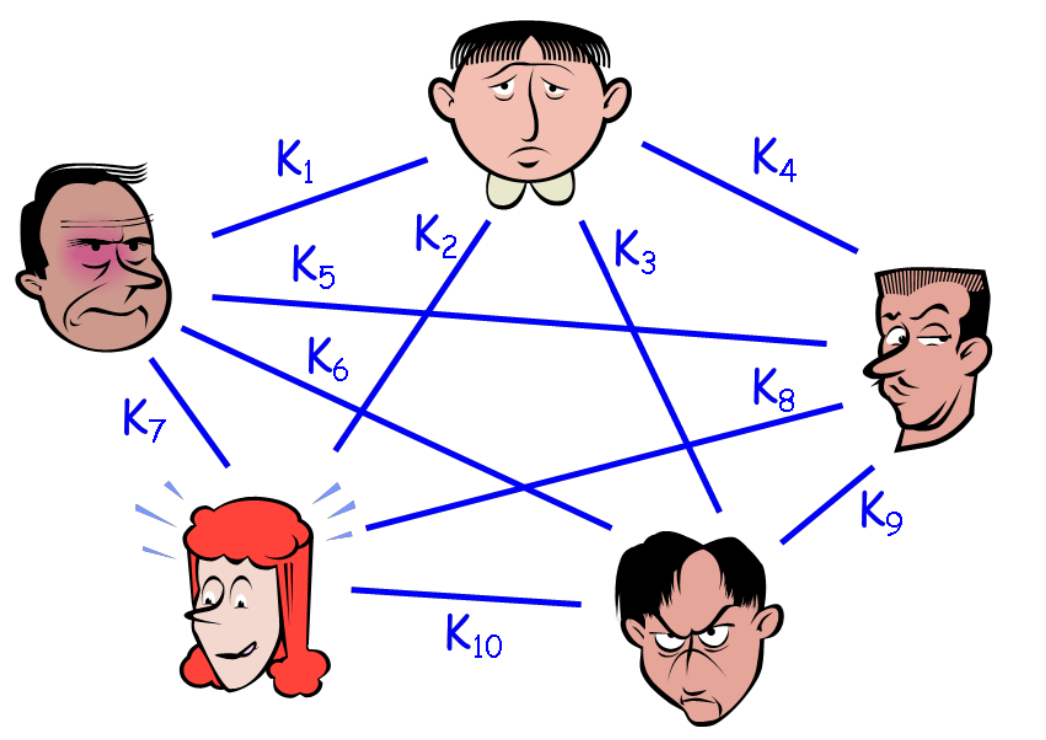
每一对通信实体都需要一个共享密钥
对于一个 n 方系统，系统中有 n(n-1)/2 个不同的密钥，每一方需要维护n-1 个不同的密钥。
如何减少系统中共享钥匙的数量？
- 集中式密钥管理「Centralized key management」
- Public keys

Centralized Key Management

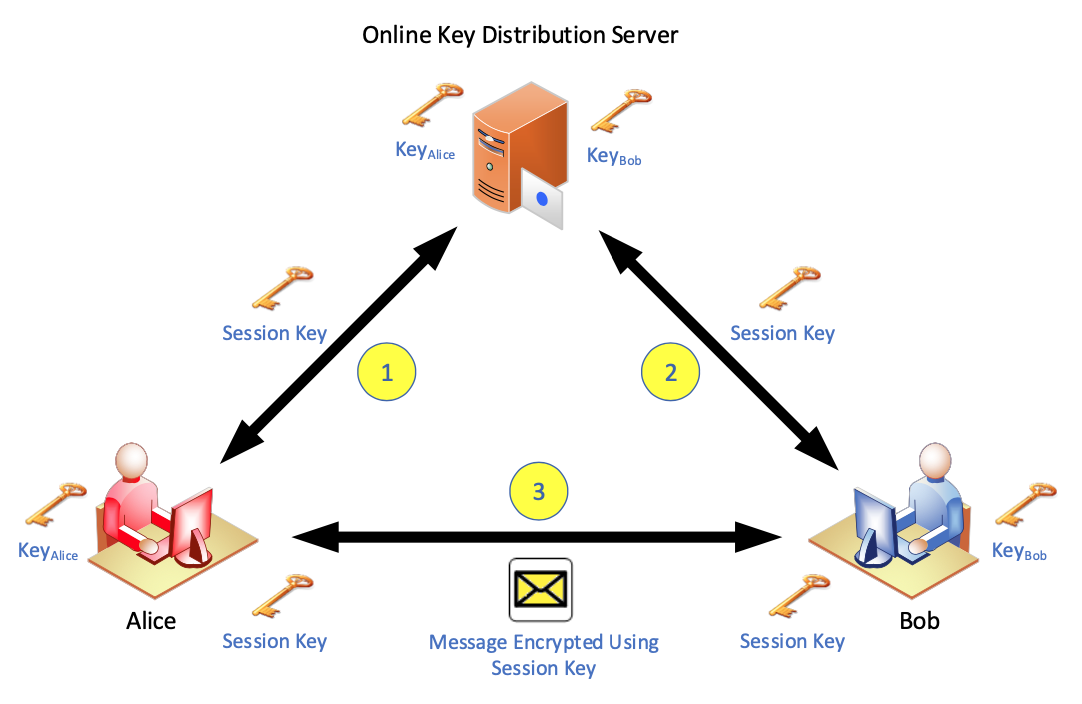
只有n个长期密钥「ong-term secret keys」，而不是系统中的 n(n - 1)/2
每个用户与服务器共享一个长期秘钥
Secret keys are used only for the secure delivery of session keys
Real data are encrypted under session keys

Public Key Encryption

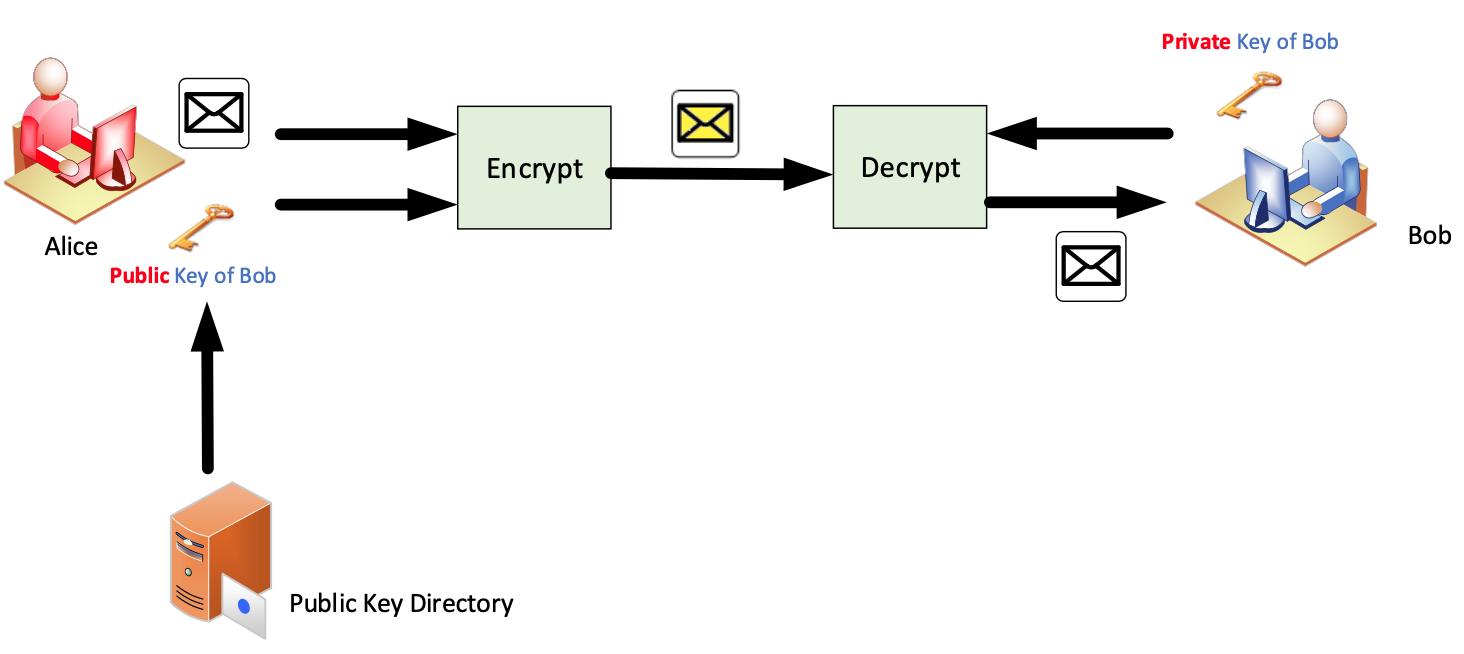
接收者Bob有一个密钥对：公钥和私钥
- 发布公钥，使密钥为公众所知
- Bob 将私钥保密
其他人使用 Bob 的公钥为 Bob 加密消息
Bob 使用他的私钥解密

安全要求：

难以从密文中找到私钥或明文
很难从公钥中找到私钥

Motivation of Public Key Crypt

对称密钥算法的问题
- 发送方需要一个安全的方法来告诉接收方加密密钥的信息
- 您可能与之通信的每个人都需要一个单独的密钥（可扩展性问题）
公钥算法使用公钥和私钥对来解决这两个问题
- 每个接收器都有一个密钥对
- 公钥是公开的（已发布）
- 发送方使用接收方的公钥对信息进行加密
- 只有接收方可以用相应的私钥解密

RSA Encryption Algorithm

最著名和最广泛使用的公钥计划
安全性依赖于大数因式分解的难度
- (对于RSA）给定一个整数n，找出两个整数p和q，使n=pq
- Factorization is sub-exponential (hard)

RSA 原理

要使用 RSA 算法对数据进行加密和解密，首先要确定分组的大小。为了实现这一步，必须确保该分组可以保存的最大数值要小于n的位数。

随机选择两个大的、长度大致相等的质数，p 和 q, (p<q)
- E.g., |p| = |q| = 512 bits
设定 n = p * q（n 称为公共模数）
随机选择 e，使得 $\operatorname{gcd}(e, \varphi(n))=1$ $gcd (e, φ (n)) = 1$
- $\varphi(n)=\varphi(p q)=(p-1)(q-1)$
- $\operatorname{gcd}(e, \varphi(n))=1$ 指 e 与 (p - 1) * (q - 1) 互质
- e 被称为 公共指数「public exponent」
计算 d 使得 $de \bmod \varphi(n) = 1$ $d e mod φ (n) = 1$
- d is called the private exponent

modular inverse

If we said x is the modular inverse of 7 modulo 26, it means

7x \bmod 26 = 1

It could be written as

$7x ≡ 1 \ (mod \ 26)$
$7 \equiv x^{-1} \bmod 26$
$a × 7 + b × 26 = 1$

可以通过尝试使用 Euclidean algorithm 计算出来，也可以通过遍历算出来，因为 If a modular inverse exists, there will be exactly one solution between 0 and m-1, where m is the modulus (本案例为 26).

设定好数字后

Public Key「PK」 is (n, e)
Private Key 「SK」 is d

之后

Encryption: $c = M^e \bmod n$ $c = M^{e} mod n$
- M is plaintext
- c is ciphertext
Decryption: $M=C^{d} \bmod n$ $M = C^{d} mod n$
- Since $\left(M^{e}\right)^{d} \bmod n= M\operatorname{mod} n = M$

Note: The exponent, say x, is calculated by x mod $\varphi(n)$ . For simplicity, we just write x.

Example

Choose two primes p = 47 and q = 71
- n = pq = 3337
随机选择 e 使其与 $\varphi(n)$ $φ (n)$ 互质
- $\varphi(n)=(p-1)(q-1)=46 \times 70=3220$
- E.g., e = 79
Compute $d \equiv e^{-1} \bmod \varphi(n)$ $d \equiv e^{- 1} mod φ (n)$
- d = 79^-1 (mod 3220) = 1

Extended Euclidean

Assume $de \bmod \varphi(n) = 1$
let a = e, b = $\varphi(n)$ , a < b

ax + by = gcd(a, b)

We want x, since d = x
- x = x mod b, 0 < x < b, if x is exist
- y < 0

x = -193, y = 176
let x = x mod b = -193 + 999 = 806
Therefore, d = x = 806

Security

RSA算法的强度取决于对 大数进行质因数分解的难度，即很难通过 $\varphi(n)$ 得到 d。

已知公钥 <e, n>，如果密码分析者可以分解 n = pq，则得到 $\varphi(n)$ = (p - 1)(q - 1)
Knowing e and $\varphi(n)$ , d can be obtained easily

蛮力攻击可能吗？

RSA 公共指数 e 的值可以很小，例如 16 比特长，但 d 的值应该很大，例如至少 1000 比特长。

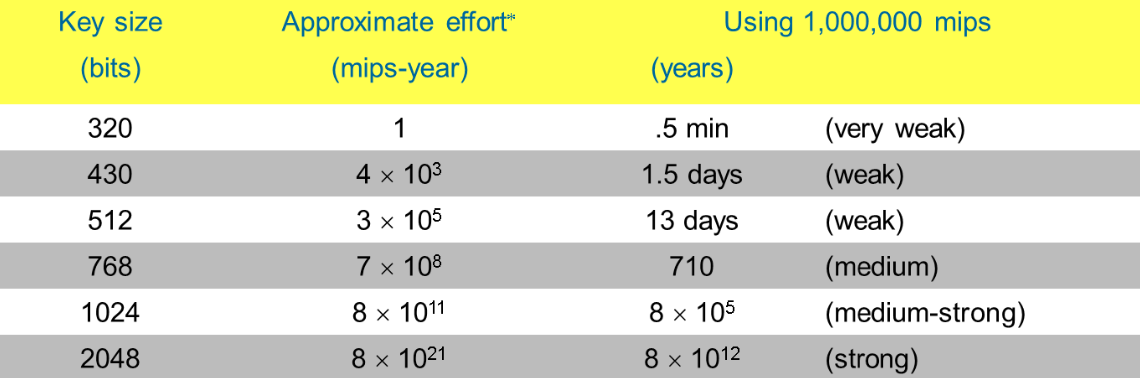
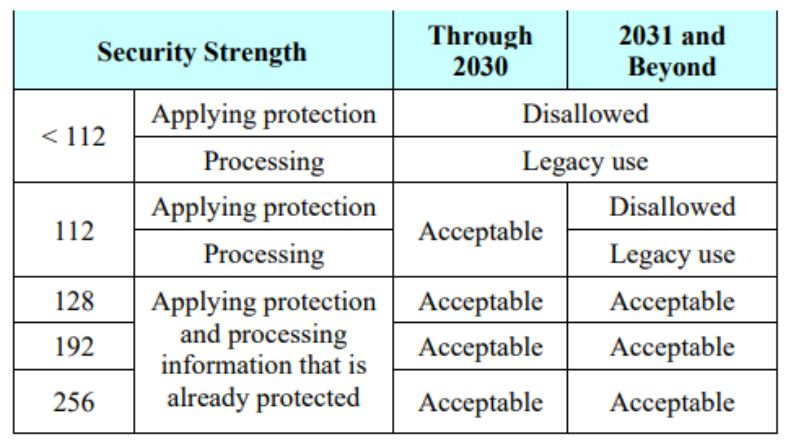
从以上实际试探来看，512位的RSA密钥，以前被认为足以满足一些商业应用的需求，现在却存疑了。对于高安全性要求，可以考虑使用 2048 位密钥

密钥大小的安排应考虑到数据的寿命，跨越未来几十年的时间。

Problem of Public-Key Crypt

公钥密码学（PKC）可用于保密或认证。
但公钥算法很慢（由于大量的指数化运算）。
所以通常我们使用对称密钥加密来保护信息内容，比如使用 " session key"，并使用 PKC 来加密会话密钥
- Merkle’s Secret Key Distribution
- Diffie-Hellman Key Exchange

Comparison

Symmetric key	Public key
Two parties MUST trust each other	Two parties DO NOT need to trust each other
Both share the same key	Two separate keys: a public and a private key
Attack approach: brute force	Attack approach: solving mathematical problems (e.g., factorization, discrete log problem)
Faster	Slower (100 - 1000 times slower)
Smaller key size	Larger key size
Examples: AES, DES, 3DES, ChaCha20...	Examples: RSA, ElGamal, ECC,...

Merkle’s Secret Key Distribution

梅克尔在1979年提出
A生成一个新的临时密钥对
A 向 B 发送公钥和 A 的身份信息
B 生成一个会话密钥 K，并使用A的公钥将其加密后发送给A。
A使用A的私钥恢复加密的内容
A和B使用K来保证后续通信的安全

Diffie–Hellman Exchange

DH 可以让双方在完全缺乏对方(私有)信息的前提条件下通过不安全的信道达成一个共享的密钥。此密钥用于对后续信息交换进行对称加密。

DH 方法针对的是以下困难的局面：Alice 和 Bob 想共有一个密钥，用于对称加密。但是他们之间的通信渠道是不安全的。所有经过此渠道的信息均会被敌对方：Eve看到。哪他们要如何交换信息，才能不让Eve知道这个密钥呢？

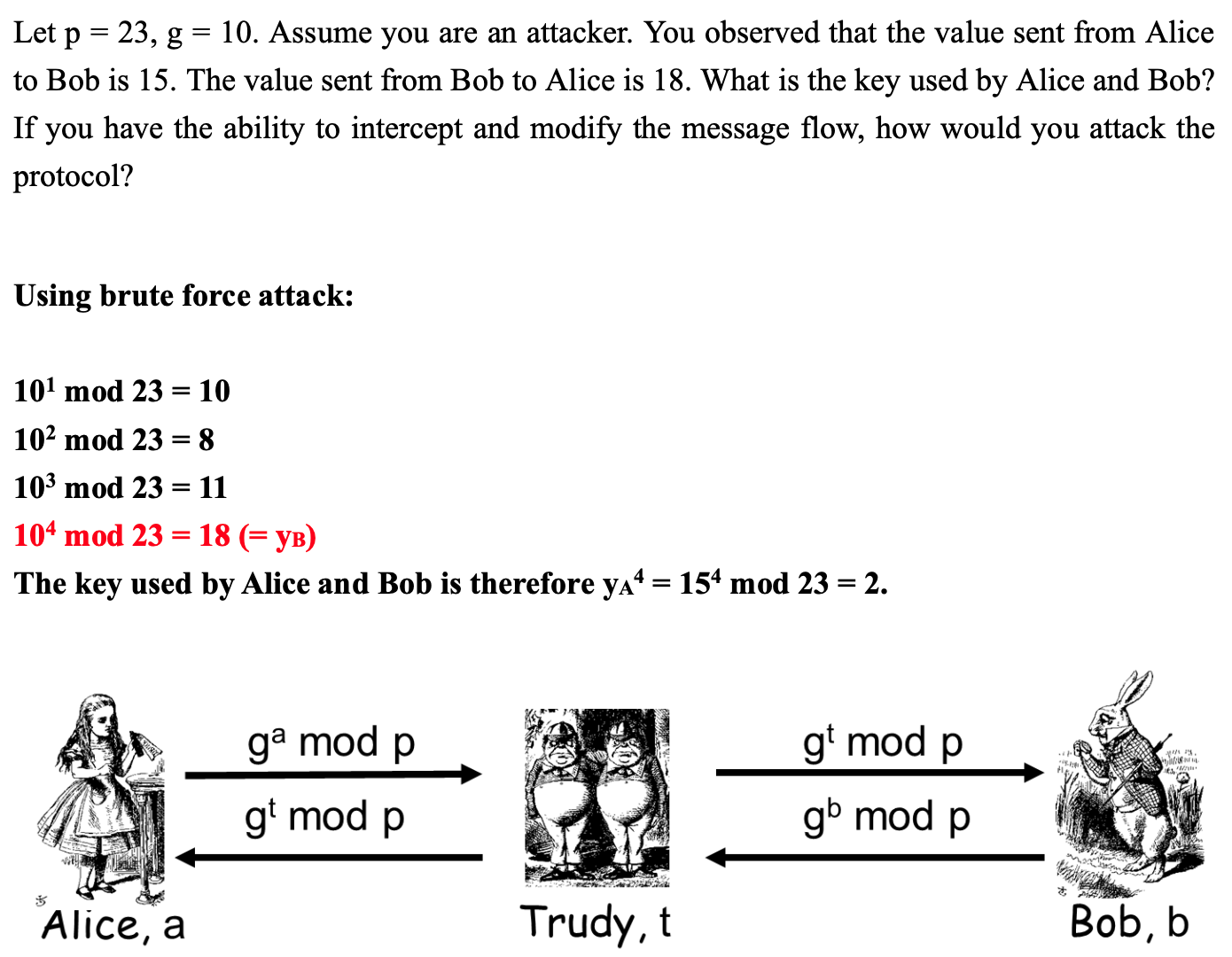
以下是DH协议的方案：

Alice 和 Bob 先对 g 和 p 达成一致，而且公开出来。Eve也就知道它们的值了。
Alice 取一个私密的整数 a，发给Bob 计算结果：A = g^a mod p.
Bob 取一私密的整数 b, 发给 Alice 计算结果 , B = g^b mod p.
Alice 计算出 S = B^a mod p = g^ab mod p
Bob 计算出 S = A^b mod p = g^ab mod p
Alice 和 Bob 现在就拥有了一个共用的密钥 S

虽然 Eve 看见了 g, p , A and B，但是鉴于计算离散对数的困难性，她无法知道 a和 b 的具体值。所以 Eve就无从知晓密钥 S 是什么了。

暴力破解

Digital Signatures

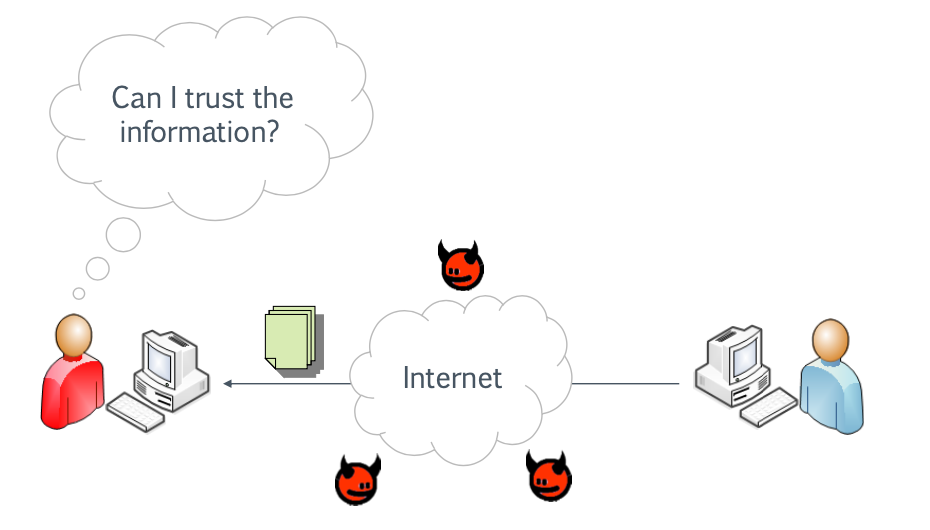
有一份电子文件要从 Alice 发给 Bob，是否与手写签名有功能上的等同性？

Alice 可以轻松地在文档上签名
但其他人很难伪造
Bob 或任何人都可以轻松验证

解决方案：数字签名

Sign using Alice’s private key
Verify using Alice’s public key

Basic Model

只有签名者（拥有私钥）才能在消息 m 上生成有效签名 σ
任何人（因为发布了相应的公钥）都可以验证关于 m 的 σ 是否有效

思考：如何将公钥与发布者联系起来，确认该公钥是由发布者发布的？发布者会不会因为躲避某些责任而不承认文档和公钥为发布者发布的呢？这回使得应用场景发生哪些局限？

RSA Signature Scheme

Setup
- n = pq where p, q are large prime (say 512 bits long each)
- ed mod (p-1)(q-1) = 1
- Signing (Private) Key : d
- Verification (Public) Key : (e, n)
Signature Generation: S = M^d mod n
- where M is the message to be signed
Signature Verification
- If S ^e mod n = M, output valid;
- otherwise, output invalid

HTTPS 方案设想

客户端协商一个加密函数（如chacha20）和加密密码。
客户端把协商好的函数和密码使用公钥加密，发给服务端。
服务端用私钥解密后，回复给客户端同意该加密方案。
客户端收到后通知后，就开始这样的来回的使用对称方案加密。

公钥公证可以找证书证书签发商验证，或者与自己电脑上的根证书做对比等。

注明：这只是我的早期猜想。

考虑 RSA 签名方案，如果 M > n，如何对 M 进行签名？

Choose a bigger n? Generally No
Divide M into smaller pieces such that M = m1||m2...||mn and sign them one-by-one? Generally No

Hash Signature Scheme

Alice 不是直接对 M 签名，而是对 M 的哈希签名，用 H(M) 表示。

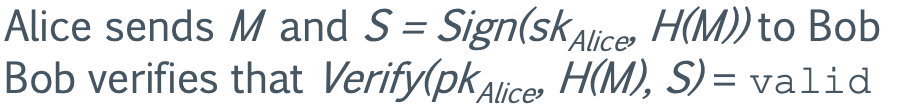
H is called a hash function
H 将任意长度的二进制字符串映射为小于 n 的非零整数
H(M) is called the message digest「信息摘要」

Hash Function

用公钥数字签名方案对信息摘要进行签名

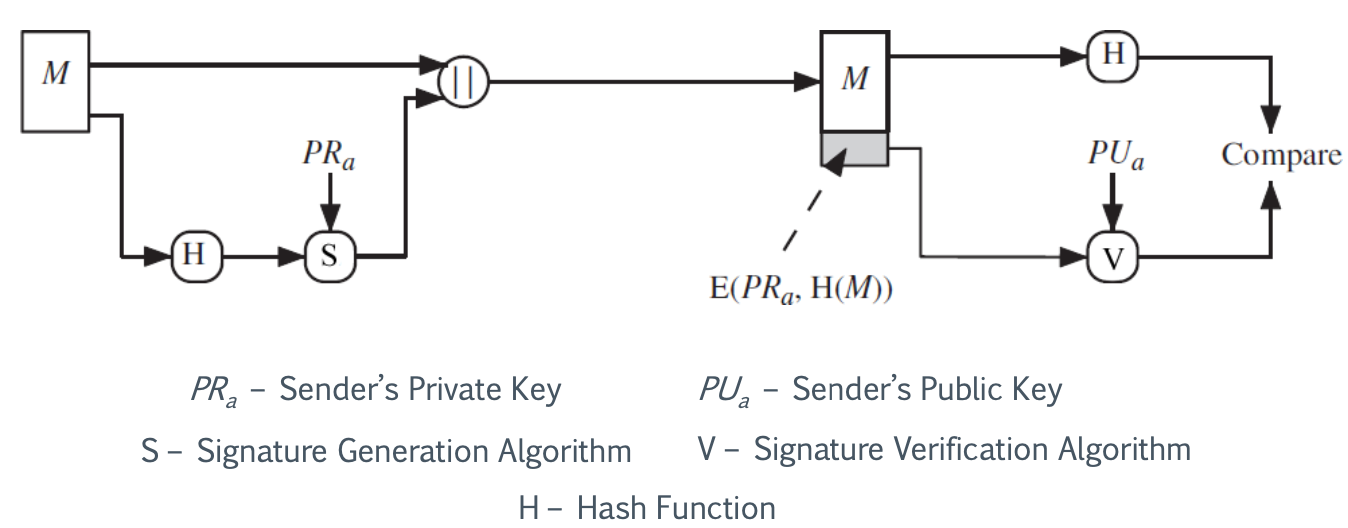
Well known hash functions: MD5, SHA-1, SHA-2
由于抗碰撞，不同的信息应该被散列成不同的信息摘要。

Requirements for Hash Functions

can be applied to any sized message M
produces fixed-length output h
is easy to compute h = H(M) for any message M
one-way property: given h is infeasible to find M
weak collision resistance: given x is infeasible to find y, so that H(y) = H(x)
strong collision resistance: is infeasible to find any x, y so that H(y) = H(x)

Security

每个抗碰撞的哈希函数H都有一个固定的输出长度「Hash Output Length」。

为了用暴力攻击破解 H 的（强）抗碰撞性，对手反复选择随机值 x，计算H(x) 并检查散列函数是否等于所有先前选择的随机值的任何一个散列值。

如果 H 的输出是 N 比特长，在发现碰撞之前，对手需要尝试的预期次数是多少？

问题：假设H的输出是 80 比特长，对抗者必须尝试多少个值才能使抗碰撞的概率至少为 1/2 ？=> 2 ⁴⁰

这表明，安全的 N 位散列需要 2 ^N/2 的尝试来 "破解"（就抗碰撞而言），平均而言。

Brute force Attack Against the Collision- resistance of a Hash Function

10 位消息摘要非常不安全，因为在进行略微超过 25（即 32）次随机散列后，发现一次冲突的概率至少为 0.5
40位信息摘要也是不安全的，因为在做了略微超过220个（约一百万）的随机哈希后，可以发现碰撞的概率至少为0.5。

Block Ciphers as Hash Functions

将输入消息划分为固定大小的块
输入的剩余位被填充以信息长度的值

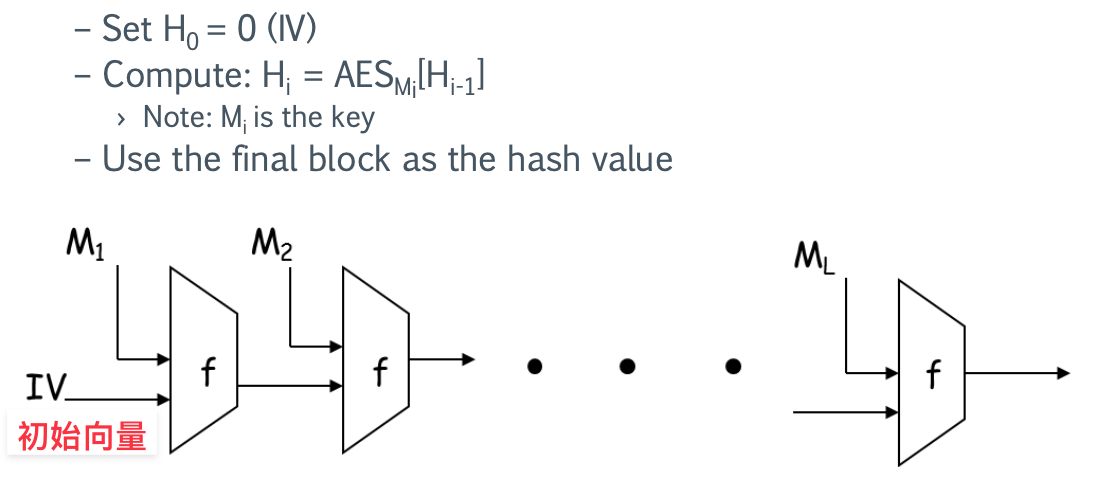
初始化：选择一个初始值IV（初始向量），其长度等于分组密码的块长度。
迭代处理：将填充后的数据分成大小相等的块。对于每一个数据块，将其与上一个块的散列值进行某种操作（如异或），然后使用分组密码加密算法（如AES）对结果进行加密。将加密后的结果作为下一个块的散列值。对于第一个数据块，使用初始向量作为散列值。
输出：在处理完所有数据块后，最后一个加密结果作为散列函数的输出。

Popular Crypto Hashes

Popular Crypto Hashes
- 128-bit output
- In Aug 2004, Wang「王小云」, et al. showed that it is “easy” to find collisions in MD5. They found many collisions in very short time (in minutes)
SHA-1 - A US government standard (similar to MD5)
- 160-bit output
- 2005年2月，Wang等人表明，在SHA-1中可以发现碰撞，估计需要花费269次哈希计算。
SHA-2 (SHA 256/384/512)
- Based on SHA-1 with a longer hash value
- 对于要求底层哈希函数应该是抗碰撞的应用，是时候从SHA-1迁移了。
- Start using the standards SHA-256 and SHA-512

Basic Cryptography III

# Basic Cryptography III

# Symmetric Key Management

# Centralized Key Management

# Public Key Encryption

# Motivation of Public Key Crypt

# RSA Encryption Algorithm

# RSA 原理

# Example

# Security

# Problem of Public-Key Crypt

# Comparison

# Merkle’s Secret Key Distribution

# Diffie–Hellman Exchange

# Digital Signatures

# Basic Model

# RSA Signature Scheme

# Hash Signature Scheme

# Hash Function

# Requirements for Hash Functions

# Security

# Popular Crypto Hashes

Basic Cryptography III

Symmetric Key Management

Centralized Key Management

Public Key Encryption

Motivation of Public Key Crypt

RSA Encryption Algorithm

RSA 原理

Example

Security

Problem of Public-Key Crypt

Comparison

Merkle’s Secret Key Distribution

Diffie–Hellman Exchange

Digital Signatures

Basic Model

RSA Signature Scheme

Hash Signature Scheme

Hash Function

Requirements for Hash Functions

Security

Popular Crypto Hashes