Basic Cryptography II
Basic Cryptography II
Modern Symmetric Ciphers
「现代对称密码」:现代对称密码处理的是二进制比特级的信息
10010011111011101
两种主要方法: Stream Ciphers「流密码」, Block Ciphers「块密码」
Stream Ciphers
流密码是一种加密算法,它一次处理一个比特或以称为 "块 "的小单位处理数据。
- 它使用对称密钥,这意味着加密和解密都使用同一密钥。
- 密钥被用来生成一个伪随机比特或字节流,然后用比特XOR操作将其与明文相结合。(每次加密和解密都是基于一次密钥流产生的密钥流与明文进行异或运算得到密文)
- 由此产生的密码文本通过通信渠道发送,并可通过使用相同的密钥和程序进行解密。
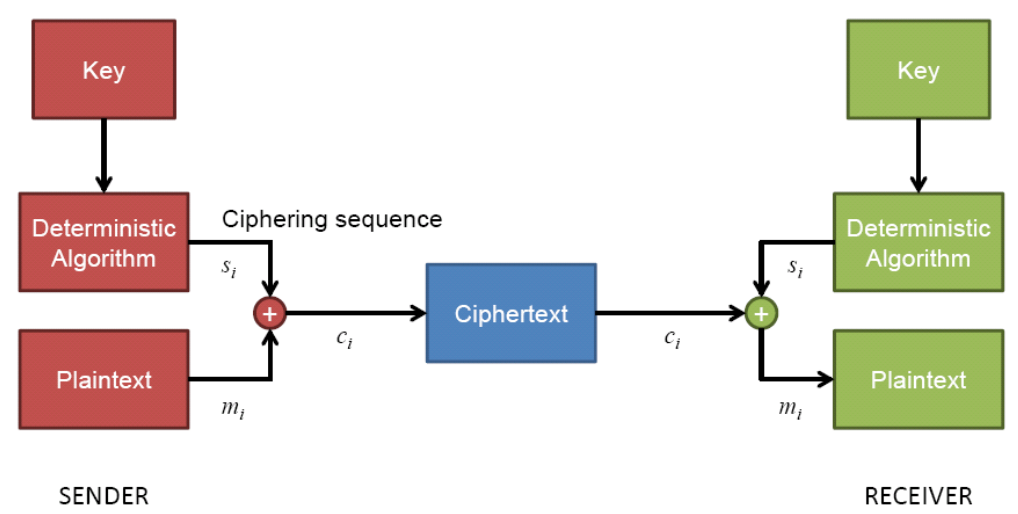
流密码经常被用于需要快速加密和解密数据的应用中,如网络电话(VoIP)和即时通讯(IM)应用。
- Secret key length: 128 bits, 256 bits, etc.
- 最大明文长度:通常可以任意长
- Synchronous vs Asynchronous
- Security
- 无法推出密钥
- 无法推导出密钥流的后续内容/后续密钥
Example: ChaCha20 in TLS 1.3
ChaCha20是一种非常安全和高效的密码学安全算法,因此可以被用于生成密钥来保护加密通信的安全性。它的作用是生成一个伪随机的密钥流,生成的密钥更像是随机的。可以用于加密和解密数据。
The input is packaged as a 512-bit block

- Use a 256-bit key
- A word is length is 32
- Divided into to 8 * 32-bit words
- Other input
- 4 words: constants
- 2 words: a nonce
- 在解密时,也需要使用相同的 Nonce 值
- 2 words: a block counter
- 每次加密时增加1
- Output: 256 bit keys
生成秘钥时,每轮迭代都会进行下列四步操作:
- 每 4 个字节(32 位)作为一组,分别进行加法模 2^32 运算,得到新的 4 字节。
- 将每个字节对应的 32 位数值进行一系列的按位异或、按位左移、按位右移等运算,得到新的 4 字节。
- 将每个字节对应的 32 位数值进行一系列的按位异或、按位左移、按位右移等运算,得到新的 4 字节。
- 将新得到的 4 字节与原来的 4 字节相加,得到新的 4 字节。
加密和解密过程
- 输入秘钥和随机数
- 通过一系列的置换运算和加法运算,生成一个密钥流。
- 将密钥流与明文进行异或运算,得到密文。
- 对密文进行相同的异或运算,得到明文。
ChaCha20 采用了简单的结构和高效的算法,具有很高的安全性和速度。它已被广泛应用于各种加密应用中,例如 HTTPS、TLS、SSH 等。
流密码算法的设计注意事项
- 一个确定的函数,产生一个最终会重复的比特流。-> 加密序列应该有一个大的周期
- 在ChaCha20中,2个字的计数器允许一个大的周期
- 密钥流应该尽可能地接近真正的随机数流的特性。
- In ChaCha20, the quarter-round functions allows a high diffusion
- 密钥应足够长,以抵御暴力攻击「brute-force」
- In ChaCha20, it is 256 bits
Block Ciphers
Block Ciphers 是另一种类型的加密算法
- 信息被分解成固定大小的块
- It is encrypted, one block at a time
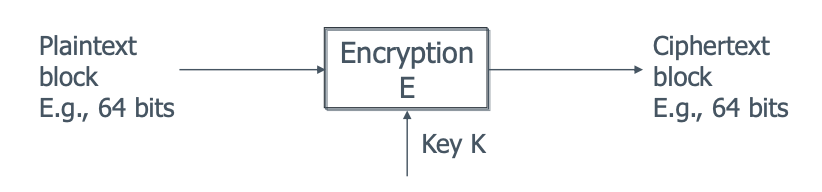
- 对固定大小的数据块进行操作,通常长度为 64 或 128 比特。
- 与流密码一样,区块密码在加密和解密时都使用对称密钥。
- 与流密码不同的是,Block Ciphers 是以块为单位处理数据,而不是一次一个比特。
- Block Ciphers 通常使用复杂的数学运算,如替换和置换,将明文篡改为密文。
Choice of Block Size
- Small block size may be insecure
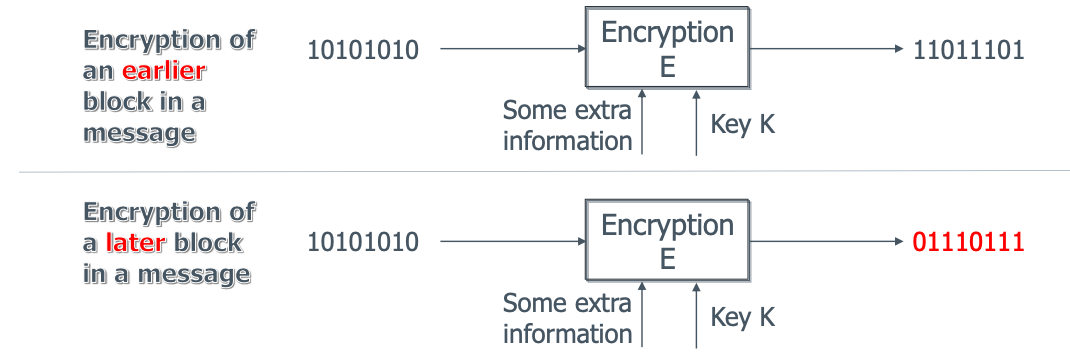
- 相同的明文块总是产生相同的密文块
- 8位块大小只有256个值 -> 用频率分析来破解!
在实践中,加密算法被设计为确保所有后续区块产生的密码文本与之前的加密文本不一致。
Block Cipher Principles
- 大多数对称 Block Cipher 都是基于 Feistel 密码结构的
- Block ciphers look like a large substitution
- a table of 2^64 plaintext-to-ciphertext entries for a 64-bit block
- Create the ciphertext from smaller building blocks
Confusion and Diffusion
- Cipher 需要完全隐藏原始消息的统计属性「statistical properties」
- A one-time pad does this perfectly
- 更实际的是,香农建议将各种元素结合起来,以获得
- Diffusion「扩散」: 将明文的统计结构消散在大量的密码文本,缓解了由于重复使用密钥而暴露统计特征的向题。
- 即使得明文与密文之间的关系复杂化。
- Confusion「混淆」: 使得密文和密钥之间的关系尽可能地复杂化
- Diffusion「扩散」: 将明文的统计结构消散在大量的密码文本,缓解了由于重复使用密钥而暴露统计特征的向题。
换句话说,密码文本中的每一个比特都应该依赖于明文和密钥中尽可能多的比特。
Feistel Cipher Structure
Feistel 密码结构是一种块密码设计方法。它将明文块分成两个相等的部分,并通过一系列迭代轮函数来加密明文。
- 在每轮中,其中一个明文部分通过某种函数(称为轮函数)和另一个明文部分进行混合和变换
- 然后与另一个明文部分进行异或运算
- 最后,这两个部分被互换,以便在下一轮中使用另一个轮函数。
它实现了香农的 substitution-permutation network 概念。
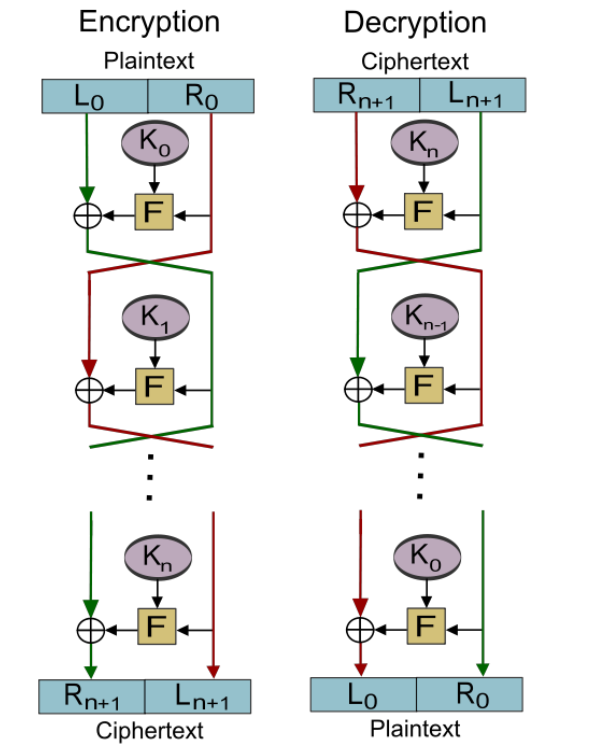
加密和解密过程
下面是 Feistel 密码结构的一个简单示例,其中明文长度为 8 个比特,密钥长度为 10 个比特,使用 2 轮迭代轮函数:
将 8 个明文比特分成左半部分 (L) 和右半部分 (R):L0R0
对于每轮迭代,应用以下步骤:
a. 通过将右半部分 (Ri) 与当前轮的密钥 (Ki) 进行异或,生成一个临时值 (Ti):Ti = Ri ⊕ Ki
b. 将临时值 (Ti) 传递到一个称为轮函数 (F) 的函数中,以生成一个新的临时值 (Ui):Ui = F(Ti)
c. 将新的临时值 (Ui) 与左半部分 (Li) 进行异或,生成新的右半部分 (Ri+1):Ri+1 = Li ⊕ Ui
d. 将旧的右半部分 (Ri) 移动到左半部分 (Li+1):Li+1 = Ri
在最后一轮中,左半部分 (L2) 和右半部分 (R2) 互换位置,生成加密后的密文:Ciphertext = R2L2
下面是一个具体的 Feistel 加密示例,其中明文为 01101101,密钥为 1011011100,使用 S-Box 和 P-Box 轮函数。假设使用 2 轮迭代。
将明文分成左右两个部分:L0 = 0110, R0 = 1101
对于第一轮迭代:
a. R0 ⊕ K1 = 1101 ⊕ 1011011100 = 1000001101
b. F(1000001101) = 00110111 (S-Box 和 P-Box 轮函数的结果)
c. L0 ⊕ 00110111 = 01100110 (R1)
对于第二轮迭代:
a. R1 ⊕ K2 = 01100110 ⊕ 1011011100 = 11010010
b. F(11010010) = 00111010
c. L1 ⊕ 00111010 = 01011100 (R2)
最后将 R2 和 L2 互换位置,得到密文:C
解密过程与加密过程类似,只不过需要使用相同的密钥,并将轮密钥的使用顺序反转。下面是针对之前加密示例的解密过程:
将密文分成左右两个部分:L2 = 1101, R2 = 0101
对于最后一轮迭代,右半部分 (R2) 变成左半部分 (L1),左半部分 (L2) 变成右半部分 (R1):L1 = 0101, R1 = 0110
对于第二轮迭代:
a. R1 ⊕ K2 = 0110 ⊕ 1011011100 = 11010110
b. F(11010110) = 10011101
c. L1 ⊕ 10011101 = 11001000 (R0)
对于第一轮迭代:
a. R0 ⊕ K1 = 11001000 ⊕ 1011011100 = 01111100
b. F(01111100) = 10010010
c. L0 ⊕ 10010010 = 11110111 (R0)
最后将 R0 和 L0 互换位置,得到明文:01101101,与加密前的明文一致。
Feistel Cipher Design Principles
- Block size: 增加大小可以提高安全性,但会减慢密码
- Key size: 越来越大的体积提高了安全性,使详尽的密钥搜索更加困难,但可能会降低密码的速度。
- Number of rounds: increasing number improves security, but slows cipher
- Subkey generation「子密钥生成」:更大的复杂性会使分析更难,但会减慢密码
- 快速软件加密/解密和易于分析: are more recent concerns for practical use and testing
Subkey
子密钥「轮秘钥」在 Feistel 密码结构中被用于对每个轮函数的输入进行加密。每个子密钥与每个轮函数的输入长度相同。
主密钥通常会通过某种密钥派生函数进行处理,以生成每个子密钥。常见的密钥派生函数包括哈希函数和密码学安全的伪随机数生成器。
在加密过程中,轮密钥按顺序应用于每个轮函数中。具体来说,第 i 个子密钥将用于对第 i 轮轮函数的输入进行加密。在解密过程中,轮密钥应该按相反的顺序应用于每个轮函数中。
Data Encryption Standard
- A block cipher
- Both plaintext and ciphertext are 64 bits
- Key: 64 bits (56-bit effective key)
通过一系列的替换「substitution」和移位(或排列)「换位(或排列)」进行加密。
Round Function Analysis
比如一个 32 位的数据
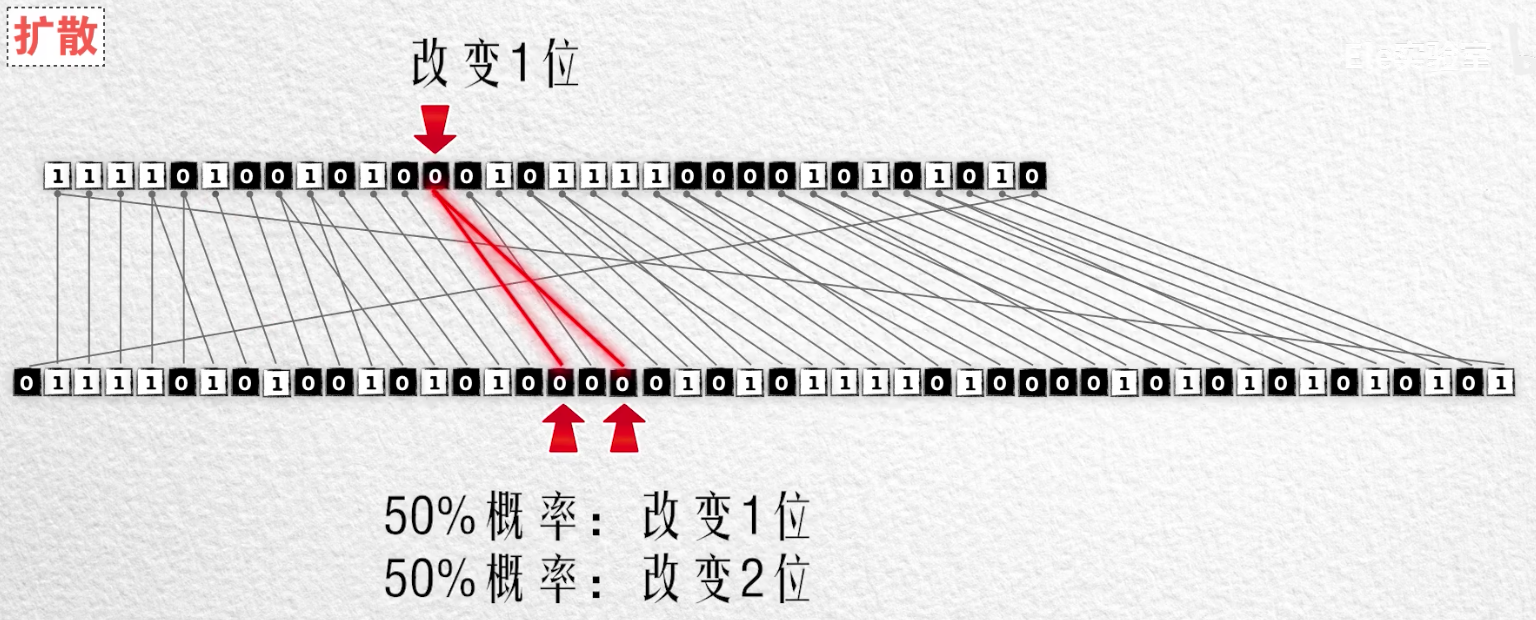
- 选择其中的16位让它们扩散为2位,形成一个48位的数据
- 这样改变输入数据的一位,就有一半的概率导致输出数据两位的变化
- 然后让扩散后的数据和一个48位的密钥进行异或
- 接下来再使用香农给出的第二个方法:混淆
- 将扩散并和密钥异或后的48位数据分成6位一组
- 使用一张这样的表格
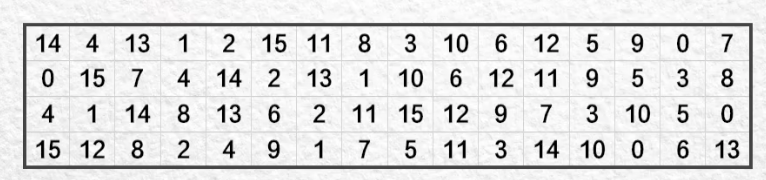
- 取第一位和最后一位组成一个两位二进制数指定表格的行号
- 中间的四位二进制数指定表格的列号
- 如此便从这个表格中取出了对应的数字,再将这个数字转化位为4位2进制数
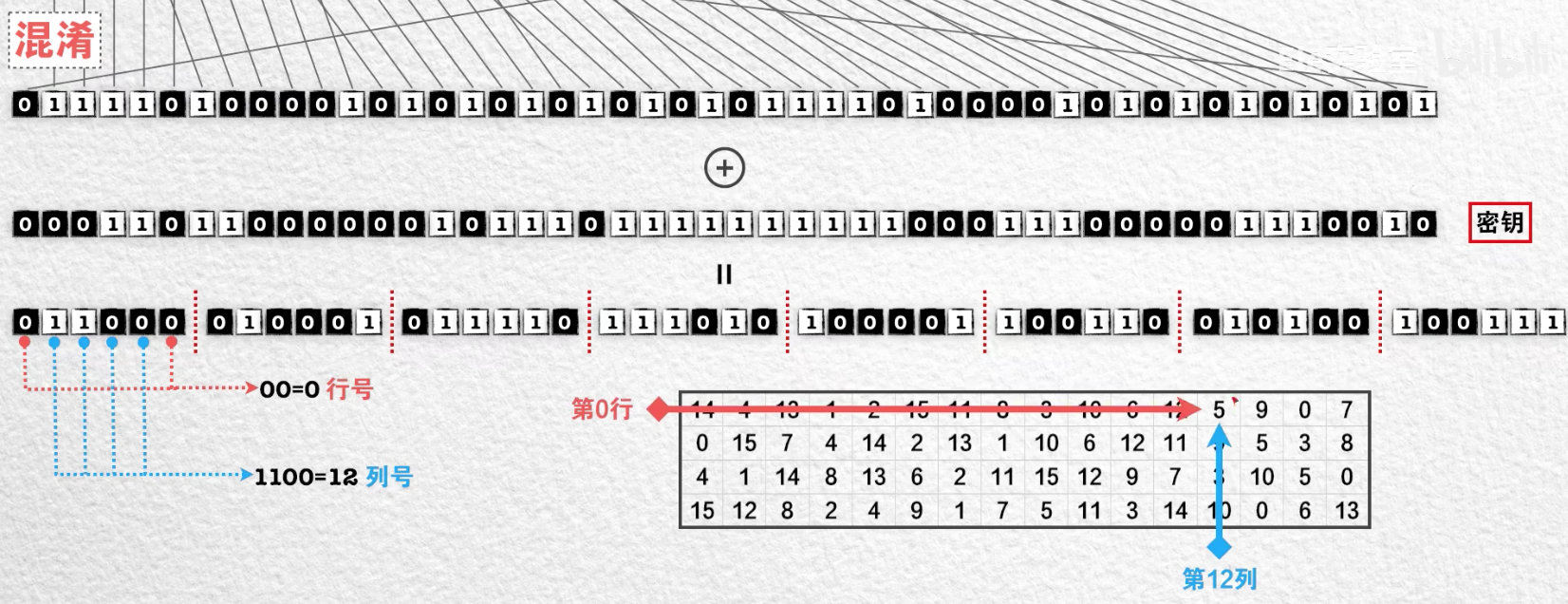
- 之后的每一组,都换用不同的表格,用同样的方法取出表格中的一个数字
- 8组6位数经过8个不同的变换表格得到了8组4位数
- 再将结果合并成一个32位的数
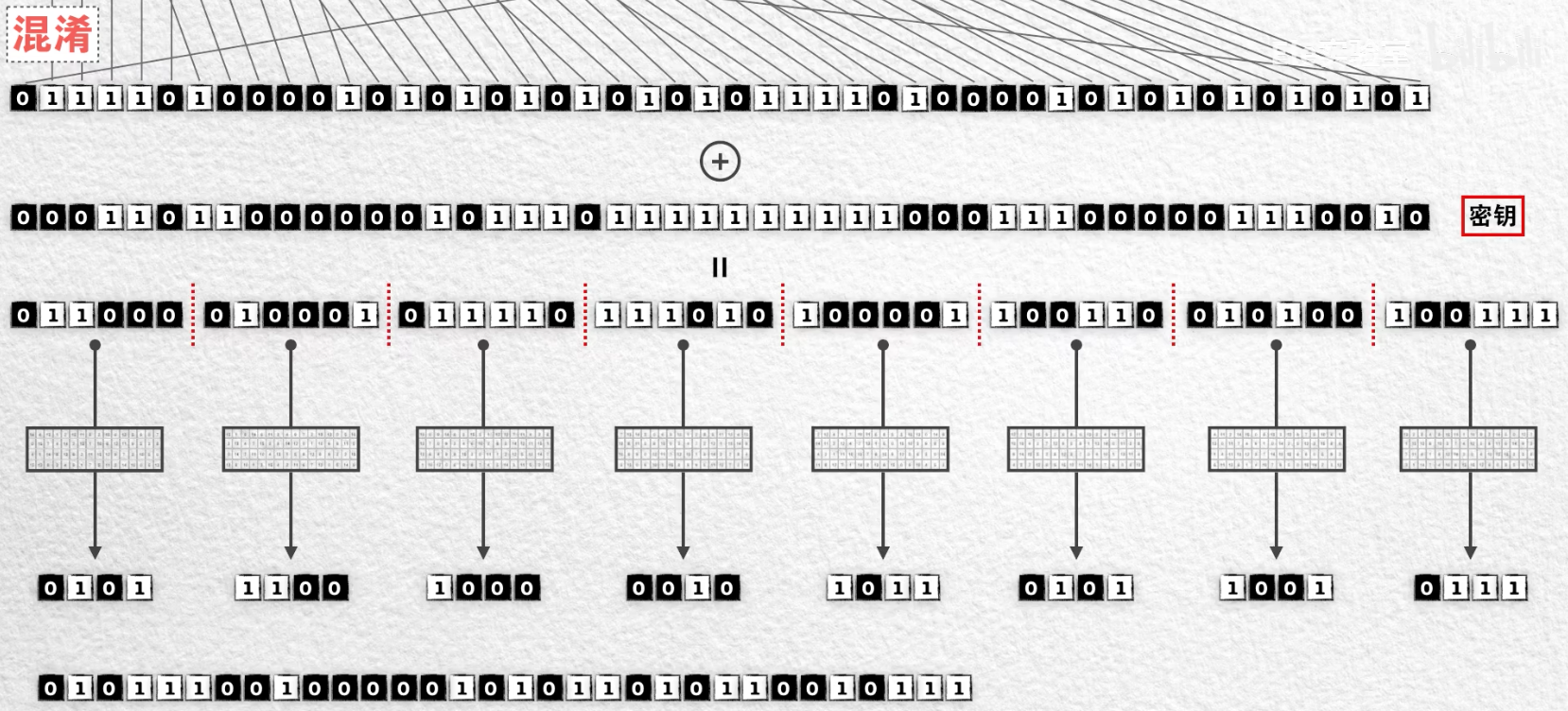
以上就是 DES 算法的核心部分。其中这用于转换的表格,称为 s 盒。
混淆以后的 32 位数据还进行了一次随机置换的操作,再次打乱了结果。

总结下来就是,先将明文分组扩散,再和秘钥异或,然后进行一次混淆(依赖 s 盒)。这几个操作结合起来,就是 DES 中的轮函数。
Input of DES
- Data: Need to be broken into 64-bit blocks; add pad at the last message if necessary
- E.g.,X=(35077F10AB12FC65)HEX
- Secret key: 任何 64 位长的字符串,包括 8 个奇偶校验位
- 钥匙的每个8位字节中的1个奇偶校验位可用于钥匙生成、分发和存储中的错误检测。
- K = (k1 ... k7 k8 ... k15 k16 k17 ... k24 ... k32 ... k40 ... k48 ... k56 ... k64)

DES Encryption
DES 规定数据一共经过 16 轮这样的轮函数,依次将上一轮的输出作为下一轮的输入。
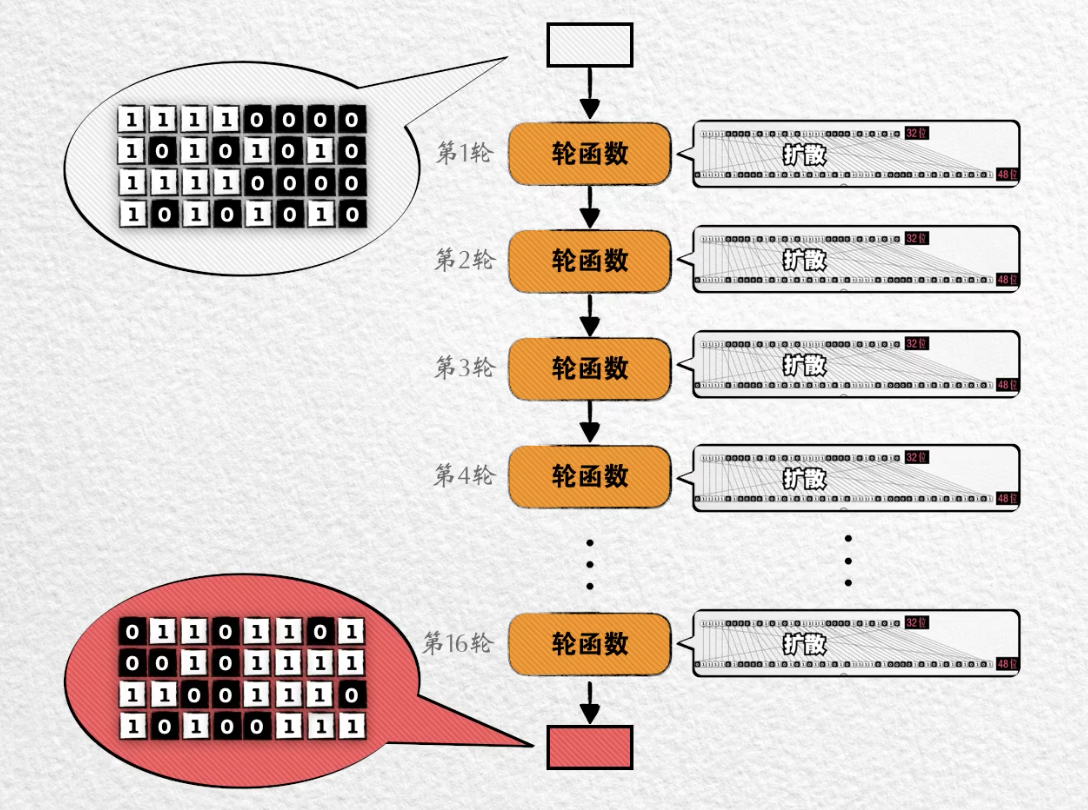
数据经历轮函数中的一次扩散后,改变一位输入会有一半的机会政变两位输出,缓解了密文中暴露统计特征的问题。
- 每一轮都会将明文一位变化所影响的位数扩大,16次后,你将发现输入的一位改变将起输出许多位的改变。这让明文和密文之间的关系变得极其复杂。
- 同时经历16轮的16次非线性变换(混淆),使得密文和密钥之间的关系尽可能地复杂化。
解决了单独使用 异或 存在的问题。
位数
首先,DES 的密钥是 64 位, 而其中有8位完全无效(奇偶校验位)。即只有56位有效秘钥。而这 16 轮轮函数每一轮都需要一个不同的48位的密钥
首先,对这56位密钥按位进行一次顺序置换,再把他们分为各28位的两个部分
- 然后对这两个部份各自循环左移一位,得到两个新的28位
- 对新的两个28位再各自循环左移1位,得到两个新的28位
- 再对新的两个28位各自循环左移两位,得到两个新的28位
- ...
按照这16个左移位数的指示, 完成这样的左移操作,就得到了16个28位。
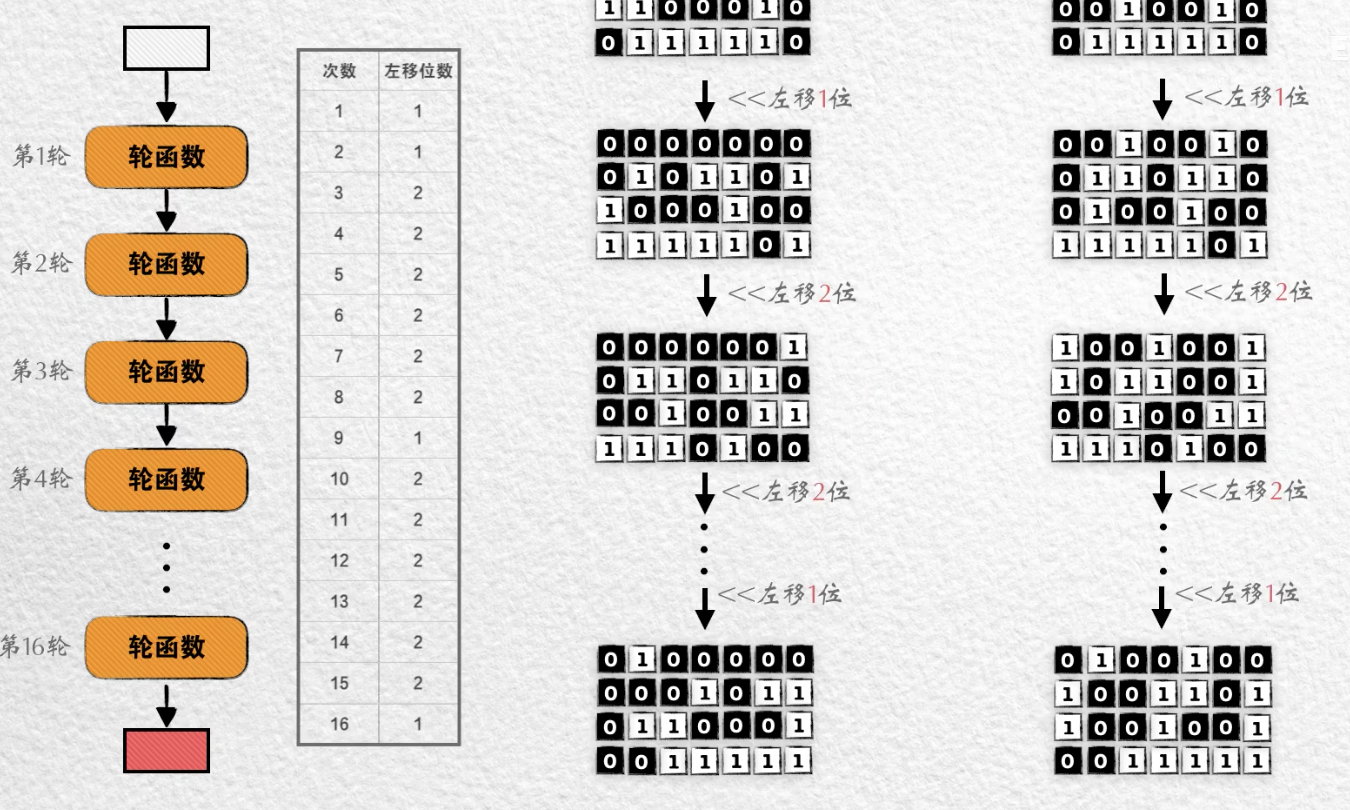
再把这16对数各自合并,就得到了 16个 56位的数据。从56位中选出48个。
如此我们就得到了用于 16轮 加密的16个48位的密钥。
DES 算法中的明文分组长度其实是64位而不是32位,在加密开始阶段会将其分为各32位的左右两部分,这两部分数据是这样完成16轮轮函数计算的:
- 首先将右半部分送入轮函数
- 计算结果再与左边半部分异或,作为下一轮的右半部份
- 再把右半部分直接拿过来作为下一轮得左半部分
- ...
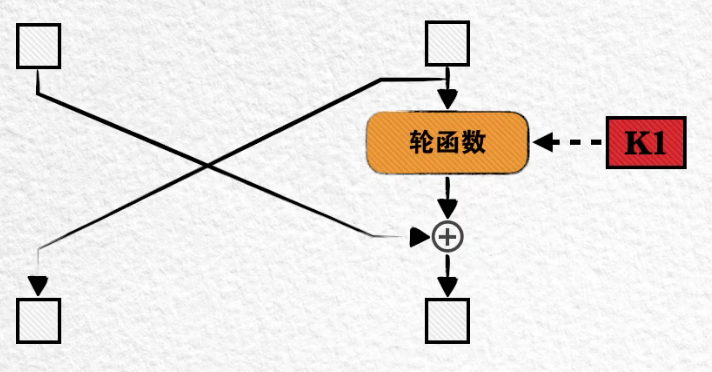
最后再把左右交换一下位置,就得到了一个64位的输出。
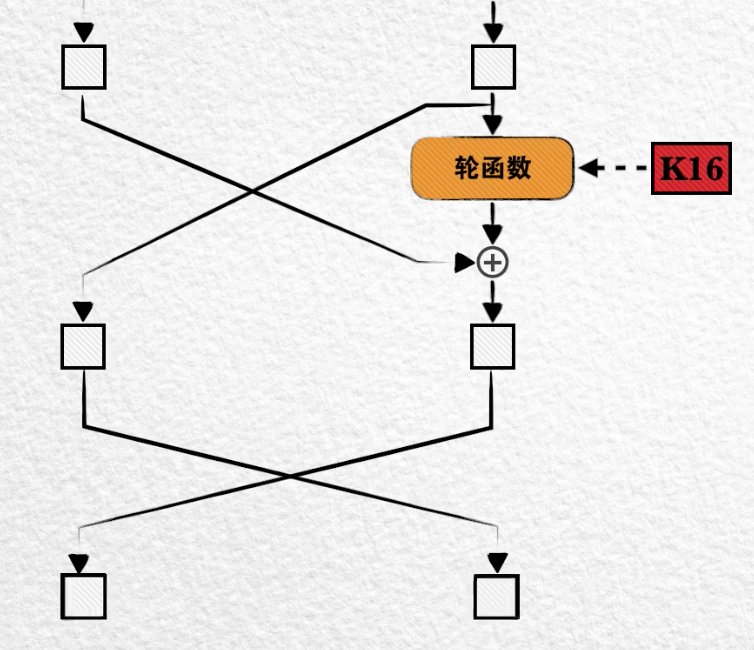
DES 算法 在明文分组输入后 和 密文分组输出前,都 附加了一个随机置换的操作进一步扰乱数据。
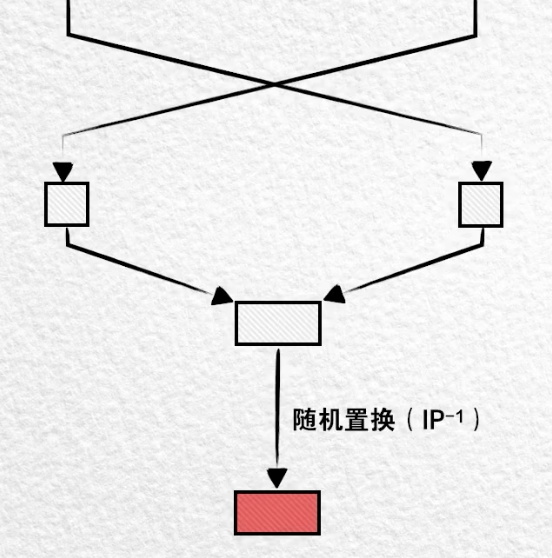
如此我们最终便得到一个64位的密文分组。
DES Decryption
对称算法,加解密使用同一个密钥。只需要将这16个轮密钥颠倒一下顺序,再做一次加密的过程,就可以得到明文。
S-box Mapping misunderstanding
问题是这样的:如果将 6 位映射到 4 位,则会丢失信息。因此,可能有不止一个 6 位组合映射到相同的 4 位组合。因此,在 S-box 操作之后,对我来说似乎不可能从 4 位结果中再次获得原始的 6 位。那么怎么可能再次解密你的密文呢?
原因在于,没有理解 S-box 的工作原理:好问题,是的,似乎数据会丢失。从技术上讲,有些东西显然必须消失,因为6不会进入4。但考虑到DES的整体架构。
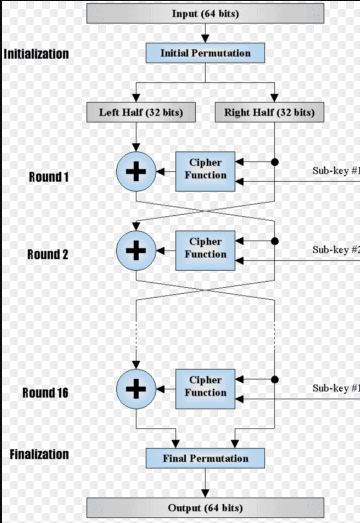
追踪一个单独的数据块的左右两半的流动。你会看到两个完整的32位字在Feistel网络中畅通无阻地流动。在那里没有信息丢失,只是被XOR了一下,保持了宽度。因此,64位进入块中,64位出现。
Today Usecase
- AES (Advanced Encryption Standard)
- has 128/192/256-bit keys, 128-bit data
- Supported by in SSL/TLS (HTTPS)
More on Block Cipher
区块密码将一个区块的明文作为输入,输出一个区块的密文。它通常被看作是一种伪随机的排列组合。
- What should we do if the message length is more than 1 block?
- 如果信息长度不是区块的倍数,我们应该怎么做?例如,如果明文是129位,我们如何用 DES 加密?
为了处理第一个问题,已经制定了不同的操作模式
- Electronic codebook mode
- Cipher block chaining mode
- Cipher feedback mode
- Output feedback mode
- Counter mode
至于第二个问题,可以考虑 Padding「填充」.
- 我们需要应用一个填充规则,使最后一个区块得到适当的加密。
- 填充是指在区块的末尾添加一个固定的 1 和 0 的图案,这很容易与实际信息区分开来。
Example:
- Add a string 1000...0 to fill out the last block to the correct length
- 对于解密,将明文视为被读回的最小有效位,即为1
- 如果明文已经是区块大小的倍数,可能需要添加一个新的区块,以避免产生歧义。
对于 CTR 模式,可以简单地仅使用最后一个输出块的最高有效 u 位进行 XOR 运算 -> 这揭示了消息的长度,这并不总是可取的。
Electronic Codebook (ECB) Mode
The basic mode of operation -> 信息的每个区块都是单独加密的
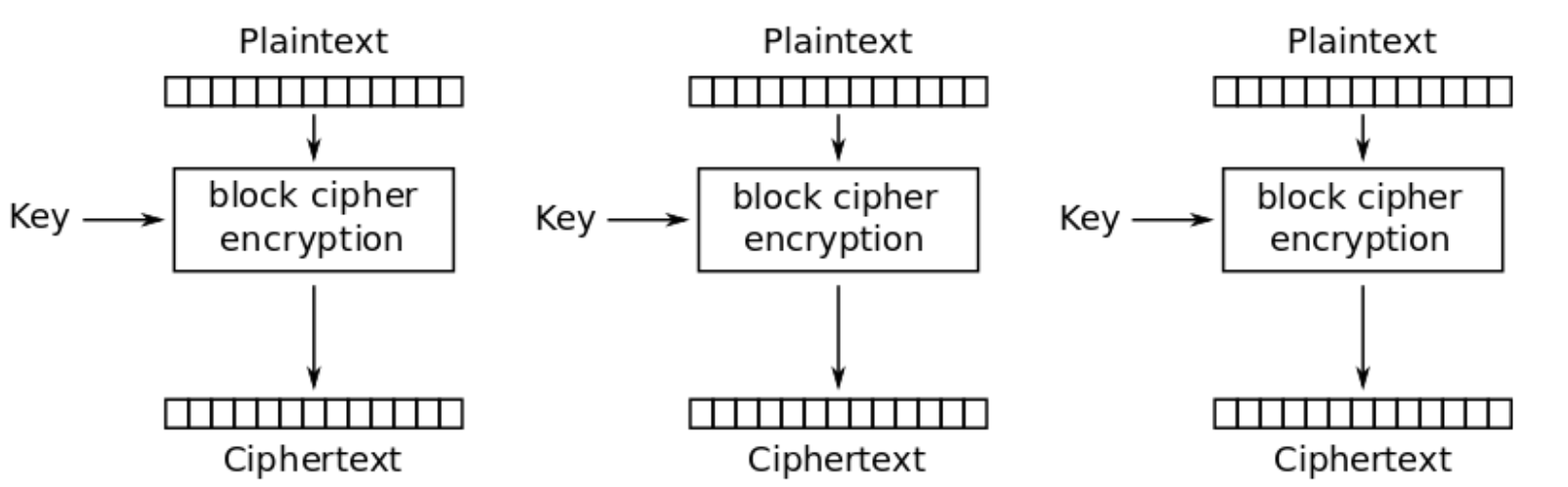
ECB 模式会泄露有关明文的信息,因为相同的明文块会产生相同的密文块。密文不应该泄露任何关于用于创建它的明文的信息,所以ECB 模式是不安全的,不应该被使。参考统计学概率。
Cipher Block Chaining (CBC) Mode
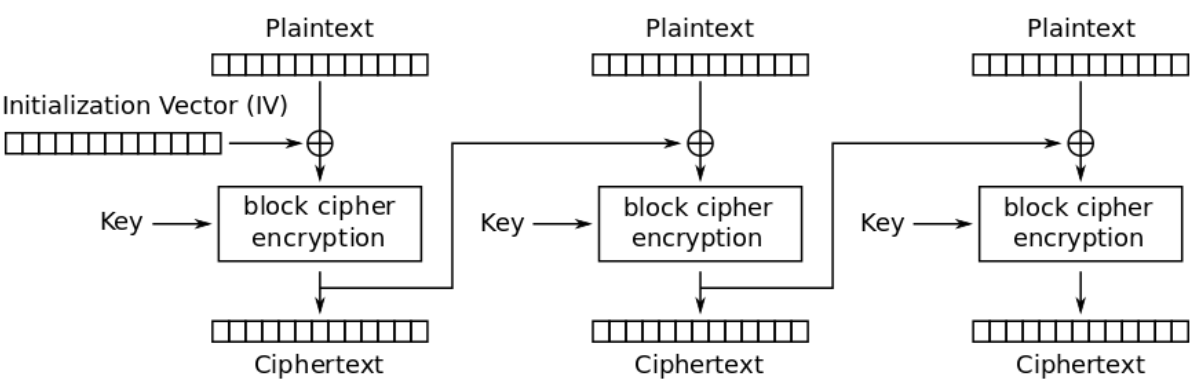
Cipher Feedback (CFB) Mode
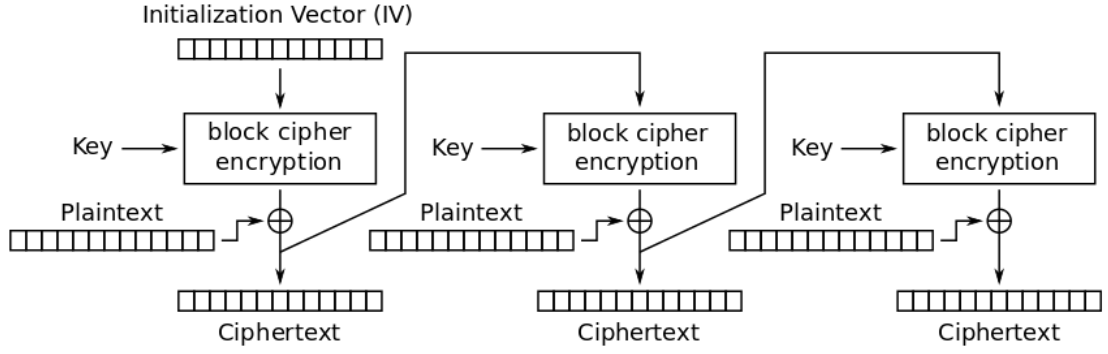
OFB Mode Encryption
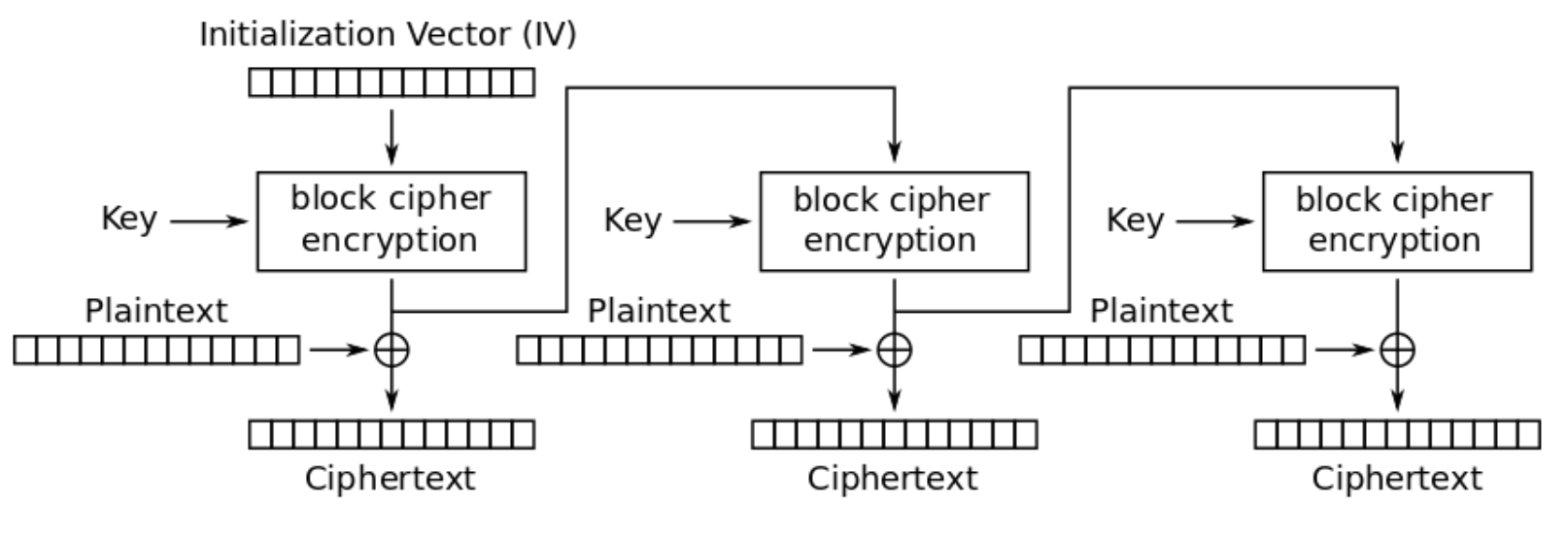
Counter (CTR) Mode