跳至主要內容

Crypto Math

Hirsun大约 29 分钟

Crypto Math

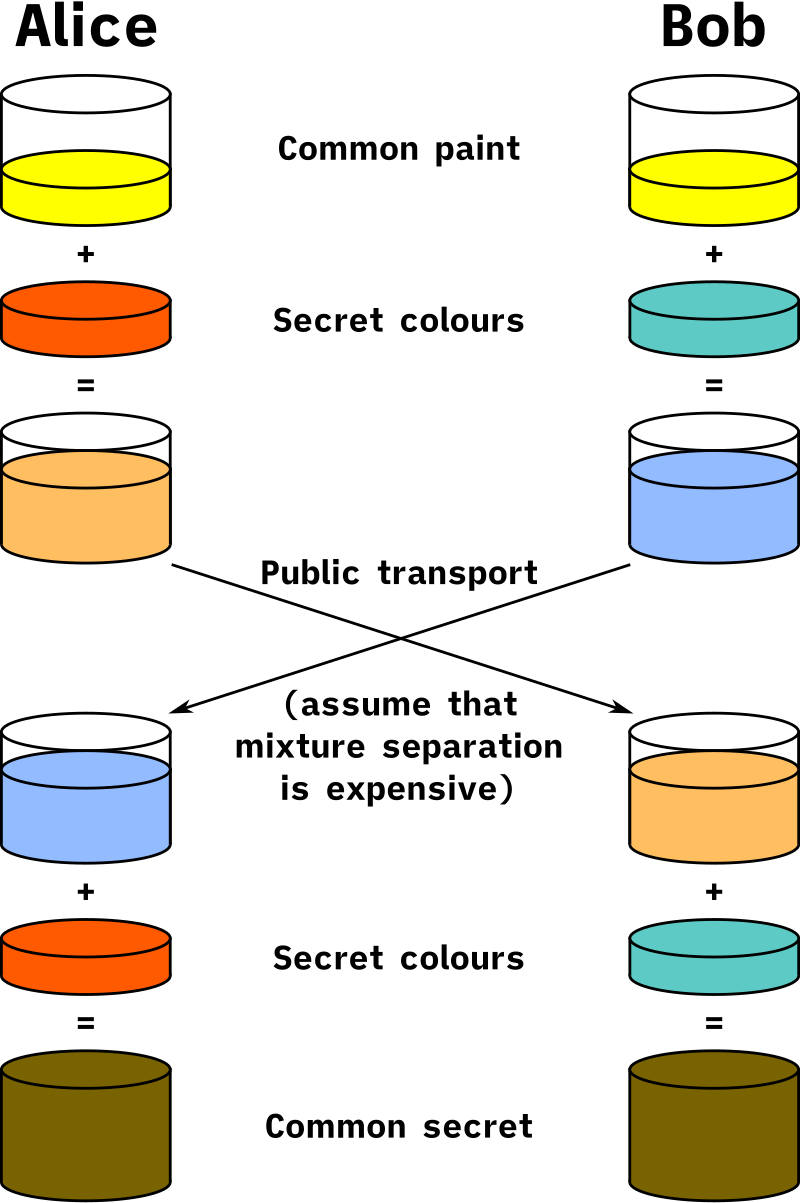
Diffie-Hellman Protocol

Diffie-Hellman_Key_Exchange.svg.png

提示

离散对数问题是指在给定一个大质数p和一个基数g的情况下，找到一个整数x，使得g^x ≡ y (mod p)。这个问题被认为在计算上是困难的，Diffie-Hellman协议的安全性正是基于离散对数问题的难度。

Diffie-Hellman协议是公钥加密的“种子”，另一个重要的分支是RSA加密算法。

Example:

Alice和Bob希望在公开的互联网信道上安全地交换一个共享的秘密密钥，以便后续使用对称加密进行安全通信。

在公开信道上交换密钥时，存在被攻击者监听的风险。Diffie-Hellman协议通过数学方法确保即使通信被监听，攻击者也无法得知密钥的具体内容。

  1. Alice和Bob选择一个大质数p和基数g，并公开这些值。
  2. Alice生成一个随机数a，并计算A = g^a mod p，然后将A发送给Bob。
  3. Bob生成一个随机数b，并计算B = g^b mod p，然后将B发送给Alice。
  4. Alice计算共享密钥S = B^a mod p。
  5. Bob计算共享密钥S = A^b mod p。
  6. 因为S = g^(ab) mod p，Alice和Bob得到了相同的共享密钥。

假设p = 23, g = 5。

  • Alice选择a = 6，计算A = 5^6 mod 23 = 8。
  • Bob选择b = 15，计算B = 5^15 mod 23 = 19。
  • Alice计算共享密钥S = 19^6 mod 23 = 2。
  • Bob计算共享密钥S = 8^15 mod 23 = 2。
    最终，Alice和Bob得到了相同的共享密钥2。

Discrete Logarithm Problem

离散对数问题（DLP）：已知 p、 g 和 g^x mod q ，计算 x 是困难的。这里的破是一个大素数， g 是生成元， g^x mod q 是已知结果， x 是我们需要计算的未知数。由于计算离散对数的复杂性，求解 x 是困难的。

具体来说，如果我们有一个素数 p，和一个生成元 g，以及一个数 y，使得 y=g^x mod  p，那么 x 就是 y 以 g 为底的离散对数。计算离散对数 x 是一个复杂的问题。

DL 假设（假设离散对数问题是困难的）是安全性的必要条件。也就是说，我们假设计算离散对数是非常困难的，这个假设是许多加密算法安全性的基础。

什么是“困难的”？在加密学中，“困难的”通常意味着计算量非常大，以至于在合理的时间内无法计算出结果。

暴力破解（brute-force attack）是一种尝试所有可能的密钥组合以找到正确密钥的方法。在离散对数问题中，暴力破解是不可行的，因为可能的组合数量非常大。

Example

假设我们有一个大素数 p=23，生成元 g=5，和 g^x mod  p= 4。我们需要计算 x。

1730281455861.png

Definition Notation

对于一个正整数 n 和任意整数 a 和 b。

  • a | b 表示 a 能整除 b，即存在一个整数 t，使得 b = ta。
  • gcd(a, b) 表示 a 和 b 的最大公约数。例如，gcd(8, 12) = 4。
  • 如果 gcd(a, b) = 1，则 a 和 b 互为质数，即 a 和 b 没有其他公约数，除了 1。注意，a 或 b 本身不一定是质数。
  • Zₙ 表示模 n 的整数集合，即 {0, 1, 2, ..., n - 1}。这是一个环结构。
  • 模运算表示 a 除以 n 的余数。a % n 和 a mod n 都表示这个余数，结果 r 属于 Zₙ。即 n 能整除 (a - r)。
  • a ≡ₙ b 表示整数 a 和 b 在模 n 下同余。
  • a 和 b 在模 n 下同余的两个等价条件：a % n = b % n；或 n 能整除 (a - b)。
  • n 被称为模数。
  • 如果模数在上下文中是明确的，可以省略 mod n 或 ≡ₙ 中的 n。
  • 在模运算中，符号 ≡ 表示同余关系。
    • 具体来说，两个整数 a 和 b, 如果它们除以 n 的余数相同, 则被称为在模 n 意义下同余
    • 数学上记作 a ≡ b mod n, 或者 a ≡n b
    • 这意味着 n 整除 a−b，即 (a-b)/n 是整数
    • 2 * 8 ≡ 1 mod 15 表示 2 * 8 / 15 = 1

求最大公约数

给定两个整数 56 和 98，求它们的最大公约数，

  1. 分解因数：56 = 2^3 × 7，98 = 2 × 7^2。
  2. 找出共同的因数：2 和 7。
  3. 取最小次幂：2^1 × 7^1 = 14。

因此，gcd(56, 98) = 14。

Modular Addition & Multiplication

  • 一个数的加法逆元是在模运算下加上该数可以得到零的数。
    • 例如，在 mod 9 下，2 的加法逆元是 7，因为 2 + 7 = 9 mod 9 = 0。
  • 一个数的乘法逆元是在模运算下乘以该数可以得到 1 的数。
    • 例如，在 mod 9 下，2 的乘法逆元是 5，因为 2 * 5 = 10 mod 9 = 1。
    • 乘法逆元是否总是存在？答案是否定的，只有当两个数互质时，乘法逆元才存在。
  • 两个数互质是指它们的最大公约数为 1。
    • 例如，3 和 4 是互质的，因为它们的最大公约数是 1。互质性在确定乘法逆元时非常重要。

除法计算 （除法的含义）

计算 9 / 2 ≡15 的结果

  • 首先，我们找到 2 的模 15 的逆元, 即 2x mod 15 = 1, x = 8
  • 9 / 2 ≡15 等价于 9 * 8 ≡15, 即 (72 - x) / 15 为 的结果为整数
  • 可知 x = 12

在模 15 的运算中，将“乘以 8”解释为“除以 2”是合理的。这是因为在模 15 意义下，8 的逆元是 2。

在模 15 的运算中，2 和 8 有特殊的关系。具体来说，8 的逆元是 2，这意味着 8⋅2≡1mod  15。

没有这样的 y 存在！这意味着在模 15 意义下，5 没有逆元。

Extended Euclidean Algorithm

贝祖定理（Bézout's theorem）

  • 对于所有整数 x 和 y，存在整数 a 和 b，使得 ax + by = gcd（x,y）。
  • 这意味着我们可以找到一组系数 a 和 b，使得x和y 的线性组合等于它们的最大公约数。

我们可以使用扩展欧几里得算法

  • 30÷20=1余10（即30=1·20+10）
  • 20÷10=2余0（即20=2·10+0）

所以，gcd(30，20)=10

Groups

在一个有限「finite」集合G中，定义一个“群运算”（例如），

  • 如果对于任意的a和b在G中，a * b的结果也在G中，那么这个运算是封闭「closed」的。
  • 对于G中的任意元素a, b, c，(a * b) * c = a * (b * c)成立，这意味着运算是结合「associative」的。
  • 对于阿贝尔群（Abelian group），任意a和b在G中，a * b = b * a成立，这意味着运算是可交换的「commutative」。
  • G中存在一个单位元e，对于任意a在G中，e * a = a * e = a成立。
  • 对于G中的任意元素a，存在一个元素b使得 a * b = b * a = e成立，这意味着每个元素都有逆元素。

Examples:

  • 例如，整数集合Z在加法运算下是一个无限群「infinite」。
Example

假设我们有一个集合G = {0, 1, 2}，定义一个运算 *为模3加法，即a * b = (a + b) mod 3。验证这个集合G在运算 *下是否构成一个群。

我们需要验证G是否满足群的四个基本性质：封闭性、结合律、单位元和逆元。

  1. 封闭性：
    • 对于任意a, b ∈ G，(a + b) mod 3的结果仍然在集合G中。例如，1 * 2 = (1 + 2) mod 3 = 0，0在G中。
  2. 结合律：
    • 对于任意a, b, c ∈ G，(a * b) * c = (a + b) mod 3 + c mod 3 = a + (b + c) mod 3 = a * (b * c)。
  3. 单位元：
    • 0是单位元，因为对于任意a ∈ G，a * 0 = (a + 0) mod 3 = a。
  4. 逆元：
    • 对于任意a ∈ G，存在一个b使得a * b = (a + b) mod 3 = 0。例如，1的逆元是2，因为1 + 2 = 3，3 mod 3 = 0。

集合G = {0, 1, 2}在运算 *（模3加法）下满足群的所有性质，因此G在此运算下构成一个群。

Diffie-Hellman

Diffie-Hellman 协议的安全性依赖于离散对数问题「discrete logarithm problem (DLP)」的计算难度。

Schnorr Signature & Verification

假如

- 消息M = "Hello, Schnorr!"
- 私钥x = 3
- 公钥X = g^x = 2^3 = 8
- 生成元g = 2
- 随机数k = 5

步骤

1. 计算R = g^k = 2^5 = 32
2. 计算c = H(M, R) = H("Hello, Schnorr!", 32)（假设哈希值为7）
3. 计算s = k + cx = 5 + 7*3 = 26
4. 签名为(R, s) = (32, 26)

验证

1. 计算g^s = 2^26
2. 计算R * X^c = 32 * 8^7
3. 检查g^s是否等于R * X^c

重点关注

  • ECDSA的短签名大小，ECDSA中的公钥恢复：ECDSA的一个显著优点是其签名较短，这提高了效率。此外，公钥恢复技术在某些场景下非常有用。
  • BLS的美妙之处（例如，更短的签名）以及其他扩展性。BLS签名方案不仅提供了更短的签名，还具有其他扩展性，使其在某些应用中非常有吸引力。

Digital Signature Algorithm (DSA)

DSA，r是通过生成元g的k次幂对模数q取余得到的，s是k的逆元乘以H(m)加上x乘以r再对模数q取余得到的。

s中的“模数q”部分（涉及H(m)和r = g^k）起到了类似于Schnorr中H(M, R)的“转换函数”的作用。

这种设计“模糊”了可用于攻击的代数关系。

Elliptic Curve Discrete Logarithm Problem

椭圆曲线离散对数问题是指给定椭圆曲线上的两个点P和Q，找到一个整数k，使得Q = kP。这个问题在计算上是非常困难的，因此被用作密码学的基础。

椭圆曲线离散对数问题（ECDLP）被认为具有指数级的计算难度「指数级的计算难度」。

ECDSA是一种基于椭圆曲线的数字签名算法，用于验证消息的真实性和完整性。它广泛应用于现代加密通信中，如SSL/TLS协议。

RSA/factoring problem

暴力攻击「Brute-force attacks」尝试：暴力攻击是一种通过尝试所有可能的密钥组合来破解加密的方式。

对于RSA来说，这意味着尝试所有可能的私钥d，但由于d的范围很大，这种方法非常耗时。

所有可能的密钥 - d的范围越大，安全性越高，但解密速度越慢。

Comparison of Signature Lengths

1732305178158.png

Threshold Signing

  • 常规签名可能不够有用/灵活。
  • 效率、安全性、隐私。数字签名技术需要在效率、安全性和隐私之间找到平衡。

门限秘密共享是一种密码学技术，它将秘密分成多个部分，只有当达到某个门限时，才能重构秘密。

(t+1, n)门限签名：t+1个份额可以恢复私钥。

在门限签名方案中，私钥被分成n个份额，只有当获得至少t+1个份额时，才能恢复出完整的私钥。

一旦秘密被恢复，分享就变得没有意义了。这意味着，一旦私钥被恢复出来，分割成多个份额的意义就消失了，因为完整的私钥已经被重建。

Legends never die | Serving since 2011.
Copyright © 2025 Hirsun