Crypto Toolbox

Hirsun大约 79 分钟

Crypto Toolbox

Blockchain = {Security, Performance, Decentralization}

Topics

哈希（Hash）：哈希函数将输入数据转换为固定长度的哈希值，用于数据校验和加密。
认证数据结构/区块链（Authenticated Data Structure / Chain-of-Block）：通过哈希链将数据块链接在一起，确保数据的完整性和不可篡改性。
承诺（Commitment）：一种加密协议，允许一方在不泄露信息的情况下对某个值进行承诺，稍后再揭示该值。
签名（Signatures, e.g., ECDSA）：数字签名算法如椭圆曲线数字签名算法（ECDSA），用于验证消息的真实性和完整性。
公钥密码学（Public-Key Crypto）：使用公钥和私钥对进行加密和解密，确保数据安全性。
椭圆曲线密码学（Elliptic Curve Crypto.）：利用椭圆曲线数学结构进行加密，提供高效和安全的加密方法。
盲签名（Blind Signatures）：允许信息在未被签名者看到的情况下进行签名，确保隐私。
环签名（Ring Signatures）：允许一组用户中的任意一员代表整个组进行签名，而不透露具体签名者。
多重签名（Multi-Sig.）：需要多方共同签名才能完成交易，提高安全性。
后量子密码学（Post-Quantum Crypto., PQC）：针对量子计算机攻击设计的密码学方法，确保在量子计算时代的信息安全。
Cryptocurrencies「加墨货币」
- Cryptocurrencies: RingCT (Monero), Zerocoin：用于Monero加密货币，确保交易金额和参与者的隐私。
- Zerocoin：一种加密货币协议，提供匿名交易功能。
零知识证明（Zero-Knowledge Proof）：证明者在不泄露具体信息的情况下，向验证者证明其拥有某个秘密。
累加器（Accumulator）：一种加密结构，允许集合元素的有效证明和验证。
Overview of Advances in Distributed Consensus「分布式共识」
- Distributed Randomness Generation：生成分布式随机数，用于提高系统安全性和公平性。
- Threshold Signature, Publicly-Verifiable Secret-Sharing：
  - 门限签名（Threshold Signature）：需要多个签名者共同签名才能生成有效签名。
  - 公开可验证秘密共享（Publicly-Verifiable Secret-Sharing）：允许公开验证秘密共享的正确性。
- Verifiable Random Function：一种加密函数，生成可验证的随机数，用于提高系统的安全性。

Crypto/Security Perspectives

Mint a coin: finding (partial) collision of a hash function「铸造币：寻找（部分）哈希函数的碰撞」
- 在加密货币中，铸造硬币的过程通常涉及解决一个复杂的计算问题，这个问题的核心是找到一个哈希函数的碰撞。
- 哈希碰撞是指两个不同的输入产生相同的哈希值。在比特币中，这个过程被称为“挖矿”
Transfer a coin: certifying the transaction using signature
Store a coin: record the transaction on “chain of blocks”

Decentralized

from the trust perspective: not centralized -> not trusting any party
better than Chaum’s/traditional cryptographic e-cash under a bank

Secure

尽管加密货币系统提供了较高的安全性，但并不一定完全匿名。
交易记录在区块链上是公开的，尽管用户的身份可以通过加密技术进行隐藏，但仍有可能通过交易模式和其他信息进行追踪和识别。

Cryptography

From Greek: "kryptos" (secret) and "grapho" (writing)
最初，密码学被认为是一种“秘密书写”的艺术
- 即未授权的人无法读取加密后的信息
- 同样地，未授权的人也无法生成密文

Basic Principles/Premises

A goal of "modern cryptography" is to reduce trust
- 传统的安全措施往往依赖于对特定实体或系统的信任
- 而加密技术通过数学和计算理论提供安全保障，无需过多依赖外部信任。
ensuring security despite threats
There're scenarios which you can't ensure security without cryptography.
Cryptography ensures security by assuming "some secret knowledge".
The secret is usually a random key, and must not be the algorithm itself.
Compiled code can be reverse-engineered, tamper with, etc.

Hash Functions

Functionalities

take any string as input
produce fixed-size output (we will use 256 bits)
efficiently computable (but how? or what is inefficient?)

Security properties

collision-free
hiding (or one-way)
puzzle-friendly

Collision Resistance

攻击者无法找到两个不同的输入 x和 y 使得它们的哈希值相同 H(x)=H(y) ，因为计算资源是有限的（计算能力受限）。这意味着找到这样的碰撞需要极高的计算资源，实际操作中是不可行的。

But collisions must exist by definition.
The real question: how much effort is needed to find them?

Birthday Paradox

How possible is it to find a collision

计算所有学生生日都不相同的概率。
第一个学生的生日可以是任意一天，所以概率是365/365。
第二个学生的生日必须与第一个学生不同，所以概率是364/365。
第三个学生的生日必须与前两个学生不同，所以概率是363/365。
依此类推，第23个学生的生日必须与前22个学生不同，所以概率是343/365。
所有学生生日都不相同的总概率是： $( \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \ldots \times \frac{343}{365} )$
计算结果大约为0.4927。
至少有两个人生日相同的概率是：
( 1 - 0.4927 = 0.5073 )

所以在23个学生中，至少有两个人生日相同的概率大约为50.73%。

对于 SHA256 有一种找到碰撞的方法！

假设我们有一个哈希函数，其输出空间有 (N) 种可能的哈希值（对于256位哈希函数， $(N = 2^{256})$ 。我们想要计算在选择 (k) 个随机输入后，至少有两个输入产生相同哈希值的概率。
有k个输入都不发生碰撞的概率为： $P(\text{无碰撞}) = \frac{N}{N} \times \frac{N-1}{N} \times \frac{N-2}{N} \times \cdots \times \frac{N-(k-1)}{N}$
发生碰撞的概率就是1减去不发生碰撞的概率： 1 - P(无碰撞)
对于 (k = 2^130) 和 (N = 2^256) 的情况，可以用近似公式进行计算： $P(\text{无碰撞}) \approx e^{-\frac{k^2}{2N}}$
当 (k = 2^130) 和 (N = 2^256) 时：
$[ \frac{k^2}{2N} = \frac{(2^{130})^2}{2 \times 2^{256}} = \frac{2^{260}}{2 \times 2^{256}} = \frac{2^{260}}{2^{257}} = 2^{3} = 8 ]$
$P(\text{发生碰撞}) \approx 1 - e^{-8} \approx 1 - \frac{1}{e^8} \approx 1 - \frac{1}{2980} \approx 0.9997$

所以尝试2^130个随机选择的输入，有99.8%的概率，其中两个输入会产生相同的哈希值（即发生碰撞）。

但是，找到碰撞所需的时间太长，以至于在实际应用中并不具有现实意义。

对于某些哈希函数H，如果其设计或实现较弱，是有可能找到更快的方法来找到碰撞的。这意味着哈希函数的安全性可能因其具体实现而异。
彩虹表和字典攻击是常见的攻击方法，它们通过预计算和查找来尝试找到哈希值对应的原始输入。

Existing Hash Functions

Best-known cryptographic hash functions: MD5 (128 bits), SHA-1 (160 bits)

MD5: A attack in 2012 breaks collision resistance in 2^18 time.
- This attack runs in less than a second on a desktop computer.
SHA-1: Some theoretical attacks - not yet collisions
虽然目前对 SHA-1 还没有实际的碰撞攻击，但已经存在一些理论上的攻击方法。
~2^63 SHA-1 computations (>10^4 USD per attack)
Use SHA-2 (256 or 512, in Bitcoin)
- SHA-2 有 256 位和 512 位两种版本，并在比特币中使用。
- 或者使用 SHA-3/Keccak（以太坊中使用）
Post-quantum secure? hash-based cryptography 「后量子安全？基于哈希的密码学」

“Tuning” Collision Resistance

如果攻击者成功找到了两个不同的输入 x 和 y 使得 H(x) = H(y)，那么他们一定付出了相当大的计算“努力”，即消耗了大量的计算资源和时间。

如果降低碰撞抗性，那么找到碰撞将变得“可解”，即变得相对容易。这种调整使得哈希函数的碰撞抗性不再是绝对的，而是可以根据需要进行调节。如定义工作量证明的条件，例如哈希值的前四位为零。

Application

Hash as message digest

如果 x 和 y 的哈希值相等，即 H(x) = H(y)，则可以安全地假设 x = y。
To recognize a file that we saw before, just remember its hash.
Useful because the hash is small.
That is why digital signature uses hash function.

Hiding

Hiding property/One-wayness of Hash function ensures: Given H(x), it is infeasible to find x.

Hiding property「隐藏属性」

如果随机数r是从一个具有高最小熵的概率分布中选择的，那么给定H(r || x)（其中r和x是连接在一起的），是无法找到x的。
实际上，找到r || x在计算上是不可行的。这进一步强调了哈希函数的安全性，因为它确保了哈希值不能被逆向破解。

High min-entropy「高最小熵」

高最小熵是指概率分布非常分散，没有一个特定的值具有显著的概率。
没有一个值占据主要的概率，这种分布使得预测某个特定值变得极其困难。
no particular value is chosen with more than negligible probability 「：没有一个特定的值被选择的概率超过可忽略的程度」

假设r是一个128位的随机数，x是一个任意长度的输入。由于r具有高最小熵，其每个可能值的概率为1/2^128，极其小。给定H(r || x)，即使攻击者知道哈希值，也无法在合理时间内找到r || x，从而无法找到x。

Commitment

Want to “seal a value/message in an envelope”, and “open the envelope” later.
Commit to a value, reveal it later.
A sealed letter provides confidentiality「隐私性」 & integrity「完整性」

Example

Alice选择一个随机数r，并计算承诺值C = Hash(123 || r)。
Alice将承诺值C发送给Bob。
Bob收到承诺值C后，无法知道数字123是什么。
当Alice决定揭示数字时，她将123和r发送给Bob。
Bob计算Hash(123 || r)，并验证是否等于C。如果相等，说明数字没有被篡改。

Commitment API

commit 函数可以在内部生成随机数，这些随机数用于生成打开值 opening，类似于加密中的“盐”（salt），增加系统的安全性和不可预测性。即 commit(msg) 产生 com, opening
首先，通过 commit(msg) 生成承诺值 com 和打开值 opening，然后将承诺值 com 发布出去。
发布打开值 opening 和原始消息 msg。
任何人都可以使用 verify() 函数来检查承诺值 com、打开值 opening 和消息 msg 的合法性。此函数返回 true or false

Security properties

Hiding: Given com, infeasible to find msg.
Binding: Infeasible to find msg ≠ msg' such that verify(com, opening', msg') = true

Puzzle-friendly

if k is chosen from a distribution with high min-entropy
then it is infeasible to find x such that H(k || x) = y

给定一个“谜题 ID” id（来自高最小熵分布）。这意味着这个谜题 ID 具有高不确定性和复杂性，使得预测或破解变得困难。

以及一个目标集 Y：尝试找到一个“解” x，使得 H(id || x) 属于 Y。这里，H 是哈希函数，id || x 表示将 id 和 x 连接起来。

将位串视为二进制数。这意味着我们将0和1的字符串解释为二进制数进行处理和操作。
所有数都小于一个固定值。这意味着我们在搜索解 x 时，只考虑小于某个固定值的数。
所有字符串都以一定数量的0开头。这是对解 x 的一个约束条件。
小于某个数 D 的整数集合。这是对目标集 Y 的一个描述，表示我们只考虑小于 D 的整数。
D 越大，谜题就越容易。这是因为目标集 Y 的元素更多，找到符合条件的解 x 的概率更大。

Example

假设我们有一个“谜题 ID” id = 1011，目标集 Y 包含所有小于 16 的整数。我们的目标是找到一个解 x，使得 H(id || x) 属于 Y。

选择一个可能的解 x，例如 x = 001。
连接 id 和 x：id || x = 1011001。
计算哈希值 H(1011001)。
检查 H(1011001) 是否在目标集 Y 中。

假设 H(1011001) = 10，而 10 属于目标集 Y（因为 10 < 16），那么 x = 001 是一个有效的解。

Hashcash, PoW before Bitcoin

Hashcash是一种工作量证明算法。工作量证明（PoW）是一种通过要求计算一定量的工作来防止滥用或滥发请求的方法。
Hashcash被用作多种系统中的拒绝服务攻击对策技术。通过增加发送请求的计算成本，Hashcash有效地减少了恶意请求的数量。
Hashcash戳记构成了一种工作量证明，发送者需要完成一定量的计算工作。这种工作量是可参数化的，即可以根据需要调整计算难度。
接收者（以及任何人，因为它是公开可审计的）可以高效地验证收到的Hashcash戳记。这意味着任何人都可以检查和验证这些戳记的有效性。
Hashcash最广泛的应用是作为比特币挖矿功能。比特币挖矿使用了Hashcash的工作量证明机制，通过解决复杂的数学问题来验证交易并添加到区块链中。

SHA-256 (via Merkle-Damgå rd)

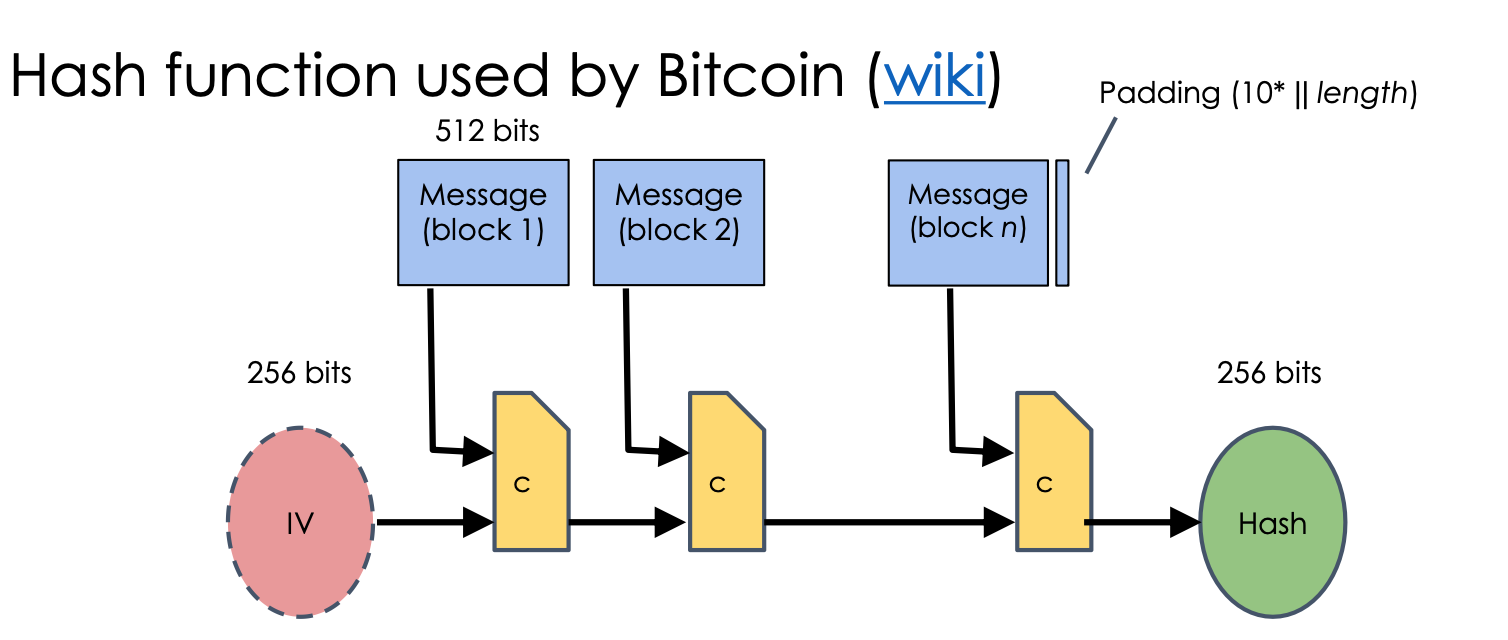
输入数据被分成多个512位的块，每个块被依次处理。图中显示了三个数据块（block 1, block 2, block n），但实际应用中数据块的数量可以更多。
为了确保输入数据的长度是512位的整数倍，SHA-256使用填充技术。填充方法是将一个“1”位和若干个“0”位添加到数据末尾，最后添加数据长度的64位表示。
每个数据块经过处理后生成256位的中间哈希值，这个值将作为下一个数据块处理的初始输入。
IV: 初始向量（IV）是哈希计算的起始状态。在SHA-256中，IV是由标准固定的。
C: 表示压缩函数。每个数据块通过压缩函数处理，与前一个数据块的输出（或初始向量）组合，生成新的中间哈希值。
定理：如果压缩函数C（从768位到256位）是抗碰撞的，那么SHA-256也是抗碰撞的。IV是标准固定的初始哈希值。

Hash Pointers and DS

选择任何基于指针的数据结构。基于指针的数据结构是指其元素之间通过指针连接的结构，如链表、树等。
将指针替换为加密哈希值。

现在我们有了一个经过认证的数据结构。经过认证的数据结构意味着其数据的完整性和真实性得到了保证。

哈希指针指向某些信息存储的位置，而这个位置本身是该信息的一个加密哈希值。
也就是说，哈希指针不仅指向数据的位置，还包含了该数据的哈希值。
- 如果我们有一个哈希指针，我们可以请求获取该信息，并验证其是否未被修改
- 通过比较存储的数据的当前哈希值和哈希指针中存储的哈希值，我们可以确认数据的完整性。

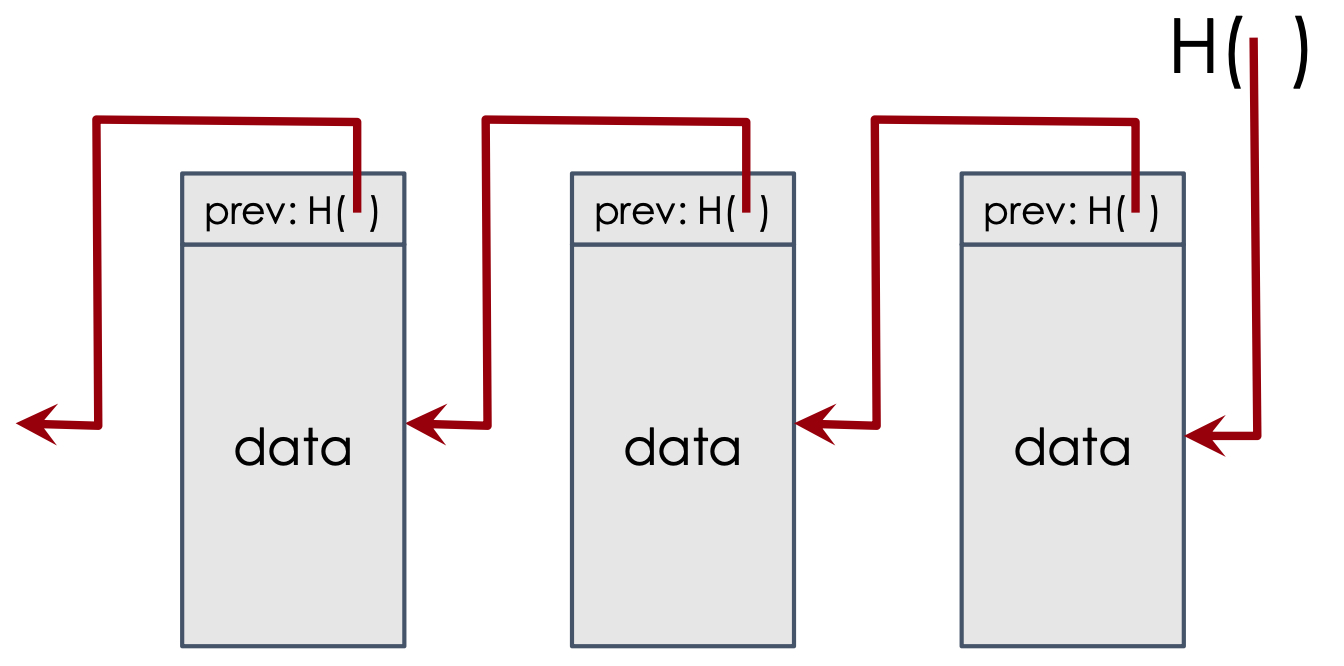
Linked list w/ hash pointers = “block chain”

prev: H( ) 是每个块包含一个指向前一个块的哈希值的指针。这个哈希值是通过对前一个块的数据进行哈希计算得到的。

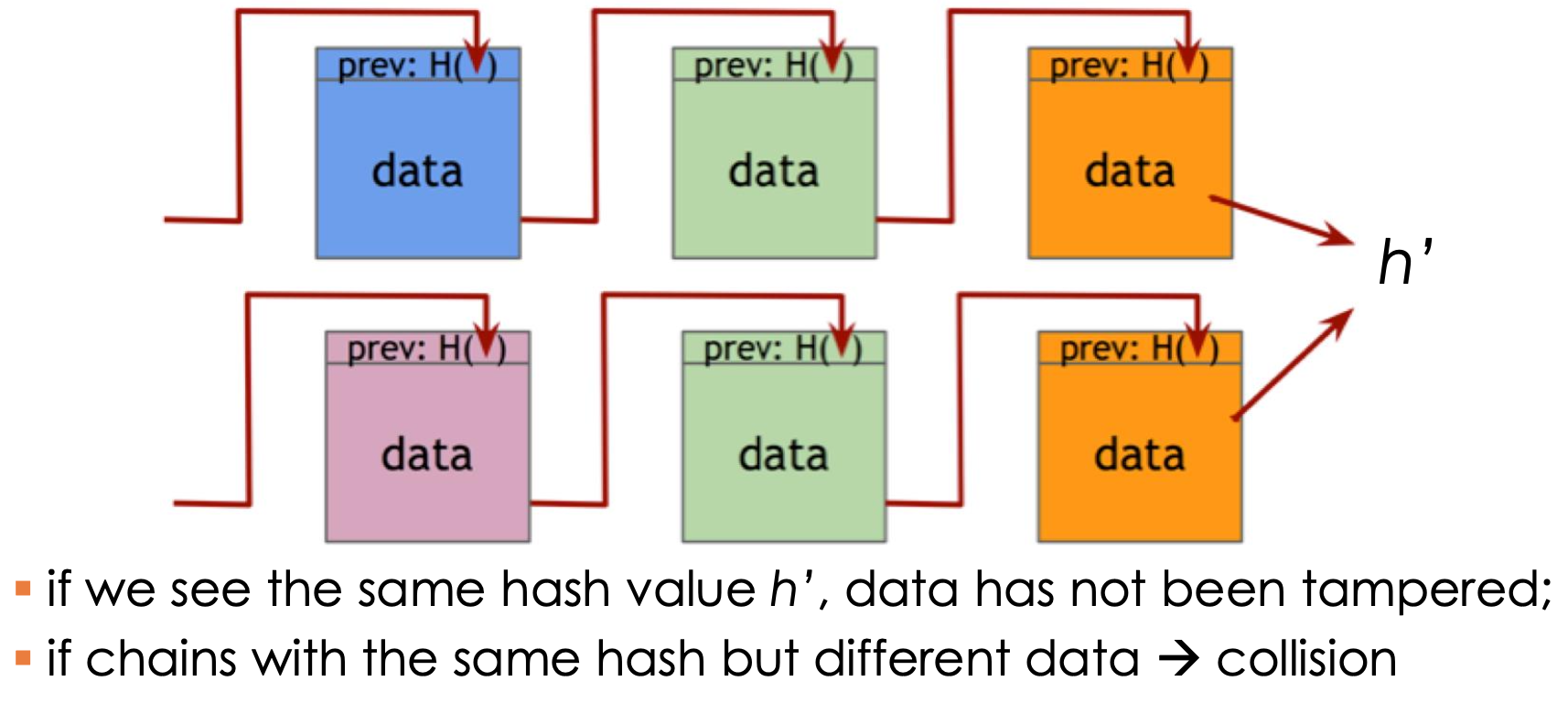
Merkle tree

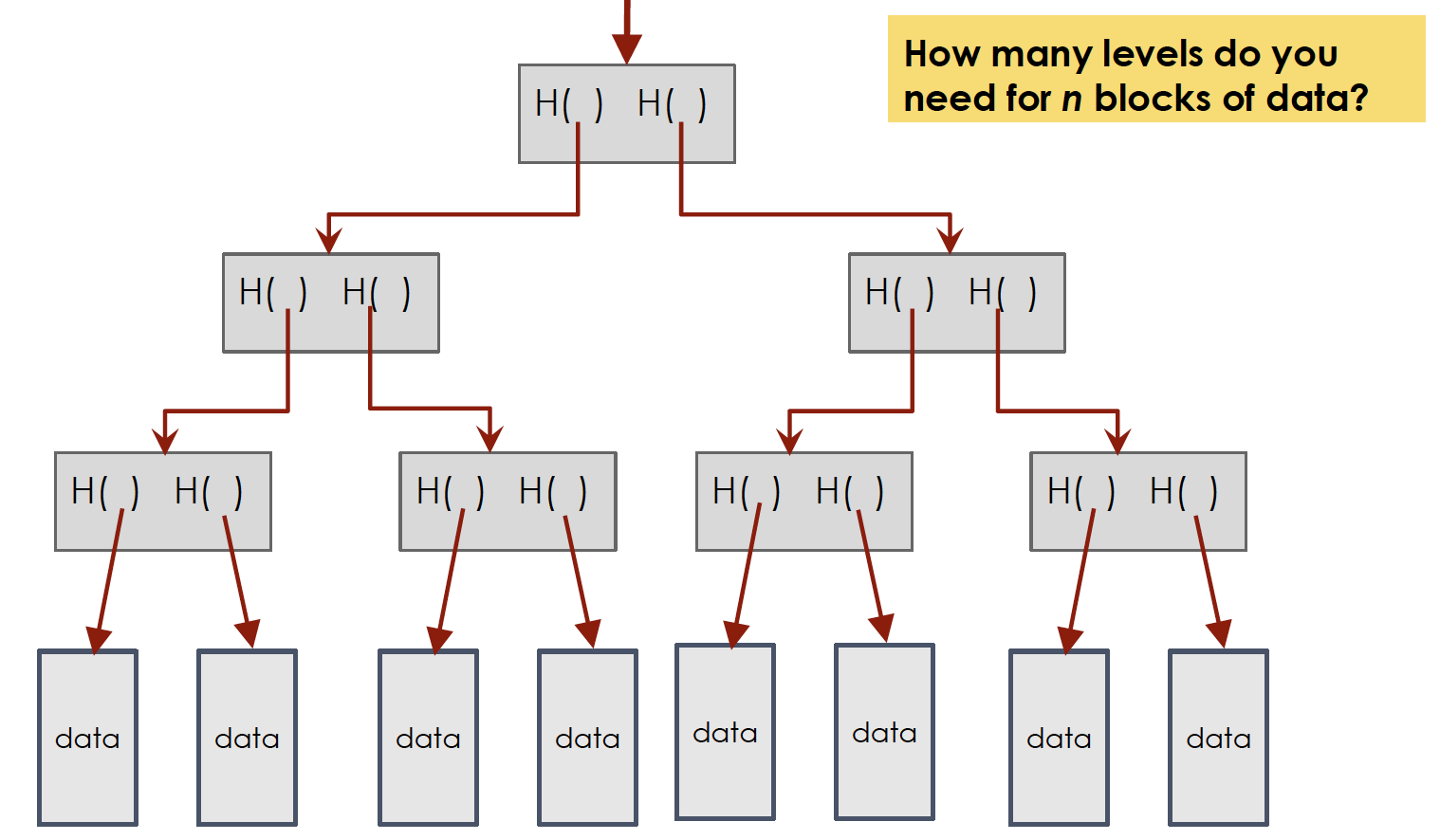
Merkle树是一种带有哈希指针的二叉树

每个叶子节点（最底层的节点）都包含数据块
每个非叶子节点包含其子节点哈希值的哈希值。

具体来说：

最底层的节点是数据块。
上一层的节点是这些数据块哈希值的哈希值。
再上一层是前一层哈希值的哈希值，以此类推，直到根节点。
每个节点的哈希值用H()表示。

假设我们有8个数据块，如何构建Merkle树来验证这些数据块的完整性？

我们需要构建一棵二叉树，其中叶子节点是数据块的哈希值，非叶子节点是其子节点哈希值的哈希值。
计算每个数据块的哈希值，得到8个哈希值。
将相邻的两个哈希值组合，计算其哈希值，得到4个哈希值。
再次组合相邻的哈希值，计算其哈希值，得到2个哈希值。
最后组合这两个哈希值，计算其哈希值，得到根节点的哈希值。

最终，我们得到根节点的哈希值，这个值用于验证整个数据集的完整性。

Membership proof in a Merkle tree: 在Merkle树中进行成员证明时，只需要展示O(log n)个项目。O(log n)表示对数时间复杂度，意味着验证路径的长度与树的高度成对数关系。

Flat Structure

在平面结构中，所有数据项都简单地排列在一个列表或数组中。

要证明某个数据项是否存在于这个列表中，最坏情况下需要遍历整个列表，检查每一个数据项。这种情况下，验证的复杂度是 O(n)，其中 n 是数据项的数量。

Advantages

尽管Merkle树可以存储大量的数据项，但我们只需要记住根哈希值（root hash）即可。
根哈希值是整个树的唯一标识，通过它可以验证整个树的完整性。
Merkle树可以在O(log n)的时间和空间复杂度内验证某个数据项是否存在于树中。
通过比较叶子节点到根节点的路径上的哈希值，可以快速验证数据项的存在性。
排序Merkle树是一种特殊的Merkle树，其中数据项按一定顺序排列。
- 排序Merkle树可以进一步优化数据的验证和查找操作。
- 排序Merkle树还可以在O(log n)的时间复杂度内验证某个数据项是否不存在于树中。
- 在验证某个数据项不存在时，排序Merkle树可以显示缺失数据项之前和之后的项，从而提供更多的上下文信息。
- 提高数据的完整性和安全性。

Comparison

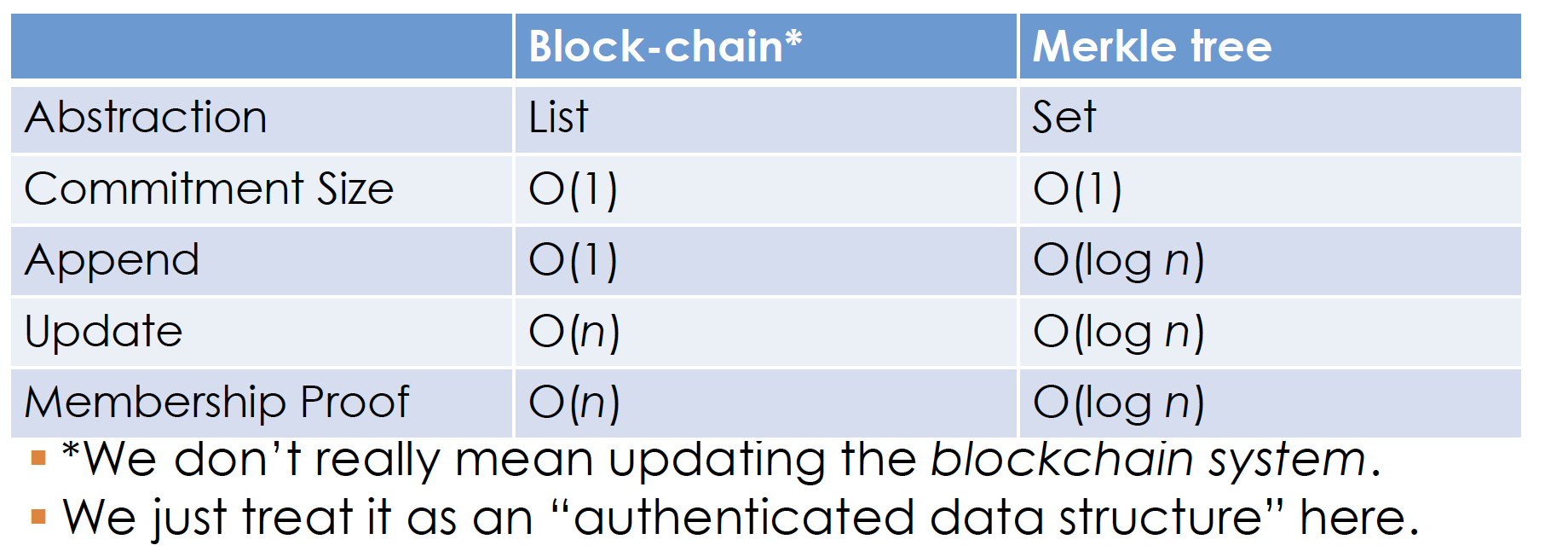
Reclaiming space

通过丢弃“深埋的交易”来回收存储空间。这些交易已经被多个区块确认，因此可以安全地丢弃，而不会影响区块链的整体完整性。

在丢弃交易的过程中，不会影响到Merkle哈希树的结构和指针。Merkle树的根哈希值依然可以用于验证剩余交易的完整性。

A representation of Bitcoin Blockchain

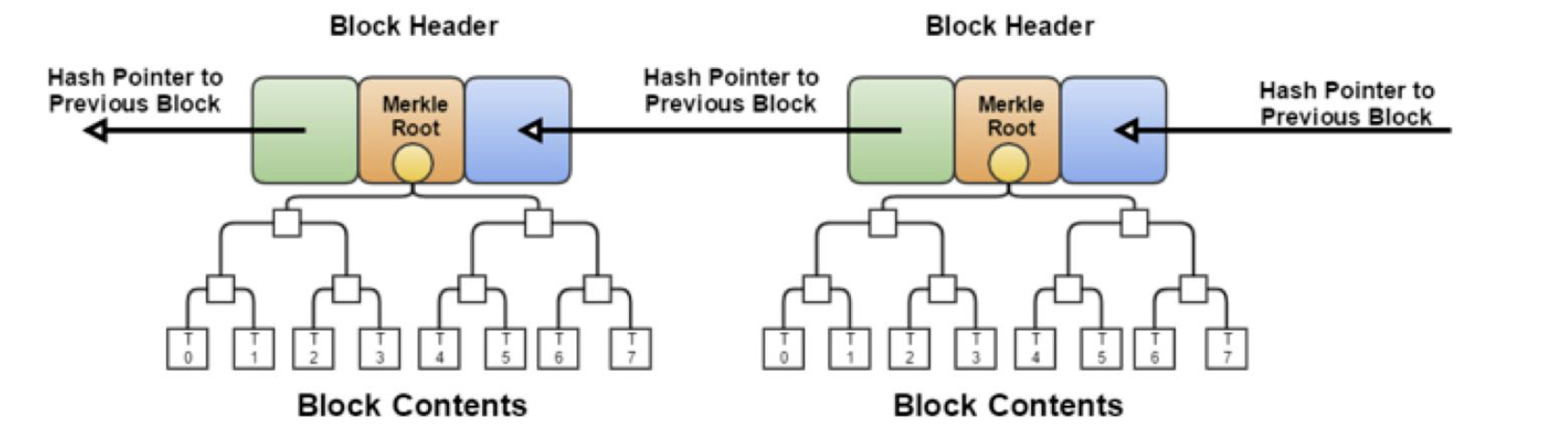
假设你是一名开发者，需要验证某个比特币交易是否被包含在区块链中。

你需要通过查询区块链中的区块来找到包含该交易的区块，并验证该区块的哈希值和梅克尔根。

通过使用梅克尔树和哈希指针，可以快速验证交易是否被包含在区块链中，并确保数据的完整性和不可篡改性。

获取交易的哈希值。
查询区块链中的区块，找到包含该交易的区块。
验证该区块的哈希值是否与前一个区块的哈希值匹配。
使用梅克尔树验证该交易是否包含在区块中。
确认该区块的梅克尔根与区块头中的梅克尔根一致。

Digital Signatures & Public-Key Encryption

Workflow of Digital Signature

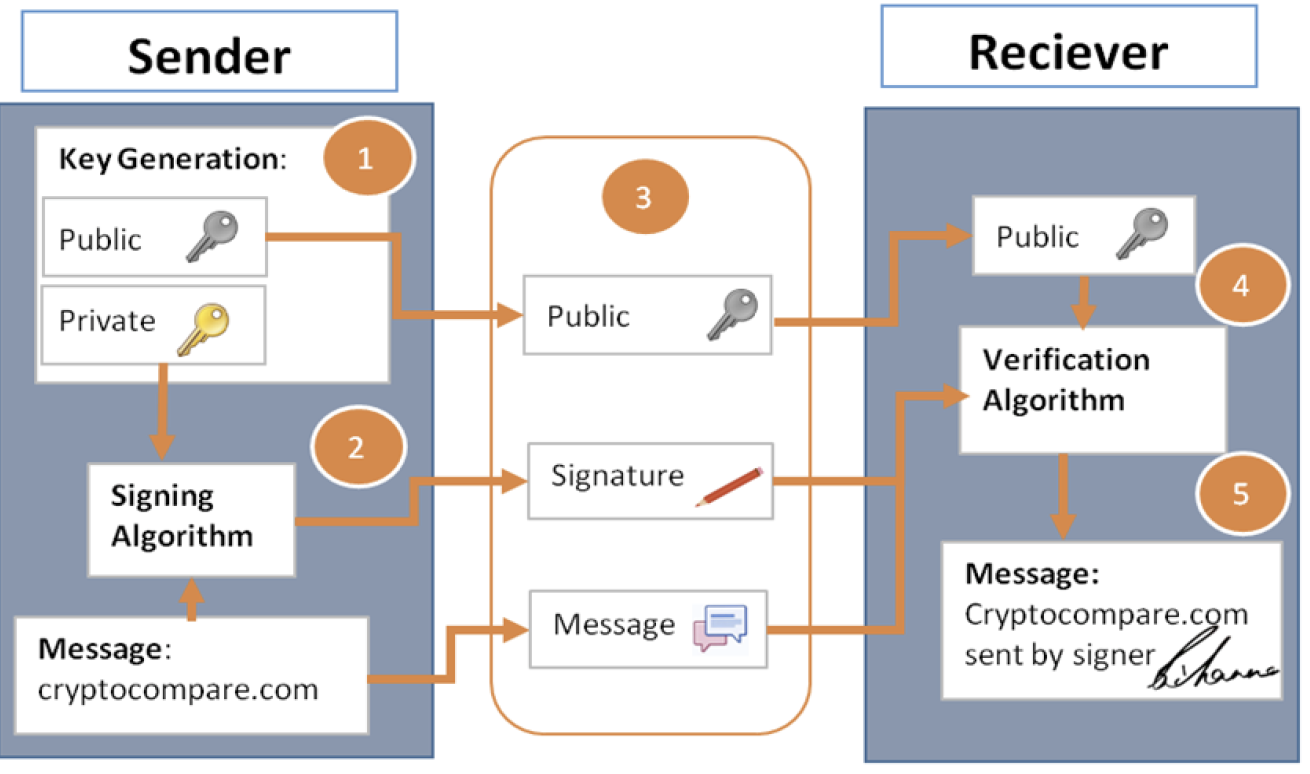
One-time security vs. Multi-time security

一次性签名是一种只使用一次的签名方法，通常用于非常高安全性要求的场景。
- 它的主要优点是，即使签名私钥被泄露，也不会影响其他消息的安全性。
- 一次性签名使用一次性的私钥和公钥对来签名和验证消息。每个私钥和公钥对只能使用一次，之后就会被废弃。
多次签名允许同一个签名密钥对多次使用，适用于需要频繁签名的场景
- 尽管方便，但如果私钥被泄露，所有使用该私钥签名的消息都可能被伪造。
- 多次签名使用相同的私钥来签名多次消息，接收者使用相同的公钥来验证这些签名。

ECDSA

Elliptic Curve Digital Signature Algorithm「椭圆曲线数字签名算法」

ECDSA算法依赖于随机数生成器来生成签名的随机部分。如果随机数生成器不够好，生成的随机数可能会被预测，从而导致签名被破解。
如果在不同的签名中重复使用相同的随机数，会导致严重的安全问题。攻击者可以利用这些重复的随机数来推断出私钥，从而伪造签名。
重复使用随机数会泄露私钥（sk）。攻击者可以通过分析不同签名中的相同随机数来计算出私钥。
理论上，避免重复使用随机数可以防止这种攻击，但在实际操作中，人们可能会犯错误，导致随机数被重复使用。

ECDSA并不是“强不可伪造”的。攻击者可以利用某些弱点来伪造签名。

给定一个消息（m）和其签名（sig），攻击者可以创建一个新的有效签名（sig'）。这被称为交易可塑性（tx malleability）问题。
ECDSA不具备抗量子计算的能力。量子计算机可以使用Shor算法快速破解ECDSA。
ECDSA不容易扩展到阈值签名「threshold case」的情况。

Why: avoid “single point of failure” in terms of security

lost one secret, everything lost! e.g., your bitcoin
Idea: split secret into N pieces, such that given any t pieces, can reconstruct the secret
given fewer than t pieces, don’t learn anything

Example

假设你有一个秘密数字S=12345，你希望将其分成两个部分X1和X2，使得只有拥有这两个部分的人才能重建这个秘密。

你需要选择一个大素数P和一个随机数R。
通过将S加上R和2R，然后取模运算生成X1和X2。

这个问题使用秘密分享的知识点，因为你希望确保只有拥有所有部分的人才能重建秘密，而单独一个部分无法泄露任何信息。

选择一个大素数P，例如P=100003（为了简单起见）。
选择一个随机数R，例如R=67890。
计算X1 = (S + R) mod P = (12345 + 67890) mod 100003 = 80235。
计算X2 = (S + 2R) mod P = (12345 + 2*67890) mod 100003 = 148125 mod 100003 = 48122。

现在你有两个部分X1=80235和X2=48122。

要重建秘密：

计算(2X1 - X2) mod P = (2*80235 - 48122) mod 100003 = 160470 - 48122 = 112348 mod 100003 = 12345。

这样，你成功重建了秘密S=12345。

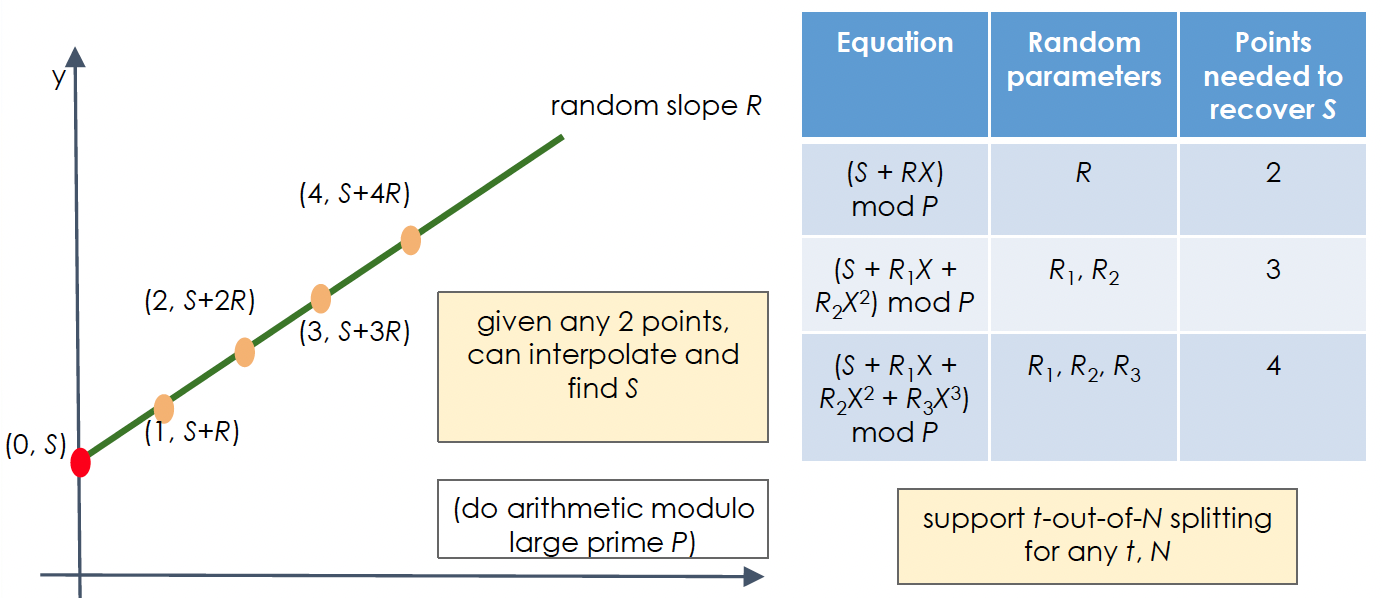
这张图显示了秘密分享的基本概念。

图中的点代表了秘密分享方案中的各个份额。
每个点的形式为 (x, y)，其中 x 是一个索引，y 是通过一个多项式计算得到的值。

关键概念

随机斜率 R: 这是一个随机生成的参数，用于确保每个份额的唯一性和安全性。
插值和恢复 S: 通过给定的两个或更多点，可以使用多项式插值法来重构秘密 S。
模运算 P: 所有计算都在模数 P 下进行，以确保结果在一个固定范围内。

给定任意 2 个点，可以插值并找到 S

Example

假设我们有一个秘密 S = 123，我们选择一个大素数 P = 7919，并且我们希望将秘密分成5个份额，但需要至少3个份额才能恢复秘密。

我们选择一个二次多项式 (S + R₁ X + R₂ X^2) mod P，其中 R₁= 456 和 R₂ = 789。

(1, (123 + 456*1 + 789*1^2) mod 7919)
(2, (123 + 456*2 + 789*2^2) mod 7919)
(3, (123 + 456*3 + 789*3^2) mod 7919)
(4, (123 + 456*4 + 789*4^2) mod 7919)
(5, (123 + 456*5 + 789*5^2) mod 7919)

计算份额：

(1, 1368)
(2, 3705)
(3, 7452)
(4, 2609)
(5, 916)

我们有5个份额，但需要至少3个份额来重构秘密。假设我们有份额 (1, 1368)、(2, 3705) 和 (3, 7452)，我们可以使用拉格朗日插值法来重构秘密 S = 123。

要使用拉格朗日插值法重构秘密 ( S = 123 ) ，我们需要使用三个份额 ((1, 1368))、((2, 3705)) 和 ((3, 7452))。我们将使用这些点来构造一个二次多项式，并找到其常数项（即秘密 ( S )）。

拉格朗日插值法的公式如下：

f(x) = \sum_{j=0}^{k-1} y_j \prod_{\substack{0 \le m < k \\ m \neq j}} \frac{x - x_m}{x_j - x_m}

其中 ( (x_j, y_j) ) 是已知点， ( k ) 是点的数量。在我们的例子中， ( k = 3 )。

首先，我们计算拉格朗日基函数 ( L_j(x) )：

L_0(x) = \frac{(x - x_1)(x - x_2)}{(x_0 - x_1)(x_0 - x_2)}

L_1(x) = \frac{(x - x_0)(x - x_2)}{(x_1 - x_0)(x_1 - x_2)}

L_2(x) = \frac{(x - x_0)(x - x_1)}{(x_2 - x_0)(x_2 - x_1)}

我们将 ( x ) 设为 0，因为我们需要找到多项式的常数项。

计算 ( L_0(0) )：

L_0(0) = \frac{(0 - 2)(0 - 3)}{(1 - 2)(1 - 3)} = \frac{(-2)(-3)}{(-1)(-2)} = \frac{6}{2} = 3

计算 ( L_1(0) )：

L_1(0) = \frac{(0 - 1)(0 - 3)}{(2 - 1)(2 - 3)} = \frac{(-1)(-3)}{(1)(-1)} = \frac{3}{-1} = -3

计算 ( L_2(0) )：

L_2(0) = \frac{(0 - 1)(0 - 2)}{(3 - 1)(3 - 2)} = \frac{(-1)(-2)}{(2)(1)} = \frac{2}{2} = 1

然后，我们将这些值代入拉格朗日插值公式：

f(0) = y_0 L_0(0) + y_1 L_1(0) + y_2 L_2(0)

代入已知的 ( y ) 值：

f(0) = 1368 \cdot 3 + 3705 \cdot (-3) + 7452 \cdot 1

进行计算：

f(0) = 1368 \cdot 3 = 4104

f(0) = 3705 \cdot (-3) = -11115

f(0) = 7452 \cdot 1 = 7452

将这些结果相加：

f(0) = 4104 - 11115 + 7452

进行最终计算：

f(0) = 4104 + 7452 - 11115 = 123

因此，我们成功地重构了秘密 ( S = 123 )。

Good & Bad

Good:
- Store shares separately
- adversary must compromise several shares to get the key
Bad
- To sign, need to bring shares together to reconstruct the key ⇔ vulnerable「易受攻击」

Application

"Threshold signing"「门限签名」: Sign with the share separately

“门限签名”是一种技术，允许使用各个部分分别进行签名，而无需重构完整的密钥。这样可以避免在签名过程中暴露完整的密钥。

门限签名技术的核心思想是重构签名而不是重构密钥。这样，即使签名过程中某个部分被泄露，也无法获取完整的密钥。
门限签名需要一个兼容且安全的方案来实现。这意味着需要特定的算法和协议来确保门限签名的安全性和有效性。
并不是所有的加密方案都可以扩展到门限签名的应用场景。因此，在选择加密方案时，需要确保其支持门限签名。

Managing Secret Keys

用户可以拥有多个公钥和私钥对。每个公钥和私钥对通常对应一个特定的加密货币地址，例如比特币地址或以太坊地址。
每个比特币地址或以太坊地址都有一个唯一的公钥和私钥对。这意味着用户可以为每个加密货币地址生成一个新的公钥和私钥对，以提高安全性。
钱包是用于管理公钥和私钥的工具。它们可以生成新的公钥和私钥对，并安全地存储私钥。
钱包生成公钥和私钥对，并安全地存储私钥。公钥可以公开分享，而私钥必须保密。
钱包可以发布和验证交易。发布交易是指将加密货币从一个地址发送到另一个地址，而验证交易是确保交易的合法性和有效性。
钱包可以显示用户的余额，即用户在各个加密货币地址上的总资产。

Types of Wallets

cloud：secret keys on a cloud... like a bank (e.g., Coinbase).
laptop/phone：Electrum, MetaMask, ...
hardware：Trezor, Ledger, Keystone, ...
paper：print all sk on paper
brain：memorize sk (bad idea)
Hybrid：non-custodial cloud wallet (threshold sig.)

Simplified Payment Verification (SPV)

客户端钱包如何显示Alice的当前余额？这涉及到钱包如何验证和更新用户的交易数据，以显示最新的余额。
笔记本电脑或手机钱包需要验证一笔即将到来的支付。
为了确保支付的有效性，钱包需要验证交易是否已被区块链网络确认。
目标：在不下载整个区块链（366 GB）的情况下完成此操作。
区块链数据非常庞大，下载和存储整个区块链对普通设备来说是不现实的，因此需要一种更轻量的方法。
1. 下载所有区块头（60 MB）。区块头包含了验证交易所需的基本信息，但数据量相对较小。
2. 下载相关的交易（Tx’s）。只下载与钱包地址相关的交易数据，而不是所有交易数据。
钱包 → 服务器：我的钱包地址列表。钱包将用户的地址列表发送给服务器，以请求相关交易数据。
服务器 → 钱包：涉及地址的交易数据。服务器返回与这些地址相关的交易数据。
Merkle树（成员）证明相对于区块头。使用Merkle树结构验证交易数据的完整性和有效性。

Hardware Wallet

On Ledger

在初始化账本时，用户需要进行一系列的设置和配置，以确保钱包的安全性。这包括生成和备份助记词、设置PIN码等步骤。
用户会被要求写下24个助记词。这些词语是钱包生成的，用于备份和恢复钱包。用户必须妥善保存这些词语，因为它们是访问钱包和资金的唯一途径。
每个词语编码11位二进制信息。24个词语一共编码了268位信息。这些信息用于生成钱包的种子，从而生成私钥和公钥。
BIP 39定义了一个包含2048个词语的词库，这些词语可以用多种语言表示。用户在初始化钱包时，设备会从这个词库中随机选择24个词语。
要警惕“预初始化的硬件钱包”（例如，从eBay购买）。这些钱包可能已经被恶意初始化，助记词可能已经被记录下来，导致资金被盗的风险。
2018年，有用户购买了预初始化的硬件钱包，资金转入钱包后立即被盗。这是因为这些钱包的助记词已经被攻击者记录下来，导致资金被转移。

Crypto Toolbox

# Crypto Toolbox

# Topics

# Crypto/Security Perspectives

# Decentralized

# Secure

# Cryptography

# Basic Principles/Premises

# Hash Functions

# Collision Resistance

# Birthday Paradox

# Existing Hash Functions

# “Tuning” Collision Resistance

# Application

# Hiding

# Commitment

# Puzzle-friendly

# Hashcash, PoW before Bitcoin

# SHA-256 (via Merkle-Damgå rd)

# Hash Pointers and DS

# Merkle tree

# Advantages

# Comparison

# Reclaiming space

# A representation of Bitcoin Blockchain

# Digital Signatures & Public-Key Encryption

# Workflow of Digital Signature

# One-time security vs. Multi-time security

# ECDSA

# Secret sharing

# Example

# Secret sharing depicted

# Good & Bad

# Application

# Managing Secret Keys

# Types of Wallets

# Simplified Payment Verification (SPV)

# Hardware Wallet

# On Ledger

Crypto Toolbox

Topics

Crypto/Security Perspectives

Decentralized

Secure

Cryptography

Basic Principles/Premises

Hash Functions

Collision Resistance

Birthday Paradox

Existing Hash Functions

“Tuning” Collision Resistance

Application

Hiding

Commitment

Puzzle-friendly

Hashcash, PoW before Bitcoin

SHA-256 (via Merkle-Damgå rd)

Hash Pointers and DS

Merkle tree

Advantages

Comparison

Reclaiming space

A representation of Bitcoin Blockchain

Digital Signatures & Public-Key Encryption

Workflow of Digital Signature

One-time security vs. Multi-time security

ECDSA

Secret sharing

Example

Secret sharing depicted

Good & Bad

Application

Managing Secret Keys

Types of Wallets

Simplified Payment Verification (SPV)

Hardware Wallet

On Ledger