Privacy Enhancing Crypto

How signature is used in blockchain

• 核心思想：公钥 = 身份
• 如果你看到签名sig，使得Verify(pk, msg, sig) = true，可以理解为公钥pk在说，“[消息]”
• UTXO model in Bitcoin, Account model in Ethereum 都使用了 signature

How to make a new identity

• Create a new, random key-pair (sk, pk)
• pk (or the address Hash(pk)) is the public "name" you can use
• You control the identity, because only you know sk
• 无需许可「Permissionless」：任何人可以在任何时间创建一个新的身份。这个过程不需要中央机构的批准或参与。
• Make as many as you want! No central coordination!
• pk "looks random" and not directly connect to real-world identity?!
• 发送者可以为接收者“创建”一个公钥，以实现接收者的匿名性，例如在Monero中（Monero使用UTXO模型). 这种方法可以隐藏接收者的真实身份。

Pseudonymous

「假名」

1730296253162.png

• 在区块链系统中，交易是公开的，因此需要额外的技术手段来保护用户的隐私。
• 比特币交易是公开的，但参与者的身份是隐藏的，只有他们的比特币地址是可见的。
• 这种假名性意味着虽然地址不直接显示用户的真实身份，但通过分析交易记录，仍然可以推断出用户的行为和身份。
• 公钥地址是由公钥生成的字符串，用于接收比特币。它类似于银行账号，可以公开分享。
• 一旦比特币地址与某个人的真实身份关联起来，所有通过该地址进行的交易记录都可以追溯到这个人，从而揭示其财务活动和行为。

Anonymity

or precisely, unlinkability「或者准确地说，不可链接性」

对手银行无法将一笔取款交易与一笔存款交易关联起来。这意味着在电子现金系统中，用户可以从银行取款，然后在不透露身份的情况下将其花费在商家处，而银行无法追踪这些交易。

1. Alice从银行账户中取出100单位的电子现金。
2. 电子现金系统通过加密技术生成一个匿名的电子现金凭证，Alice可以用这个凭证进行支付。
3. Alice在Bob处消费100单位的电子现金，Bob接收到电子现金凭证。
4. Bob将电子现金凭证存入他的银行账户，银行验证凭证的合法性，但无法追踪到Alice。

Fungibility

「可替代性」

• 个体单位可以互相替代：这意味着一个单位的资产可以用另一个相同单位的资产替代，而不会影响其价值
• 比特币可能与你相关，或者被污染「tainted」。
  • 比特币的交易记录是公开的，因此每个比特币的历史可以被追踪到。
  • 如果某个比特币曾经用于非法活动，它可能会被认为是“污染的”。
• 由于比特币的交易记录是公开的，但不一定每个人都会去查看，因此你可能在持有比特币时并不知道它的历史，直到你尝试交换或出售它时才发现。

Transparency of Blockchain

「透明性」

• 区块链的透明性可以提高系统的可信度和安全性。
• 透明性对于敏感信息来说是不理想的「desirable」。
  • 金融交易中的敏感信息如果被公开，可能会导致隐私泄露和安全风险。
  • 例如，两家银行之间的交易细节不应被其他银行知道。

3 Types of Privacy

3 Types of Privacy, 3 Cryptocurrencies with Privacy

Zcash (#20, S&P '14)

• Use ZK-SNARK：Zcash 使用 ZK-SNARK 技术来实现交易的零知识证明，从而确保交易的隐私性。
• Zcash 的零知识证明技术可以扩展到零知识智能合约，使得智能合约的执行过程也能保持隐私。
• K-SNARK 的证明时间大约为 30 秒。
• ZK-SNARK 目前需要一个可信的初始化设置，但未来可以通过技术升级来消除这一需求。

Monero (#13)

• 门罗币通过可链接环签名技术实现发送方的匿名性。
• 通过 Diffie-Hellman 密钥交换实现接收方的匿名性。
• 使用离散对数承诺方案来保证交易内容的隐私。隐私保护技术在实际应用中非常实用。
• 匿名性在扩展性方面存在问题，隐藏发送方的计算复杂度为 O(n)。

Dash (#15)

• 达世币基于 CoinJoin 技术，通过将多个交易的输入和输出混合在一起实现匿名性。
• 达世币使用同态加密「homomorphic」技术将多个交易的输入和输出混合在一起。
• 达世币的匿名性有限，可能无法完全隐藏交易各方的身份。

Privacy Concerns in Signatures

What can we do “with” signatures?

• 一个人可以在一条消息上签名。
• 任何人都可以验证一个签名（基于消息和身份）。
• (Accountable「可追责的」) Signer (Identity) Privacy

Blind Signature

A Simple E-Cash System

你希望在使用电子现金时保持匿名，不让别人知道你具体的消费记录。银行的要求是：他们不希望你进行双重花费。

• 你存入100美元，银行会给你100个1美元的电子硬币。
• 这个过程类似于在银行存款，但你得到的是电子形式的货币。
• 你以签名的形式提取一个单位（1美元）的硬币。这里的签名指的是数字签名，它代表了你对这1美元的所有权。
• 以每个硬币都有一个序列号。这个序列号用于追踪每个电子硬币的使用情况。
• 当你“花费”一个签名时，商家和后来银行会知道这个序列号。
  这个过程确保了每次交易的合法性和可追溯性。但也泄露了你发消费记录。
• 当商家或银行看到相同的序列号时，说明有人进行了双重花费。
• 但由于盲签名技术，提取和消费之间没有关联。
  • 提取阶段：用户从银行提取电子现金时，用户生成一个随机数并将其与电子现金的标识信息结合，形成一个遮蔽后的消息。银行对这个遮蔽后的消息进行签名，而不知原始消息内容。
  • 用户在商家处使用电子现金时，用户解除遮蔽，向商家展示电子现金的原始标识信息和银行的签名。商家可以验证银行的签名但无法知道用户的身份或提取过程。

这是传统加密电子现金的起点（ZeroCash使用了一些类似的概念）。ZeroCash是一种基于零知识证明的电子现金系统，进一步增强了隐私保护。

Functionalities

• 你，作为签名请求者，希望获得一个签名。
• 但是你不希望签名者知道被签名的内容。
• KeyGen()是密钥生成函数，它生成一对公钥和私钥，用于加密和签名。
• 签名变成一个协议或一组算法。签名过程包括多个步骤，确保在保持隐私的情况下完成签名。
• Blind(pk, m) -> (m', r)。
  盲化过程使用公钥(pk)和消息(m)生成盲化消息(m')和盲化因子(r)。
• Blind-Sign(sk, m') -> S'
  盲签名过程使用私钥(sk)对盲化消息(m')进行签名，生成盲签名(S')。
• Unblind(pk, S', r) -> S
  去盲化过程使用公钥(pk)、盲签名(S')和盲化因子(r)恢复原始签名(S)。
• 验证函数Verify()使用公钥(pk)和消息(m)验证签名(S)的真实性。

Generic Scheme

• RSA Signatures and RSA Blind Signatures
• A BLS-based Blind Signatures

A “Generic” Blind Signature Scheme

Blind(pk, m) -> (m', r)

• 在盲签名过程中，首先需要对消息 m 进行盲化处理，这个过程称为 Blind。
• 这里的 pk 是公钥，m 是需要签名的消息。
• 盲化过程生成了一个新的消息 m'，它是 m 的承诺，同时生成一个随机值 r 作为打开值。
• 这个过程确保了签名者看不到原始消息 m。

Blind-Sign(sk, m') -> S'

• 在这个步骤中，签名者使用其私钥 sk 对盲化后的消息 m' 进行签名，生成签名 S'。
• 由于 m' 是盲化后的消息，签名者无法得知原始消息 m 的内容。
• 这个步骤确保了消息的隐私性，同时生成了一个有效的签名。

Unblind(pk, S', r) -> S

• 在这个步骤中，请求者使用打开值 r 和公钥 pk 对签名 S' 进行去盲化，恢复出对原始消息 m 的签名 S。
• 这个过程验证了签名的有效性。

然而，这种方法存在问题，因为签名者可以看到 S' 中的 m'，从而可能将其与原始消息 m 联系起来。

这种联系的原因可能包括以下几点：

1. 消息的唯一性：如果消息 m 是唯一的或具有明显特征，即使经过盲化，签名者也可能通过分析盲化后的消息 m′ 推测出原始消息 m。
2. 盲化因子的可逆性：盲化因子 r 用于将原始消息 m 盲化为 m′。如果盲化因子 r 的选择不够随机或不够强大，签名者可能通过数学分析或反向工程推导出盲化因子，从而推测出原始消息。

Some Discussions

• 盲签名技术作为一种基本的隐私保护技术，在更复杂的加密协议中通常作为入门或基础技术进行介绍和应用。
• 通过对BLS签名算法进行改进，可以实现盲签名协议，从而在签名过程中保护消息的隐私。
• 由此产生的简单电子现金系统仍然是传统的，不基于区块链，也不是去中心化的。
• 尽管盲签名技术在传统电子现金系统中使用，但它也在去中心化的加密货币系统中得到了应用，增强了隐私和安全性。
• 盲签名技术确保了电子货币的不可追踪性，使得无法将多次交易与同一次提现操作关联起来。
• 尽管盲签名技术保护了交易隐私，但发行银行的信息仍然是公开的，如何进一步隐藏这一信息是一个挑战。
• 在加密货币系统中，签名者的角色相当于传统系统中的付款者，负责验证和确认交易。

Ring Confidential Transactions

从签名中隐藏签名者的身份

• 签名的主要目的是验证消息的真实性和完整性。
  • 如果我们不知道签名者是谁，那么签名就失去了验证的意义
  • 因为我们无法确认消息的来源。
• 这进一步强调了签名者身份的重要性。
• 在某些情况下，知道签名来自一组人中的某一个就足够了。例如，在举报或泄密的场景中，保护举报者的身份非常重要。

环签名是一种允许签名者在一组用户中生成签名，同时保持匿名的技术。它有两个主要特性：自发性和匿名性。

• 自发性：签名者可以征召任何一组n个用户。
  • 签名者可以选择任何一组用户来生成环签名，这些用户甚至可能不知道自己被选中。
• 匿名性：验证者无法确定谁是真正的签名者。
  • 验证者只能确认签名来自这组用户中的某一个，但无法确定具体是谁。
  • 这种匿名性通常是无条件的，即使在强大的计算能力下也无法破解。

环签名允许一个用户代表一组可能的签名者签署交易，而不透露实际发起交易的成员是谁。这种机制确保了签名者在群体中的匿名性。

为什么群体中的其他人会愿意帮助真正的签名者？这个问题通过"自发性"（spontaneity）来解决，即群体中的成员不需要事先同意或合作就可以生成环签名。

匿名性意味着没有人知道哪个公钥被"使用"了。环签名技术通过混淆不同成员的公钥来实现这一点，从而隐藏了具体的签名者。

双花？

不断“使用”相同的公钥进行双重支付？

这个问题通过“可链接性”来解决「linkability」。环签名中引入了一个机制，可以检测到重复使用相同公钥的行为，从而防止双重支付。

Signature

• 环签名（1-out-of-n签名）
• 环签名具有以下两个特性
  • 匿名性「Anonymity」：验证者无法确定真实的签名者是谁。通常是无条件的！（相对于计算匿名性）
  • 自发性「Spontaneity」：签名者可以征召任何n个用户组。
  • 这个组甚至可能不知道他们已经“加入”。

Example

假设有一个公司内部举报系统，员工可以匿名举报不当行为。公司希望确保举报信息的真实性，但又不希望知道举报者的身份。

环签名可以确保举报信息的真实性（只有公司内部员工才能签名），同时保护举报者的匿名性（公司无法确定具体的举报者）。

1. 公司内部每个员工都有一对公钥和私钥。
2. 员工A发现了不当行为，决定举报。
3. 员工A使用自己的私钥和其他n-1个员工的公钥生成一个环签名。
4. 公司收到举报信息和环签名后，使用所有员工的公钥验证签名的有效性。
5. 验证通过，公司确认举报信息来自内部员工，但无法确定具体是谁。

Syntax

• KeyGen() 在输入和输出方面保持不变。即，密钥生成过程不变，每个潜在的签名者都可以独立运行它。
• Sign() 应该接收 n 个公钥作为额外输入。
• RingSign({pk_i}i ∈ {1,n}, sk_j ∈ {1,n}, m) -> S
  • RingSign() 函数接收 n 个公钥 {pk_i}、一个私钥 sk_j 和消息 m，生成签名 S。
  • 只需要一个秘密签名密钥，不像多重签名那样需要多个秘密签名密钥。
• Verify() 接收 n 个公钥而不是单个公钥。
• 验证函数 Verify() 需要所有潜在签名者的公钥来验证签名是否有效。即，Verify({pk_i}, m, S) -> True/False。

Example

1. 密钥生成：
   • Alice 生成 (pk_Alice, sk_Alice)。
   • Bob 生成 (pk_Bob, sk_Bob)。
   • Charlie 生成 (pk_Charlie, sk_Charlie)。
2. 签名生成：Alice 使用 RingSign({pk_Alice, pk_Bob, pk_Charlie}, sk_Alice, m) 生成签名 S。
3. 签名验证：验证者使用 Verify({pk_Alice, pk_Bob, pk_Charlie}, m, S) 验证签名是否有效。

Linkable Ring Signature

在密码学中，"可链接性"是一种特性，它允许我们确定两个或更多的签名是否由同一个签名者生成。

可链接环签名是一种改进的环签名方案，增加了签名的可链接性，使得可以检测到重复签名行为。

无条件的匿名性可能被滥用。这意味着完全匿名的签名者可能会利用匿名性进行恶意操作，如双重签名。

Malicious Bob could double-sign!

• 当支付者（账户）是匿名时，如何识别双重支付？
• 这是环签名中的一个关键问题，因为匿名性使得追踪重复签名变得困难。

1730446684400.png

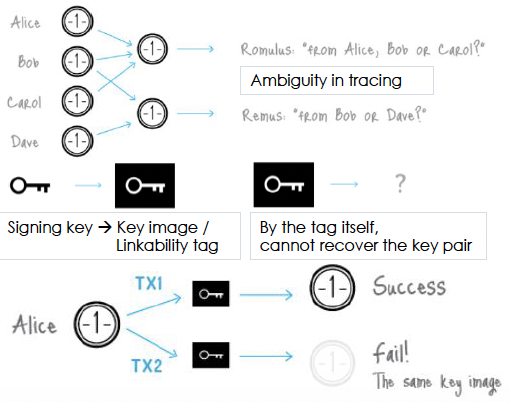
因此，我们在环签名中添加了以下功能

• 我们强制签名者生成一个“密钥图像「key image」”（或“可链接标签「linkability tag」”）。
• 这个密钥图像是签名者的唯一标识符。
• "One-way information" of the key, 这意味着从密钥图像无法反推出签名密钥。
• Same key -> Same tag, 这使得可以检测到重复签名。

FAQ

为什么使用环签名对交易进行签名？

环签名允许一个组中的任意成员代表组进行签名，而不暴露具体是谁签名的。这样，外部观察者无法确定交易的发起者是谁，从而保护了交易发起者的隐私。

例如，在加密货币系统（如Monero）中，环签名被用来混淆交易的输入，使得观察者无法追踪到具体的资金来源。

为什么需要密钥图像？ 直接对比签名是否出现过，不就行了吗？

如果我们只是简单地比较签名是否出现过，那么用户可以用同一私钥和不同的公钥环生成不同的签名，这样就可以多次使用同一笔资金，因为每个签名看起来都是全新的。

密钥图像是由用户的私钥生成的，对于每个私钥，其密钥图像是唯一的。当用户生成一个环签名时，他们也会生成一个密钥图像，并将其包含在签名中。然后，网络会检查这个密钥图像是否已经用过。

密钥图像的设计是为了解决这些问题。它是由用户的私钥生成的，但是它的生成过程包含了一些额外的步骤，以确保它既不能从私钥中直接计算出来，也不会对每个交易产生相同的输出。

• LinkRingSign({pk_i}, sk_j, m) -> S = (S\*, t)
  • LinkRingSign 是一个函数，接受公钥集合{pk_i}，私钥sk_j，以及消息m，输出签名S
  • 其中S包含签名S*和标记t。
  • t是关键图像，可以视为由私钥sk_j唯一确定的标记。这个标记用于确保签名的可链接性。
  • 为了确保t的构造是正确的且不会泄露私钥sk_j，可以使用零知识证明（ZKP）技术。
• Link({pk_i}, (S_1, m_1), (S_2, m_2)) -> True/False
  • Link是一个函数，接受公钥集合{pk_i}，两个签名(S_1, m_1)和(S_2, m_2)，输出True或False，表示这两个签名是否由同一个签名者生成。
  • 如果t部分是确定性的，只需检查S_1中的t_1是否等于S_2中的t_2。
• 可以将其推广到一个可链接性的“上下文”中。
  • Link函数接受一个上下文参数，包括“签名事件”、公钥集合{pk_i}、签名(S_1, m_1)和(S_2, m_2)，输出True或False。
  • 解释：甚至可以考虑不同的环用于两个不同的环签名。

上下文

将可链接性推广到一个“上下文”中，意味着我们不仅可以确定两个签名是否由同一个签名者生成，还可以根据特定的上下文信息（例如签名的时间、地点或其他相关的元数据）来进行这种判断。

这样就可以处理更复杂的情况，例如，我们可能想要在特定的时间或地点限制人们的投票行为。

比如，我们可以使用一个Link函数，这个函数接受一个上下文参数（例如当前的日期），公钥集合{pk_i}，以及两个签名(S_1, m_1)和(S_2, m_2)。然后，这个函数会检查这两个签名是否在同一天由同一个人生成。如果是，那么函数就会返回True，表示这两个签名是由同一个人在同一天生成的，否则就返回False。

这就是如何将可链接性推广到一个上下文中的一个例子。这种方法的优点是它可以处理更复杂的情况，而不仅仅是检查两个签名是否由同一个人生成。

Zero-Knowledge (ZK)

证明者P向验证者V证明某个陈述是真实的，而不透露任何其他信息，例如“如何”它是真实的。

• 这个过程确保了验证者只知道陈述的真实性，而不知道证明的具体细节
• 零知识（Zero-Knowledge, ZK）：验证者V可以模拟执行证明过程，但无法说服其他人。
• 换句话说，验证者可以确认证明的真实性，但无法向第三方展示证明过程来证明其真实性。

“论证（Argument）”只有计算健全性，而“证明（Proof）”具有统计（无条件）健全性。

• 论证在计算上是可信的，但在极端情况下可能会被打破；
• 而证明在统计意义上是可信的，即使在无限计算资源下也无法被打破。

如果验证者不需要在线来挑战证明者，那么它是非交互式零知识（Non-Interactive Zero-Knowledge, NIZK）证明。

• 非交互式零知识证明允许证明者一次性提供证明，
• 而验证者可以在任何时间验证该证明，而无需进一步的交互。

Example

Alice需要证明她知道X，但不想泄露X的具体值。传统的证明方法可能会泄露X的值，因此需要一种方法来证明她知道X而不泄露X。

零知识证明（ZKP）可以让Alice证明她知道X，而不泄露任何关于X的信息。这正是零知识证明的核心价值。

1. Alice选择一个随机数R，并计算 Y = R^X mod N，其中N是一个大素数。
2. Alice将 Y 发送给Bob。
3. Bob选择一个随机数 C，并将其发送给Alice。
4. Alice计算Z = R * C^X mod N，并将Z发送给Bob。
5. Bob验证Z是否满足Z^X mod N = Y * C^X mod N。

如果Z满足上述等式，Bob可以确信Alice知道X，而不需要知道X的具体值。

Another ZK Proof Example

• 要证明在两间房间之间存在一条秘密通道。
• 为了进行承诺，验证者（V）在建筑物外等待，而证明者（P）进入其中一个房间。
  这个动作表明P已经选择了一个房间，并准备接受V的挑战。
• 作为挑战，验证者（V）要求证明者（P）从其中一个房间出来。
  这个挑战的目的是测试P是否真的知道秘密通道。
• 健全性：如果P不知道秘密通道，他有50%的概率无法通过测试。通过多次重复这个协议，可以提高验证的可靠性。
• 零知识：任何关于这个证明的视频记录都不会透露关于秘密通道的任何信息，因为可能是P事先知道了V的随机选择。也就是说，视频记录无法证明P是否真正知道秘密通道。

更多细节

这个问题涉及到零知识证明的核心概念。在零知识证明中，证明者（记为P）要向验证者（记为V）证明他们知道某个秘密，但是在证明过程中不会泄露任何关于秘密的信息。

这个特性是通过交互式的证明过程实现的，其中包括随机性和重复性。在每一次交互中，验证者V会随机地选择一个问题让证明者P回答。如果P能正确回答，那么我们就更相信他们知道秘密。然而，因为问题是随机选择的，所以即使P在一次交互中成功回答了问题，也不能确定他们真的知道秘密，因为有可能他们只是碰巧猜对了。

这就是为什么一个单独的视频记录不能证明P知道秘密。视频记录只能展示P在一次或者几次交互中成功回答了问题，但是不能排除他们是碰巧猜对的可能性。只有通过多次重复这个协议，如果P每次都能正确回答，那么我们才能对他们知道秘密有足够的信心。

此外，即使有人看了这个视频，他们也无法学习到关于秘密的任何信息，因为视频中只包含了P回答问题的过程，而没有任何关于秘密本身的信息。这就是零知识证明的"零知识"特性。

多项式时间

在计算机科学和计算复杂性理论中，"多项式时间"（polynomial time）是一种度量算法运行时间复杂性的方式。

如果一个算法的运行时间可以用问题规模 n 的某个多项式函数来界定，那么我们就说这个算法是多项式时间的。

举个例子，如果我们有一个排序算法，对于 n 个元素的列表，它需要 n^2 步来完成排序，那么我们就说这个算法的运行时间是多项式时间的，具体来说是 O*(*n^2)，这是一个多项式函数。

函数 f(n) = n^n 并不是多项式函数。

• 多项式函数的定义是，对于一个非负整数 (n)，函数 $f(n) = a_n n^n + a_{n-1} n^{n-1} + \ldots + a_2 n^2 + a_1 n + a_0$ 是一个多项式函数，其中 $a_0, a_1, \ldots, a_n$ 是常数。
• 因此它被称为超多项式函数（superpolynomial function）。
• 多项式时间算法被认为是“有效可行”的，因为它们的运行时间随着输入规模的增长而增长，但增长的速度相对较慢。
• 这与指数时间算法形成对比，后者的运行时间会随着输入规模的增长而指数级增长，对于较大的输入规模，这种算法通常是不可行的。

在计算复杂性理论中，P类问题就是指可以在多项式时间内解决的问题。

NP

NP是“Nondeterministic Polynomial time”的缩写，意为“非确定性多项式时间”。

NP类问题是指那些在非确定性图灵机（一种理论上的计算模型）上可以在多项式时间内解决的决策问题。

以下是NP问题的一些主要特征：

1. 可验证性：虽然找出NP问题的解可能非常困难，但如果给出一个解，我们可以在多项式时间内检验这个解是否正确。这是NP问题的核心特性。
2. 非确定性：NP问题的解决方案通常需要通过非确定性的方式来寻找，也就是说，我们不能确定怎样的搜索策略可以在多项式时间内找到解。
3. 优化困难：许多NP问题在实际中是优化问题，我们需要找到最优的解。然而，这些问题通常非常难以解决，至今没有找到能在多项式时间内解决所有NP问题的算法。
4. NP完全问题：在NP问题中，有一类特别重要的问题被称为NP完全问题。
   • 如果一个NP问题可以在多项式时间内归约到另一个问题，那么这个问题就被称为NP完全问题。
   • 如果我们能找到一个多项式时间的算法来解决任何一个NP完全问题，那么我们就可以用同样的方法来解决所有的NP问题。这就是著名的P vs NP问题。

P 类问题是指那些可以在多项式时间内解决的决策问题。

• 显然，所有的P类问题也是NP类问题，
• 因为如果一个问题可以在多项式时间内解决，那么它的解也可以在多项式时间内验证。

P vs NP

旅行商问题是一个经典的NP问题。问题的描述如下：

• 给定一组城市和每对城市之间的距离，旅行商需要找到最短的可能路线
• 使得他可以访问每个城市一次并回到原始城市。

这个问题是一个NP问题，因为如果给你一个解决方案（也就是旅行商的旅行路线）

• 你可以在多项式时间内检查这个解决方案是否有效（即是否访问了所有城市并回到了原始城市）以及其长度是否最短。
• 然而，找到这样的最短路线的过程是非常复杂的，至今没有已知的多项式时间算法可以解决这个问题。

关于 P vs NP 问题，它的主要问题是：我们是否能够找到一个多项式时间的算法，可以解决所有的NP问题（包括旅行商问题）。尽管这个问题已经提出了几十年，但计算机科学家们至今还未找到答案。

ZKP Theory/Practice

每个NP陈述都可以通过零知识证明来证明其真实性。

• NP是非确定性多项式时间决策问题（大致上，所有有效可决策的问题）。
• 但用一种通用的方法来做所有类型的证明是低效的。
• 关键点：在理论上总是可行的。
• 关键点：一些定制的方案非常高效。
• 可以将 “或”证明 和 “与”证明 组合在一起。

example

假设有一个密码学问题，Alice想向Bob证明她知道一个大素数的因子分解，但不想泄露任何关于因子的具体信息。

• 这是一个典型的NP问题，因为给定因子分解结果，可以在多项式时间内验证其正确性。
• Alice需要使用零知识证明来证明她知道因子分解，而不泄露任何额外信息。

证明过程

1. Alice选择一个随机数r，并计算r的某个函数值。
2. Alice将这个函数值发送给Bob。
3. Bob随机选择一个挑战。
4. Alice根据挑战计算出一个响应值，并发送给Bob。
5. Bob验证响应值是否正确。

1. 数字签名是一种非交互式的零知识（ZK）论证。
   • 非交互式零知识证明是一种证明方式，其中证明者和验证者不需要多次交互，只需一次性地提供证明数据。
   • 数字签名可以证明消息的真实性和完整性，而不泄露任何额外的信息。
2. 哈希函数“充当”了选择随机值的验证者的角色。
3. 我们将哈希函数视为输出“不可预测”的结果，因为无法找出“简单”的输入输出关系。
4. Schnorr 签名实际上是基于离散对数的私钥知识的零知识论证，而不泄露私钥本身。
5. Schnorr签名通过巧妙的数学构造，允许签名者证明其拥有某个私钥，而不需要公开该私钥。
6. 环签名实际上是关于在n个公钥中拥有某个私钥的零知识论证，而不泄露具体是哪一个私钥。环签名允许签名者在一组公钥中匿名地进行签名，确保签名者的身份隐私。

One-Time Public-Private Key

如何创建一个随机密钥？使用 Diffie-Hellman 密钥交换协议。

• 但发送方不应知道新创建的私钥。
• 想法是将两个离散对数公钥组合为一个公钥。

Pedersen Commitment