布隆过滤器
布隆过滤器
布隆过滤器是一种用于检测集合中是否存在某个元素的数据结构。它通过使用哈希函数和位数组来确定数据的存在性,能够有效地减少缓存穿透的情况。
本文将详细介绍布隆过滤器的原理、应用场景及其在Java项目中的具体实现。
案例背景
为了便于理解,我们以一个真实的电商网站案例进行讲解。假设我们在开发一个类似于淘宝或京东的购物网站,每个商品都有一个唯一的SKU编号。
例如,商品编号857对应的页面内容也是唯一的。
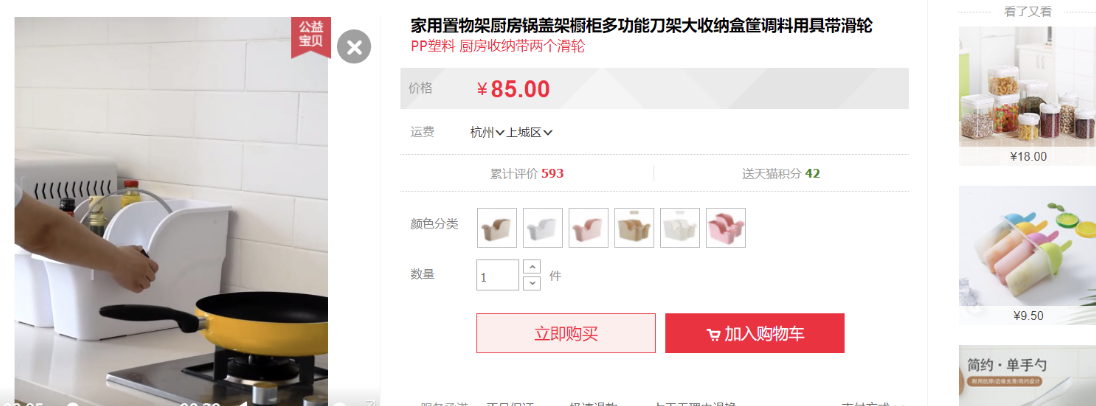
例如在电商平台,下面商品访问的地址为 https://item.jd.com/857.html ,其中 857 是商品的 SKU 。不明白的同学可以简单理解为一个数字对于不同的商品。
系统架构
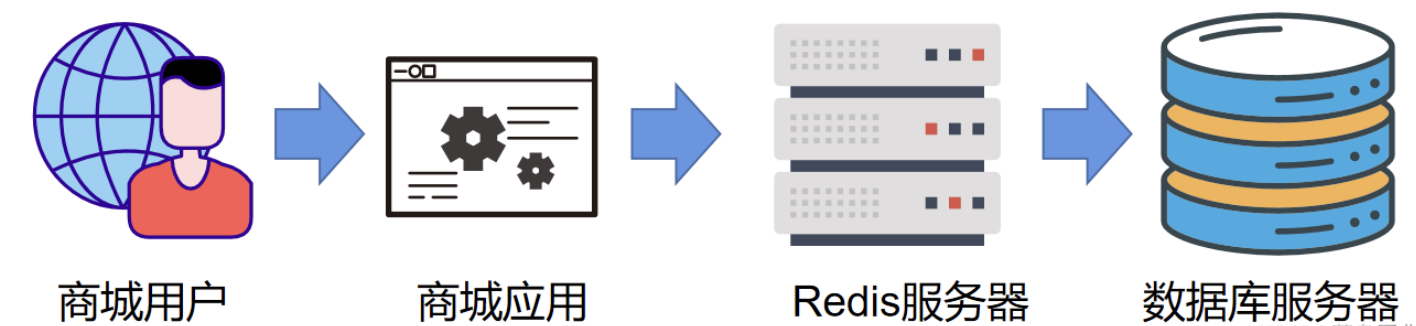
- 用户请求:用户发起一个查看商品的请求,例如查看编号857的商品。
- 缓存查询:商城应用程序首先向后台的Redis缓存服务器进行查询。
- 数据库查询:如果缓存中没有该商品数据,则查询后台的数据库服务器,并将数据填充至Redis缓存。
缓存的优势
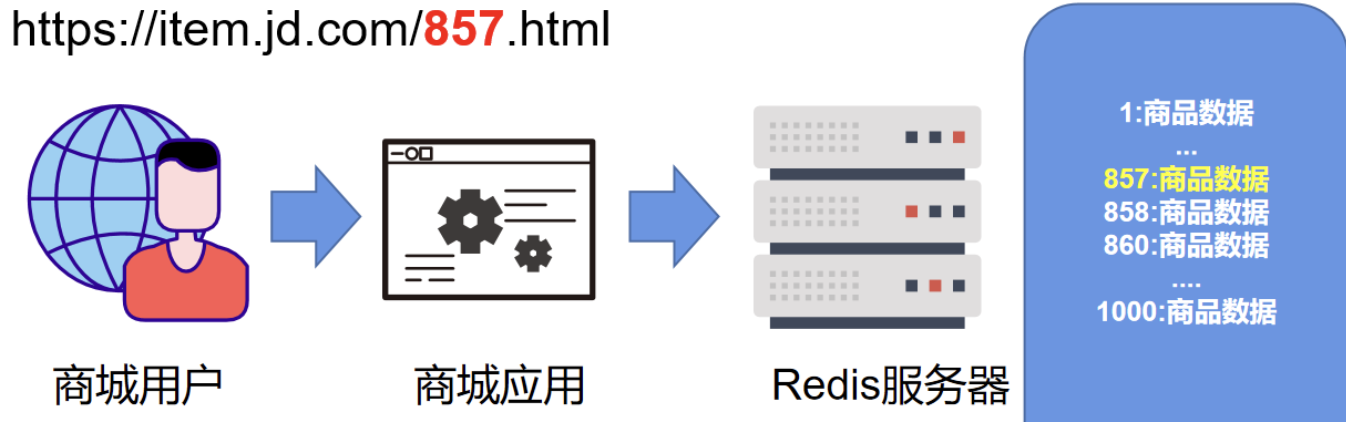
- 性能:Redis基于内存,处理速度和吞吐量远高于传统的MySQL数据库。
- 数据存储:随着时间的积累,Redis缓存中存储了所有商品的数据,避免了频繁的数据库访问。
缓存穿透问题
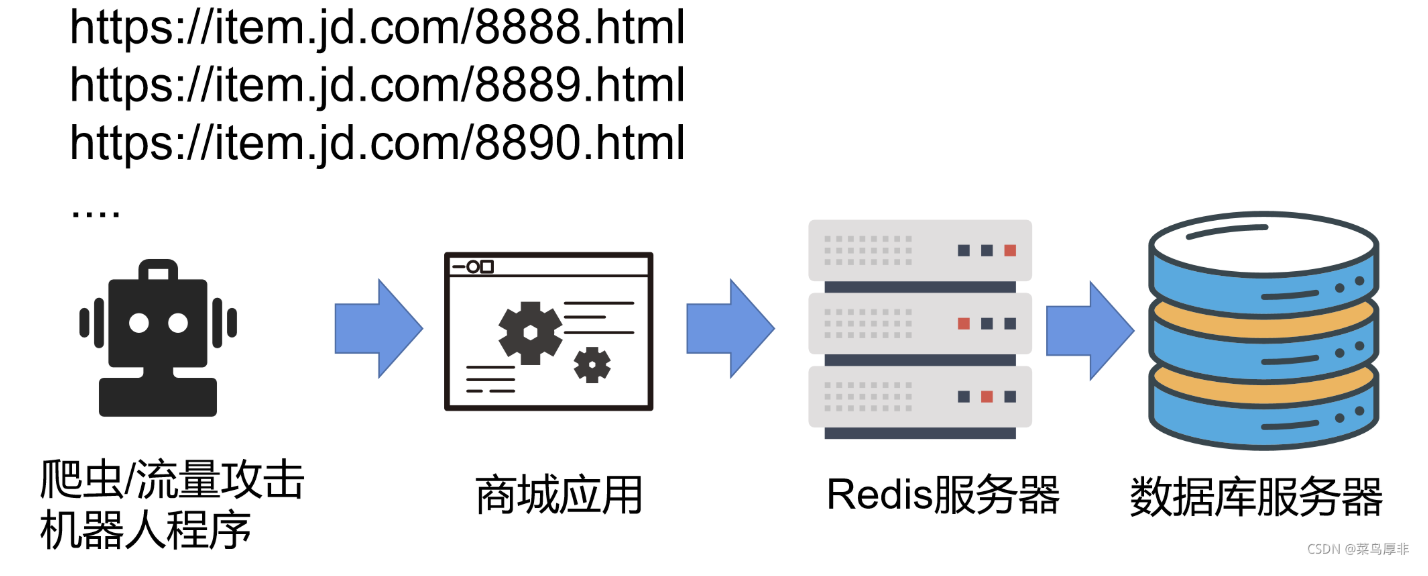
在当前设计下,存在一个致命问题:缓存穿透。假设恶意用户或爬虫机器人在短时间内查询大量不存在的商品编号(如888、889等),这些查询会直接命中数据库,导致数据库服务器超负荷,系统性能下降甚至崩溃。
缓存穿透攻击
- 定义:缓存穿透攻击是指恶意用户在短时间内大量查询不存在的数据,导致大量请求直接命中数据库,超过数据库的负载上限,造成系统高延迟甚至瘫痪。
- 实际案例:多年前的618前夕,我们曾遭遇恶意缓存穿透攻击,导致系统当机两个小时,损失惨重。
布隆过滤器简介
要想预防缓存穿透,可以使用布隆过滤器。那什么是布隆过滤器呢?
布隆过滤器由巴顿·布隆于1970年提出,采用一个长的二进制数组和一系列哈希函数来确定数据是否存在。
- 二进制数组:初始化一个N位的二进制数组,每位初始值为0,存储在Redis中。
- 哈希函数:对每个商品编号进行若干次哈希,确定其在数组中的位置,并将对应位置的值设为1。

操作步骤
- 初始化:对商品编号进行哈希,设置对应位为1。
- 查询存在性:
- 存在:所有哈希位的值都是1。
- 不存在:任何一个哈希位的值为0。
误判问题
布隆过滤器存在小概率的误判,即某些不存在的编号也可能被判定为存在。减少误判的方法包括:
- 增加数组长度:使数据更分散,减少重复。
- 增加哈希次数:增加数据特征,但会增加CPU负担。
布隆过滤器在Java中的应用
Java集成
Java中提供了一个名为redission的组件,内置布隆过滤器,便于开发者使用。
代码示例
// 配置Redis服务器地址和端口号
Config config = new Config();
config.useSingleServer().setAddress("redis://127.0.0.1:6379");
// 实例化Redis客户端
RedissonClient redisson = Redisson.create(config);
// 创建布隆过滤器对象
RBloomFilter<Integer> bloomFilter = redisson.getBloomFilter("sampleBloomFilter");
// 初始化布隆过滤器
bloomFilter.tryInit(1000000L, 0.01);
// 添加数据
bloomFilter.add(1);
// 判断数据是否存在
boolean exists = bloomFilter.contains(1); // true
boolean notExists = bloomFilter.contains(8888); // false
参数说明
- 初始化长度:布隆过滤器的预计元素为 1000000L长度,设置的长度越大,误判率越低。
- 误判率:期望最大允许的误判率,通常设置为1%。
项目中的布隆过滤器使用流程
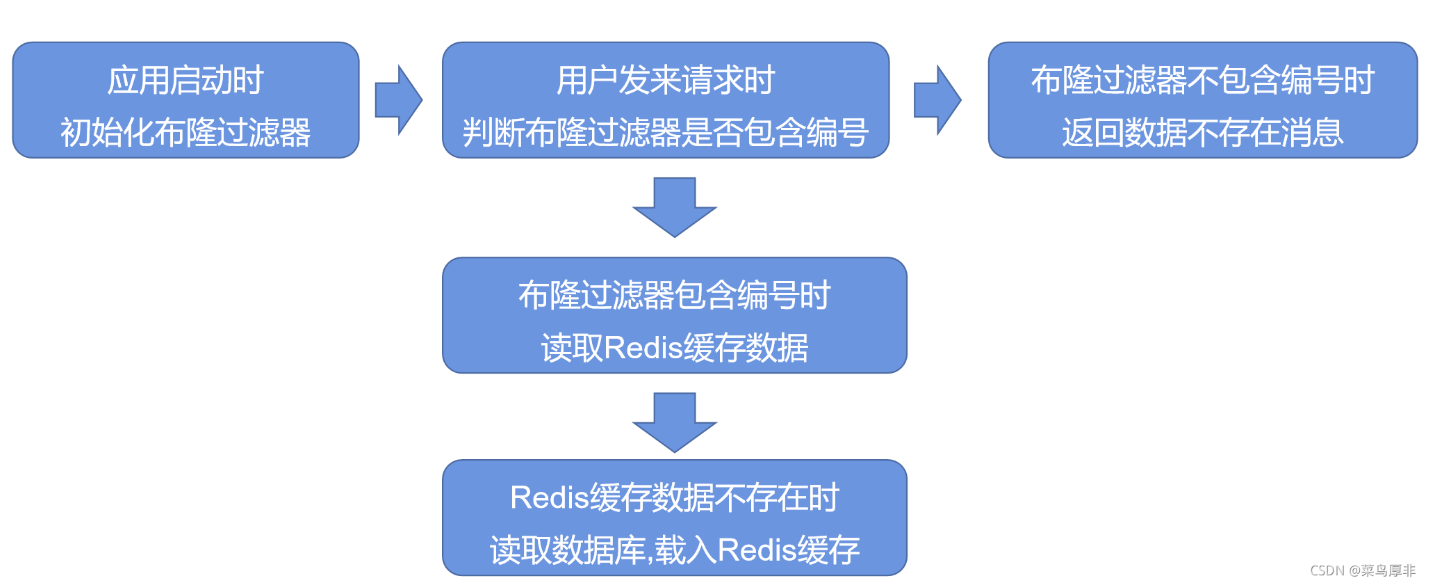
初始化阶段
在应用启动时,初始化布隆过滤器,将所有商品编号进行哈希处理,设置二进制数组。
请求处理
- 存在编号:直接读取Redis缓存数据,如果缓存中没有,则查询数据库并更新缓存。
- 不存在编号:布隆过滤器判断数据不存在,直接返回提示信息,避免数据库查询。
误判处理
尽管布隆过滤器存在误判,但在大多数情况下不会对系统产生重大影响。设置合适的误判率(如1%),可以有效拦截99%的无效请求,减少系统负担。
布隆过滤器数据删除问题
布隆过滤器某一位可能被多个编号引用,直接删除某一位会导致数据混乱。
解决方案
- 定时异步重建:定期在额外服务器上异步重建布隆过滤器,替换已有的布隆过滤器。
- 计数布隆过滤器:在标准布隆过滤器基础上增加计数信息,记录每个位被引用的次数。
总结
布隆过滤器是一种高效的缓存穿透防护手段,通过合理的初始化和使用,可以大幅提升系统的性能和稳定性。
尽管存在误判,但通过增加数组长度和哈希次数,可以有效降低误判率。在实际项目中,布隆过滤器的应用流程简单且高效,是一种值得推广的技术。
QA
对于布隆过滤器,有个同学在学习完相关概念之后,问了一个问题,说如何平衡布隆过滤器的1 和 0 的量?假设数据一致增加,布隆过滤器迟早会出现所有的数字位都为1的情况。
首先,这个问题的关键在于控制布隆过滤器的误报率。误报率主要取决于四个因素:布隆过滤器的位数m、哈希函数的个数k、插入的元素个数n、以及1和0的比例。如果布隆过滤器的位数过小,或者哈希函数的个数过多,或者插入的元素过多,都会导致误报率上升。
对于你提到的问题,如果数据一直增加,布隆过滤器迟早会出现所有的数字位都为1的情况,这是正确的。当所有位都变为1时,布隆过滤器的误报率将达到100%,这时布隆过滤器就失去了其应有的功能。为了避免这种情况,我们可以采取以下策略:
- 扩容:当布隆过滤器的负载因子(即1的比例)达到一定阈值时,可以考虑增加布隆过滤器的位数。这样可以降低1的比例,从而降低误报率。
- 重新哈希:当布隆过滤器的负载因子达到一定阈值时,可以考虑将所有元素重新哈希到一个新的、更大的布隆过滤器中。这样也可以
请问 redison 是怎么平衡的?
在 Redisson 中,布隆过滤器的大小和哈希函数的数量在初始化时就确定了,并且在后续的使用中不会发生改变。初始化时,你需要指定预计要插入的元素数量和期望的误报率,然后 Redisson 会根据这两个参数计算出最优的布隆过滤器大小和哈希函数数量。
在你的例子中,bloomFilter.tryInit(1000000L, 0.01); 这行代码的意思是,你预计要插入的元素数量是1000000,期望的误报率是0.01(即1%)。然后 Redisson 会根据这两个参数计算出最优的布隆过滤器大小和哈希函数数量。
但是,如果实际插入的元素数量超过了预计的数量,那么误报率就会上升。因为布隆过滤器的大小和哈希函数的数量在初始化时就确定了,所以在 Redisson 中,如果实际插入的元素数量超过了预计的数量,你无法通过扩容或重新哈希来降低误报率。
对于布隆过滤器,有个同学在学习完相关概念之后,提出了一个新的理念,叫双重布隆过滤器,
就是A过滤器,对于 存在的元素设置为相应1,
B过滤器,对于 不存在的元素设置为相应1,
他声称这样结合后以百分百判断,你认为他的说法对吗,为什么?
这个同学的想法很有创意,但是他的方法在实际应用中可能并不会像他想象的那样有效。
首先,我们需要理解布隆过滤器的基本原理。布隆过滤器是一种空间效率极高的概率数据结构,用于测试一个元素是否在集合中。它的主要优点是空间效率和查询时间都极其优秀,但是这是以一定的误报率为代价的。也就是说,布隆过滤器可能会错误地认为一个元素在集合中(false positive),但绝不会错误地认为一个元素不在集合中(false negative)。
在你的同学的设想中,A过滤器和B过滤器分别处理存在的元素和不存在的元素。然而,这种方法存在一些问题:
对于A过滤器,我们可以很容易地将存在的元素设置为1。但是对于B过滤器,我们如何知道哪些元素不存在呢?实际上,不存在的元素的数量是无穷大的,我们无法将所有不存在的元素都设置为1。
即使我们可以确定某些元素肯定不存在(例如,我们正在处理的是一组有限的元素,我们知道哪些元素不在这个集合中),B过滤器仍然会有false positive的问题。也就是说,它可能会错误地认为某个元素不存在。
假设我们有一种方法可以完美地处理不存在的元素,那么这种“双重布隆过滤器”实际上就变成了一个完全精确的数据结构,如哈希表或集合,而不再是布隆过滤器。这种数据结构的空间效率和查询时间可能都不如布隆过滤器。
综上所述,虽然这个想法很有创意,但是在实际应用中可能并不可行。
同时使用多个布隆过滤器会提高准确率吗?
即出现了 True 的结果就继续挑战另一个过滤器。
使用多个布隆过滤器来提高准确率的性价比取决于具体的应用场景和需求。这主要涉及到以下几个因素:
误判率的重要性:如果应用场景中误判的代价非常高,那么使用多个布隆过滤器来降低误判率可能是值得的。例如,在某些安全敏感的场景中,我们可能更愿意牺牲一些性能和空间来换取更低的误判率。
空间和性能的限制:如果应用场景中对空间和性能有严格的限制,那么使用多个布隆过滤器可能不太适合。因为每增加一个过滤器,都会增加相应的空间和性能开销。
数据的特性:如果数据的分布和特性使得误判率本身就比较低,那么使用多个布隆过滤器可能没有太大的必要。反之,如果数据的特性使得误判率比较高,那么使用多个过滤器可能会有较大的帮助。
总的来说,是否使用多个布隆过滤器,以及使用多少个,需要根据具体的应用场景和需求来决定。在实际使用时,可能需要通过实验和调优来找到最佳的策略。
使用多个布隆过滤器来提高准确率的性价比取决于具体的应用场景和需求。这主要涉及到以下几个因素:
误判率的重要性:如果应用场景中误判的代价非常高,那么使用多个布隆过滤器来降低误判率可能是值得的。例如,在某些安全敏感的场景中,我们可能更愿意牺牲一些性能和空间来换取更低的误判率。
空间和性能的限制:如果应用场景中对空间和性能有严格的限制,那么使用多个布隆过滤器可能不太适合。因为每增加一个过滤器,都会增加相应的空间和性能开销。
数据的特性:如果数据的分布和特性使得误判率本身就比较低,那么使用多个布隆过滤器可能没有太大的必要。反之,如果数据的特性使得误判率比较高,那么使用多个过滤器可能会有较大的帮助。
总的来说,是否使用多个布隆过滤器,以及使用多少个,需要根据具体的应用场景和需求来决定。在实际使用时,可能需要通过实验和调优来找到最佳的策略。