Regression to the mean
大约 8 分钟
Regression to the mean
概念
回归均值「Regression to the mean」是数据的一种属性/特性,不是一种模型。下面有一些常见的例子:
- 如果你最喜欢的运动队去年赢得了冠军,这对他们下赛季获胜的机会意味着什么?在某种程度上,这个结果是由于技术(球队状况良好,有顶级教练等),他们的胜利表明他们更有可能在明年再次获胜。但这在很大程度上是由于运气(其他球队卷入毒品丑闻、有利局等),他们明年再次获胜的可能性就越小。
- 如果一个商业组织有一个高利润的季度,尽管其业绩的根本原因没有改变,它可能在下个季度表现不佳。
- 在新赛季打得很好的棒球运动员可能会在第二个赛季打得更差.
在统计学中,回归均值(也称为回归均值和回归平庸)是一个概念,它指的是如果随机变量的一个样本是极端的,那么同一随机变量的下一个样本很可能更接近其平均值。
不要与均值回归的金融概念混淆。
我们可以使用线性回归来量化均值回归的影响。
均值回归的概念
您已经看到数据集中的每个响应值都等于拟合值的总和,即模型的预测值和残差,即模型遗漏了多少。笼统地说,这两个值是反应中你已经解释了它为什么有这个值的部分,以及你无法用模型解释的部分。
为什么你有残差有两种可能性。首先,这可能只是因为您的模型不是很好。特别是在只有一个解释变量的简单线性回归的情况下,通常还有改进的余地。然而,拥有一个完美的模型通常是不可能或不可取的,因为世界包含很多随机性,而您的模型不应该捕捉到它。特别是,极端反应通常是由于随机性或运气。这意味着极端情况不会随着时间的推移而持续存在,因为最终运气会耗尽。这就是回归均值的概念。最终,极端情况看起来更像一般情况。
举例说明
回归均值是包括体育在内的许多领域的重要概念。
这里你可以看到2017年和2018年的棒球击球数据集。每个点代表一个球员,更多的全垒打是更好的。一个天真的预测可能是,2018年的表现与2017年的表现相同。也就是说,线性回归将位于 "y等于x "的线上。
探索该图并作出预测。对于一个在2017年非常成功的球员来说,回归均值对2018年的全垒打数量有什么意义?
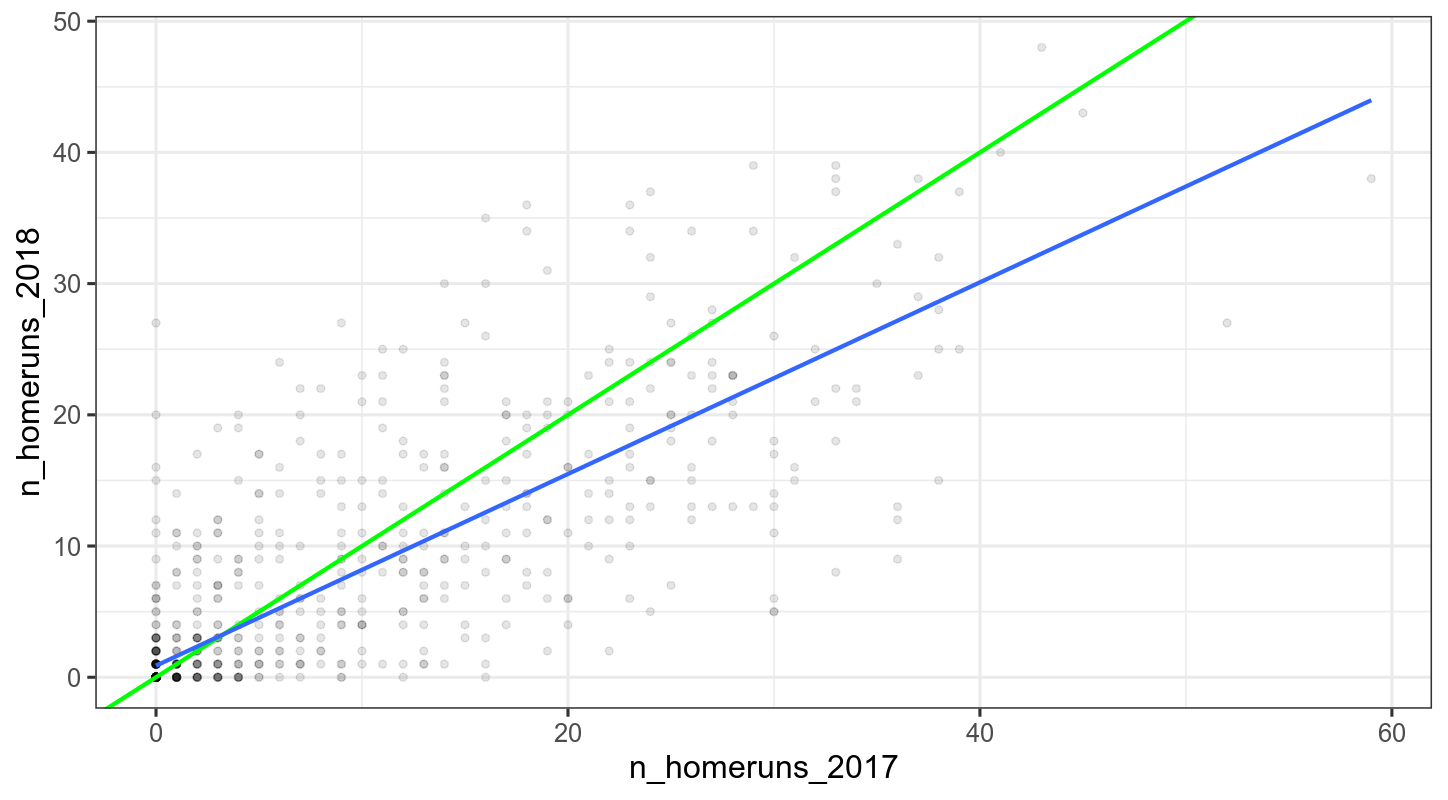
解释:一个在2017年打出40支全垒打的人被预测在下一年会少打10支全垒打,因为向平均值回归说明,平均而言,极高的数值是无法持续的。