Quantifying model fit

即「量化模型拟合」

r-squared

又称「Coefficient of determination」，即测定系数

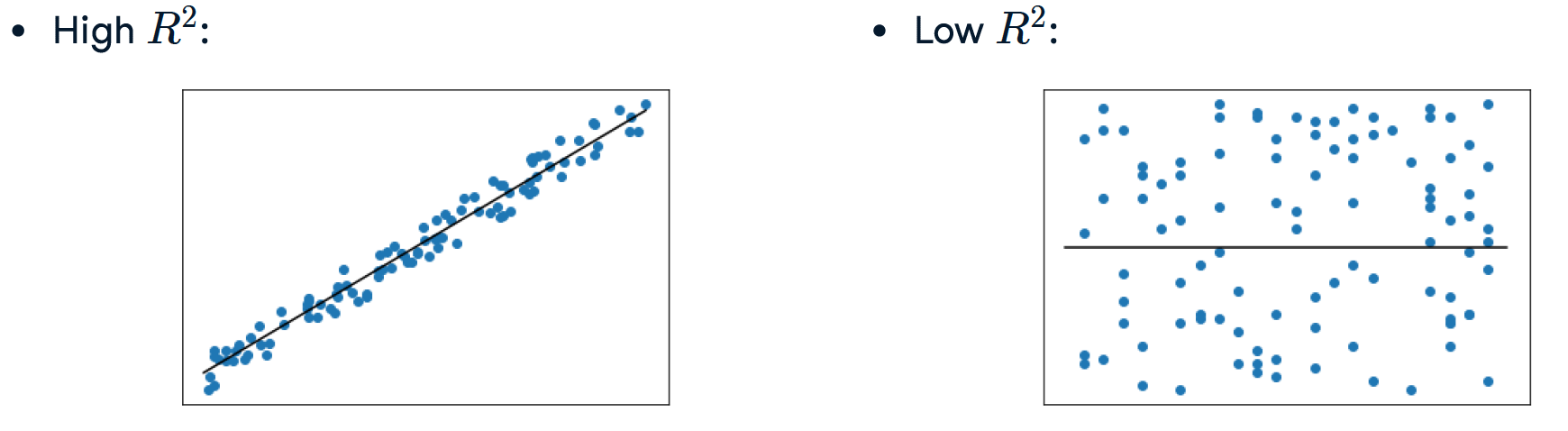
由于枯燥的历史原因，简单的线性回归用小写的r，当你有一个以上的解释变量时用大写的R。它被定义为响应变量中可由解释变量预测的方差比例。

判定系数R²是评估回归模型好坏的指标。R平方取值范围也为0~1，通常以百分数表示。比如回归模型的R平方等于0.7，那么表示，此回归模型对预测结果的可解释程度为70%。

1655368557189.png

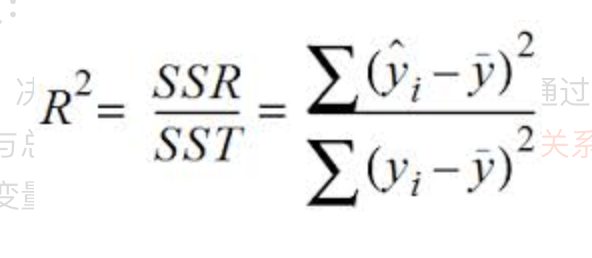
使用 .summary() 查看

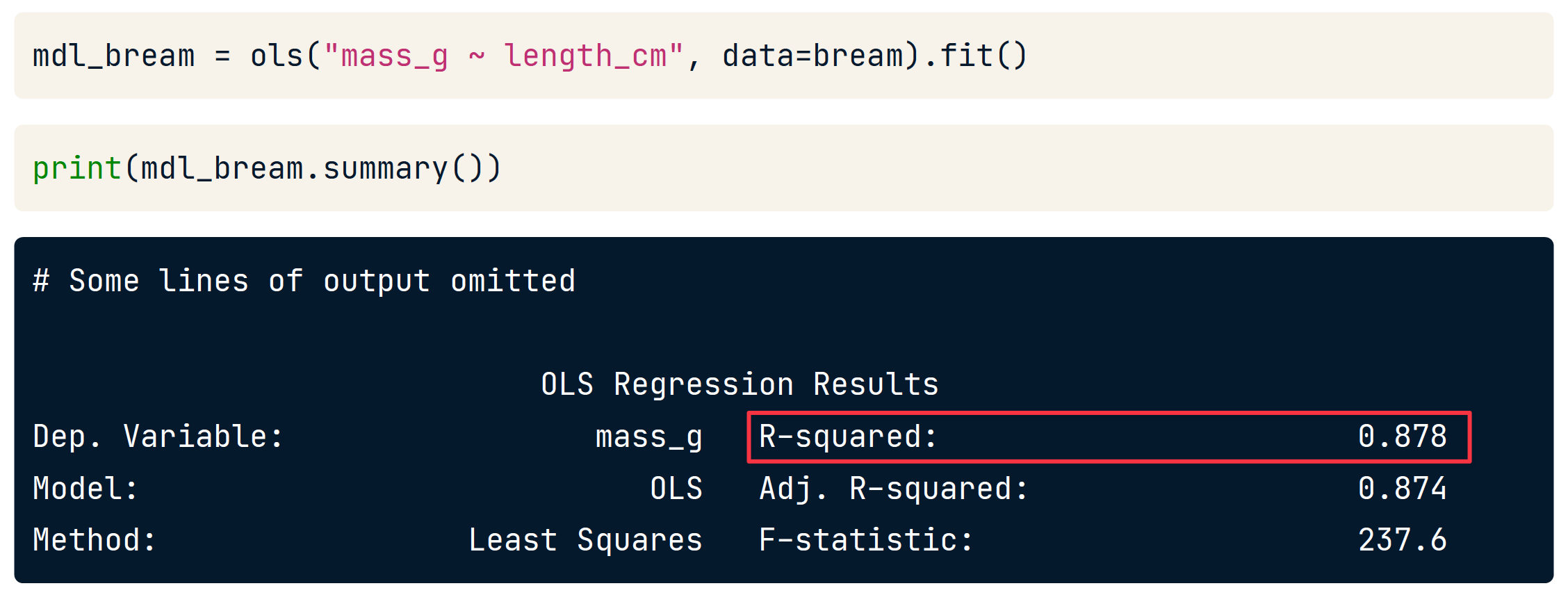
可通过 .rsquared 计算

print(mdl_bream.rsquared)

0.8780627095147174

公式推导

对于线性回归模型，r² 就是 correlation squared。

coeff_determination = bream["length_cm"].corr(bream["mass_g"]) ** 2
print(coeff_determination)

0.8780627095147173

r^2 的公式 可由相关系数公式推导出来。下面是相关系数r的计算公式。

MSE & RMSE

1656096974109.png

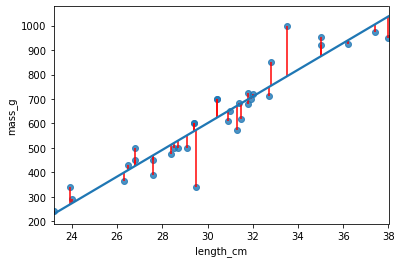
• Mean squared error「平均平方误差」
• root mean squared error「平均平方根误差」:残差标准误差（RSE）是对残差的典型大小的衡量。等于说，它是一个衡量你可以期望预测的错误程度的指标。数字越小越好，零是对数据的完美拟合。

RMSE² = MSE

计算 MSE

mse = mdl_bream.mse_resid
print('mse: ', mse)

mse: 5498.555084973521

手动计算 RSE

RSE样本求均值

RMSE 的是总体求均值，RSE是样本求均值。

如果是“总体”求平均，那么分母是除以总体的个数。但如果是样本求平均的话，由于样本的目的是估计总体，所以这个时候要对分母进行调整从而使估计更准确。分母不再是除以样本个数，而是除以自由度。这样做的可以使样本估计量满足一致性，进而更准确的估计总体。

至于自由度是多少这个很难拿语言描述清楚，也没有必要去了解甚至证明，直接当做结论记住即可。

最常用的自由度是t检验的自由度为n-k-1，也就是样本数量n减去要估计的参数（K+1），其中k是要估计的k个slope coefficient，即b1，b2....bk，而“1”是要估计的1个intercept，即b0。一元线性回归，自由度 = n - 2

我们通常应当使用 RSE公式 而不是 RMSE公式。

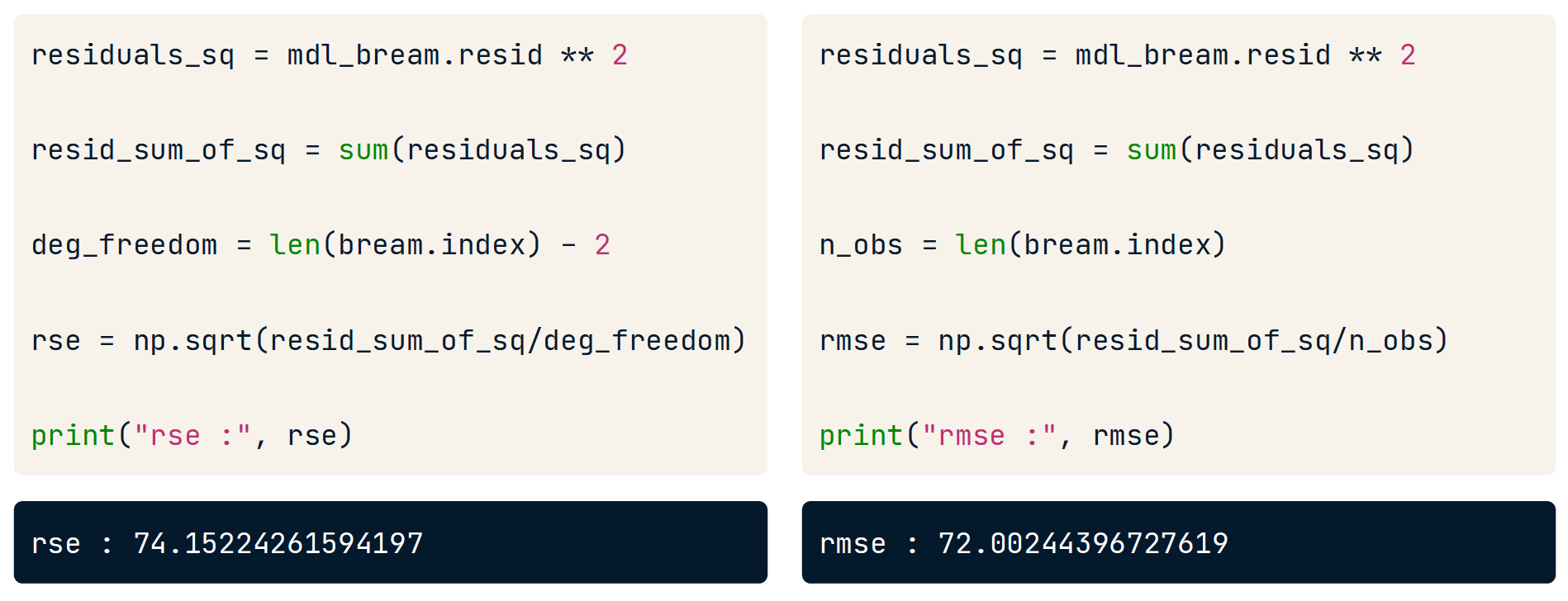
# 计算残差，生成残差series, residuals = mdl_bream.resid
# mdl_bream 是 fit() 后的模型
residuals_sq = mdl_bream.resid ** 2
resid_sum_of_sq = sum(residuals_sq)
# deg_freedom = 33 - 2
rse = np.sqrt(resid_sum_of_sq/deg_freedom)
print("rse :", rse)

rse : 74.15224261594197

解释 RSE 的案例：预测的鲷鱼质量和观察到的鲷鱼质量之间的差异通常约为 74 克。(RSE 是与响应变量相关的度量，而不是解释变量。)

手动计算 RMSE