Visualizing model fit
Visualizing model fit
残差图
残差中的非随机模式表明模型的确定部分(预测变量)没有捕获一些“泄露”到残差中的一些可解释/可预测信息。表明模型几种没法解释的可能性,可能性包括:一个缺失的变量:
- 模型缺少一个变量的高阶项来解释曲率。
- 模型缺少在已经存在的项之间的相互作用项(交叉项)
由此来回溯去修改模型,以期望修改后的残差图是理想中的残差图。除了上述之外,还有两种预测信息会潜入到了残差中的方式:
- 残差不应该与另外的变量有所相关。如果你可以用另一个变量预测出此残差图,那么该变量就应该考虑到你的模型当中。那么就可以通过绘制其他变量的残差图,来考察这个问题。
- 相邻残差(Adjacent residuals)不应该相互关联(残差的自相关性)。如果你可以使用一个残差来预测得到下一个残差,则说明存在一些模型还未捕捉到的可预测信息。通常来说,这种情况涉及时间有序的观察预测。
综上,若非要一句话小结,那就是要留意:正确残差图不仅要体现出随机性(random),还要体现不可预测性(unpredictable)即可。
残差图是指以残差为纵坐标,以任何其他指定的量为横坐标的散点图。(上图仅是残差的示意图,非残差图,残差图可见下文)。
用普通最小二乘法(OLS)做回归分析的人都知道,回归分析后的结果一定要用**残差图(residual plots)**来检查,以验证你的模型。你有没有想过这究竟是为什么?残差图又究竟是怎么看的呢?
这背后当然有数学上的原因,但是这里将着重于聊聊概念上的理解。从根本上说,随机性(randomness)和不可预测性(unpredictability)是任何回归模型的关键组成部分,如果你没有考虑到这两点,那么你的模型就不可信了,甚至说是无效的。
为什么这么说呢?首先,对于一个有效的回归模型来说:响应(Response) = 确定性(Deterministic) + 随机性(Stochastic)
随机误差(The Stochastic Error)
Stochastic 这个词很牛逼,其不仅蕴含着随机性(random),还有不可预测性(unpredictable)。这是很重要的两点,往往很多朋友都以为有随机性的特点就够了,其实不然。这两点放在一起,就是在告诉我们回归模型下的预测值和观测值之间的差异必须是随机不可预测的。换句话说,在误差(error)中不应该含有任何可解释、可预测的信息。
模型中的确定性部分应该是可以很好的解释或预测任何现实世界中固有的随机响应。如果你在随机误差中发现有可解释的、可预测的信息,那就说明你的预测模型缺少了些可预测信息。那么残差图(residual plots)就可以帮助你检查是否如此了!
我们可以用残差图来估计观察或预测到的误差error(残差residuals)与随机误差(stochastic error)是否一致。如果残差符合其均值为零的正态分布的假设,那么趋势线应该紧跟图上的y等于零线。
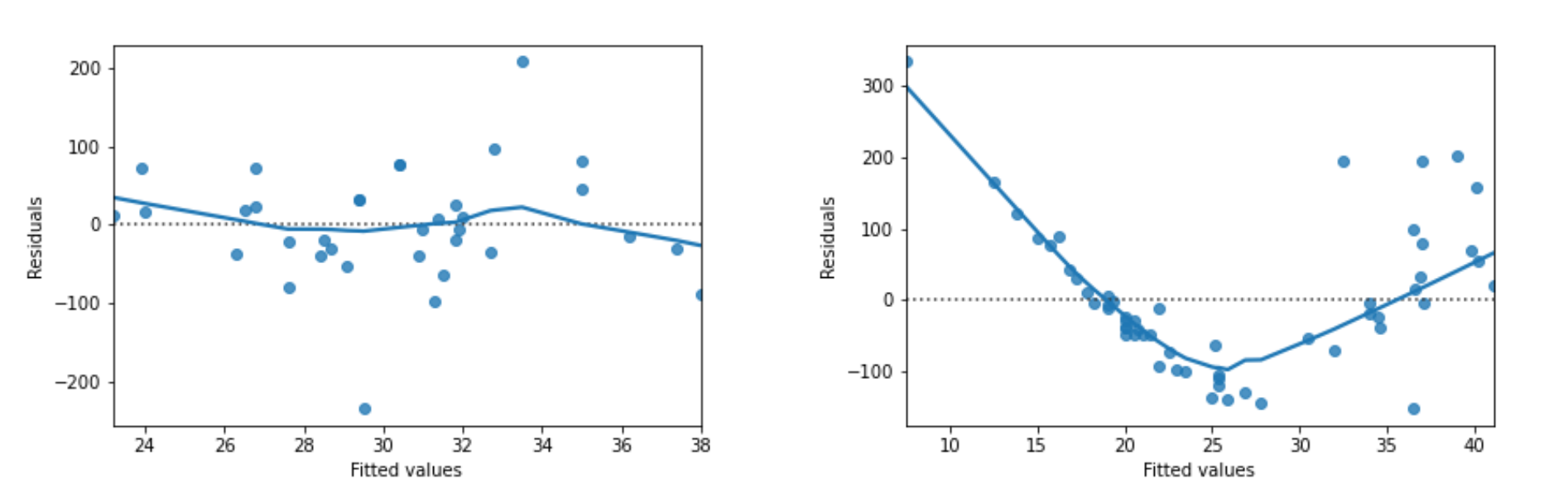
我们在鳊鱼和鲈鱼的数据集上运行模型。通过观察带有线性趋势线的散点图,似乎鳊鱼模型是一个很好的拟合,但鲈鱼模型不是,因为观察到的质量增加速度超过了与长度的线性关系。
# Plot the residuals vs. fitted values
sns.residplot(x="n_convenience", y="price_twd_msq", data=taiwan_real_estate, lowess=True)
plt.xlabel("Fitted values")
plt.ylabel("Residuals")
# Show the plot
plt.show()
QQ plot
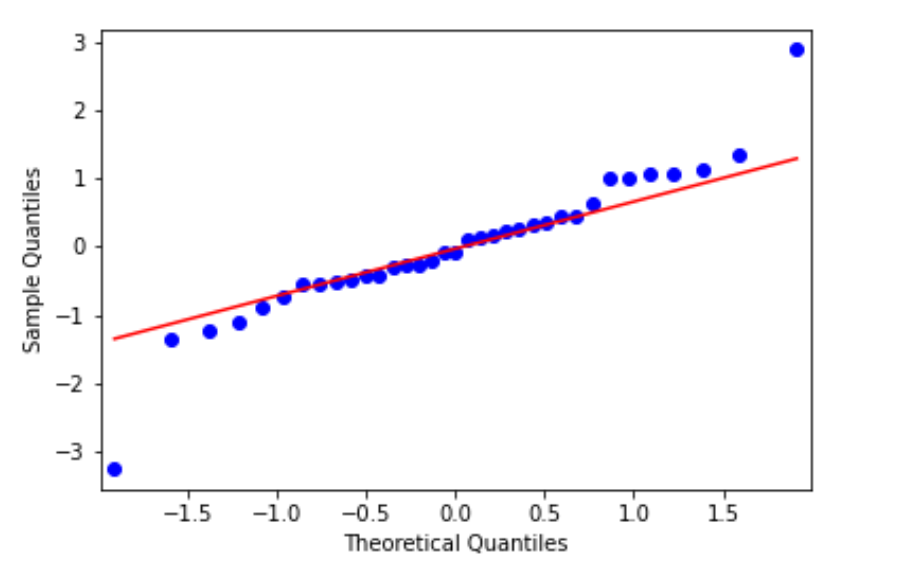
如果这些点沿着直线追踪,它们就是正态分布。如果不是,它们就不是。
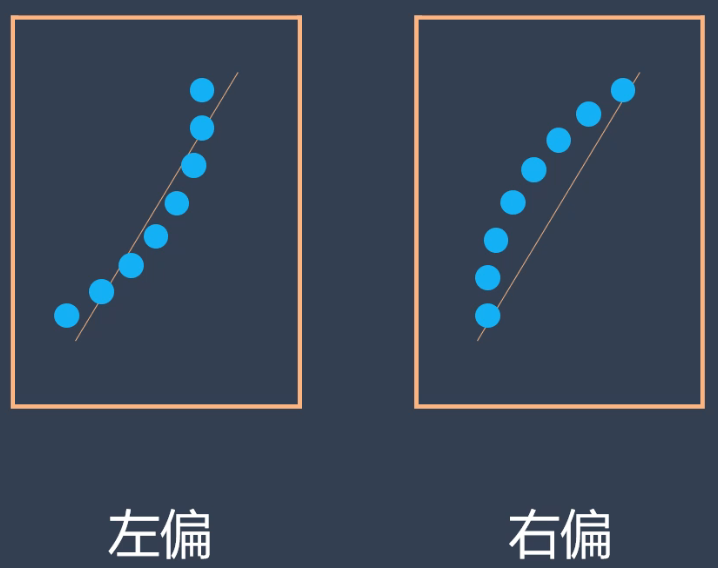
# Import qqplot
from statsmodels.api import qqplot
# Create the Q-Q plot of the residuals
qqplot(data=mdl_price_vs_conv.resid, fit=True, line="45")
# Show the plot
plt.show()
Scale-location plot
解释和残差图的解释相似
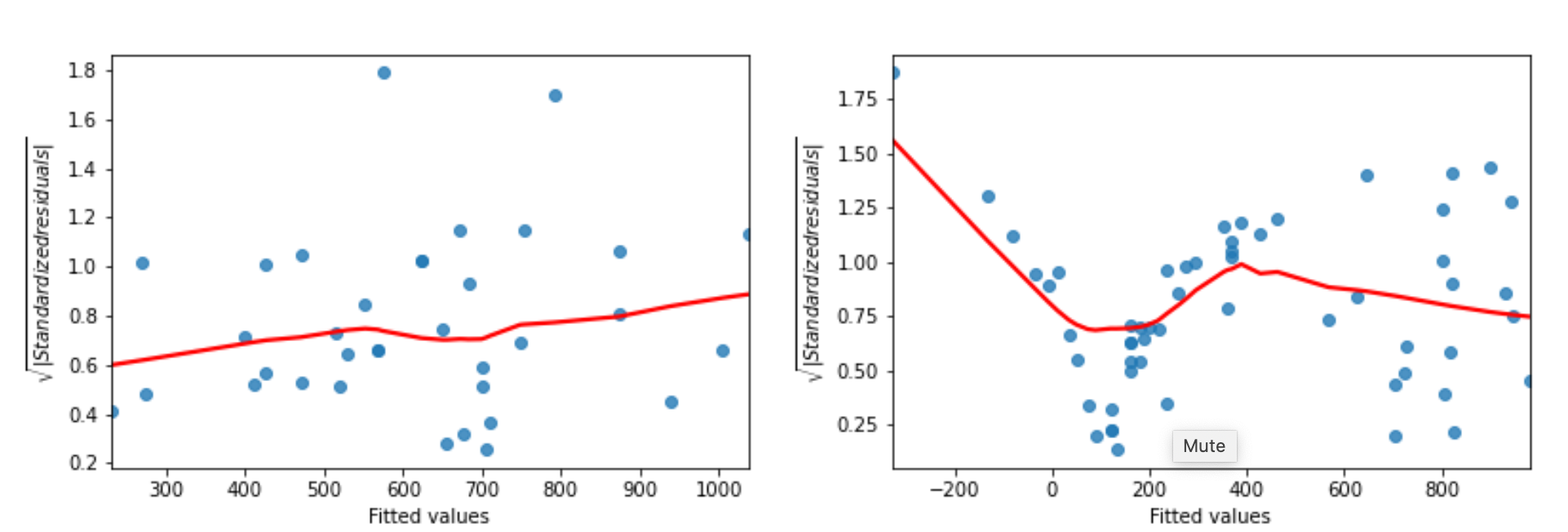
# Preprocessing steps
model_norm_residuals = mdl_price_vs_conv.get_influence().resid_studentized_internal
model_norm_residuals_abs_sqrt = np.sqrt(np.abs(model_norm_residuals))
# Create the scale-location plot
sns.regplot(x=mdl_price_vs_conv.fittedvalues, y=model_norm_residuals_abs_sqrt, ci=None, lowess=True)
plt.xlabel("Fitted values")
plt.ylabel("Sqrt of abs val of stdized residuals")
# Show the plot
plt.show()