Hyperparameter tuning

• Ridge/lasso regression: Choosing alpha
• KNN: Choosing n_neighbors

Choosing the correct hyperparameters：

1. Try lots of di(erent hyperparameter values
2. Fit all of them separately
3. See how well they perform
4. Choose the best performing values

这个过程被称为 hyperparameter tuning

1. 必须使用交叉验证来避免过度使用测试集
2. 我们仍然可以拆分数据并对训练集进行交叉验证
3. 我们保留用于最终评估的测试集

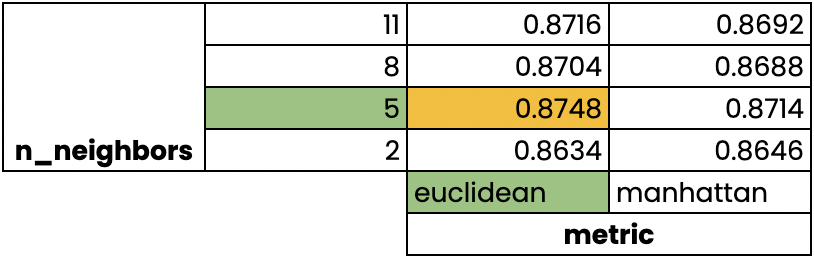
GridSearchCV in sk

网格搜索+交叉验证，搜索的是参数，即在指定的参数范围内，按步长依次调整参数，利用调整的参数训练学习器，从所有的参数中找到在验证集上精度最高的参数，这其实是一个循环和比较的过程。

from sklearn.model_selection import GridSearchCV

kf = KFold(n_splits=5, shuffle=True, random_state=42)
param_grid = {"alpha": np.arange(0.0001, 1, 10), "solver": ["sag", "lsqr"]}
ridge = Ridge()
ridge_cv = GridSearchCV(ridge, param_grid, cv=kf)

ridge_cv.fit(X_train, y_train)
print(ridge_cv.best_params_, ridge_cv.best_score_)

{'alpha': 0.0001, 'solver': 'sag'}
0.7529912278705785

Limitations and an alternative approach

• 3-fold cross-validation, 1 hyperparameter, 10 total values = 30 ,ts
• 10 fold cross-validation, 3 hyperparameters, 30 total values = 900 ,ts

RandomizedSearchCV

在超参数空间搜索几十几百个点，其中就有可能比较小的值，比稀疏化网络的做法快，而且实验证明，随机搜索结果比稀疏网络法稍好。随机搜索不是尝试所有可能的组合，而是通过选择每一个超参数的随机值的特定数量的随机组合，有两个优点：比如运行1000次，中探索每个超参数的1000个不同的值；通过设定搜索次数，控制超参数搜索的计算量。

from sklearn.model_selection import RandomizedSearchCV

kf = KFold(n_splits=5, shuffle=True, random_state=42)
param_grid = {'alpha': np.arange(0.0001, 1, 10), "solver": ['sag', 'lsqr']}
ridge = Ridge()
ridge_cv = RandomizedSearchCV(ridge, param_grid, cv=kf, n_iter=2)

# Checking model parameters
ridge_cv.fit(X_train, y_train)
print(ridge_cv.best_params_, ridge_cv.best_score_)

{'solver': 'sag', 'alpha': 0.0001}
0.7529912278705785

Evaluating on the test set

# ridge_cv 将会挑选最佳参数计算测试集的得分
test_score = ridge_cv.score(X_test, y_test)
print(test_score)

0.7564731534089224