Linear Regression
Linear Regression
一元回归
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X_bmi, y)
predictions = reg.predict(X_bmi)
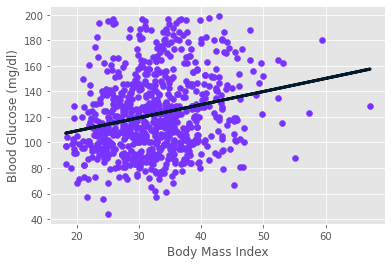
plt.scatter(X_bmi, y)
plt.plot(X_bmi, predictions)
plt.ylabel("Blood Glucose (mg/dl)")
plt.xlabel("Body Mass Index")
plt.show()
一元一次回归机制

How do we choose a and b?
- Define an error function for any given line
- Choose the line that minimizes the error function
Error function = loss function = cost function
对于一元一次回归方程参数的求解,我们可以使用 普通最小二乘法 来计算 cost
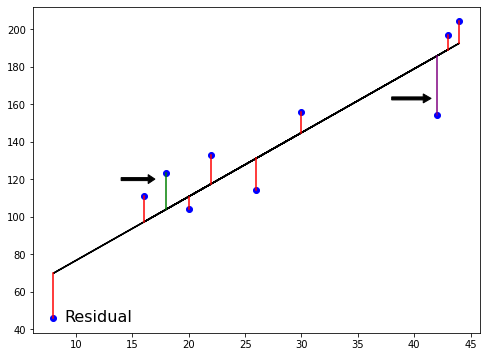
Ordinary Least Squares (OLS): minimize RSS, 「普通最小二乘法(OLS):最小化RSS」
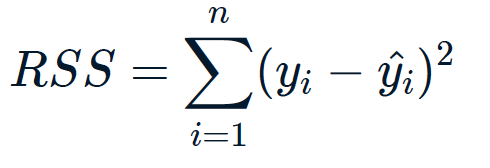
回归直线应满足的条件是:全部观测值与对应的回归估计值的误差平方和最小,即:

其实就是一个用积分求最小值的过程。
多元回归
Linear regression in higher dimensions

如何定义 cost function 以及求解 cost function的最小值,将在后续章节解释。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
reg_all = LinearRegression()
reg_all.fit(X_train, y_train)
y_pred = reg_all.predict(X_test)
Cross validation
不同的训练数据和测试数据的拆分方式会影响拟合的结果
- 模型性能取决于我们拆分数据的方式
- 不代表模型泛化到看不见的数据的能力
可以通过拆分数据成为不同块然后组合。最终的结果是这 k 次验证的均值。

交叉验证和模型性能:More folds = More computationally expensive
- 5 folds = 5-fold CV
- 10 folds = 10-fold CV
- k folds = k-fold CV
实际生产中,10折交叉验证方法最为常见。
Cross-validation in scikit-learn:
from sklearn.model_selection import cross_val_score, KFold
kf = KFold(n_splits=6, shuffle=True, random_state=42)
reg = LinearRegression()
cv_results = cross_val_score(reg, X, y, cv=kf)
print(cv_results)
[0.70262578, 0.7659624, 0.75188205, 0.76914482, 0.72551151, 0.73608277]
print(np.mean(cv_results), np.std(cv_results))
0.7418682216666667 0.023330243960652888
print(np.quantile(cv_results, [0.025, 0.975]))
array([0.7054865, 0.76874702])
提示
scikit-learn 的交叉验证指标假定分数越高越好,因此可以将 MSE 更改为负数以抵消这种情况。
提示
尽管 cross_val_score 已经包含了拆分、拟合、预测和评分四个过程,但在 KFold 之前依然可以先通过 train_test_split 把数据拆分一下。这样 cross_val_score 将把 train_test_split 后的 训练数据集 再拆分成 训练 和 测试集。
Leave-One-Out Cross-Validation
假定数据集D中包含m个样本,若令k=m,则得到了交叉验证法的一个特例:留一法(Leave-One-Out,简称LOO)。
留一法交叉验证(Leave-One-Out Cross-Validation,LOO-CV)是贝叶斯模型比较重常见的一种方法。
顾名思义,就是使 k 等于数据集中数据的个数,每次只使用一个作为测试集,剩下的全部作为训练集,
留一法交叉验证,它是k折交叉验证的一种特例,因为它可以看做是当k等于样本量n时的n折交叉验证。这意味着每一个数据点都被用来测试,而所有剩下的(n-1)个数据点为相应的测试集。
留一法使用的训练集与初始数据集相比只少了一个样本,这就使得在绝大多数情况下,留一法中被实际评估的模型与期望评估的用D训练出的模型很相似。因此,留一法的评估结果往往被认为比较准确。
然而,留一法也有其缺陷:在数据集比较大时,训练m个模型的计算开销可能是难以忍受的(例如数据集包含1百万个样本,则需训练1百万个模型),而这还是在未考虑算法调参的情况下。另外,留一法的估计结果也未必永远比其他评估方法准确;“没有免费的午餐”定理对实验评估方法同样适用。
Regularized regression
Ridge regression
- Loss function = OLS loss function +
- 岭惩罚大的正或负系数
- α: parameter we need to choose
- Picking α is similar to picking k in KNN
- α controls model complexity
- α = 0 = OLS (Can lead to overfitting)
- Very high α: (Can lead to underfitting)
- 超参数:用于优化模型参数的变量
# Import Ridge
from sklearn.linear_model import Ridge
alphas = [0.1, 1.0, 10.0, 100.0, 1000.0, 10000.0]
ridge_scores = []
for alpha in alphas:
# Create a Ridge regression model
ridge = Ridge(alpha = alpha)
# Fit the data
ridge.fit(X_train, y_train)
# predict
# y_pred = ridge.predict(X_test)
# Obtain R-squared
score = ridge.score(X_test,y_test)
ridge_scores.append(score)
print(ridge_scores)
Lasso regression
Loss function = OLS loss function +
from sklearn.linear_model import Lasso
scores = []
for alpha in [0.01, 1.0, 10.0, 20.0, 50.0]:
lasso = Lasso(alpha=alpha)
lasso.fit(X_train, y_train)
lasso_pred = lasso.predict(X_test)
scores.append(lasso.score(X_test, y_test))
print(scores)
Lasso regression for feature selection
- Lasso can select important features of a dataset
- Shrinks the coe)cients of less important features to zero
- Features not shrunk to zero are selected by lasso
from sklearn.linear_model import Lasso
X = diabetes_df.drop("glucose", axis=1).values
y = diabetes_df["glucose"].values
names = diabetes_df.drop("glucose", axis=1).columns
lasso = Lasso(alpha=0.1)
lasso_coef = lasso.fit(X, y).coef_
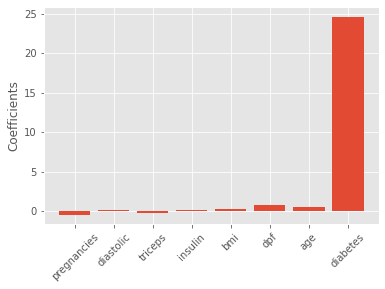
plt.bar(names, lasso_coef)
plt.xticks(rotation=45)
plt.show()