Clustering

The Problem of Clustering

给定一组点，用一个点之间的距离概念，把这些点分成若干个群组，以便

• 一个集群的成员彼此接近/相似
• 不同群组的成员是不一样的

通常情况下，

• 点是在一个高维的空间里
• 相似性的定义是使用距离度量
  • Euclidean, Cosine, Jaccard, edit distance, ...

Example

Clustering Problem: -> Documents

• Represent a document by a vector (x1, x2,..., xd), where x = 1 if the i th word (in some order) appears in the document
• d 是否无限实际上并不重要；即，我们不限制单词集

具有相似词组的文档可能是关于同一主题的

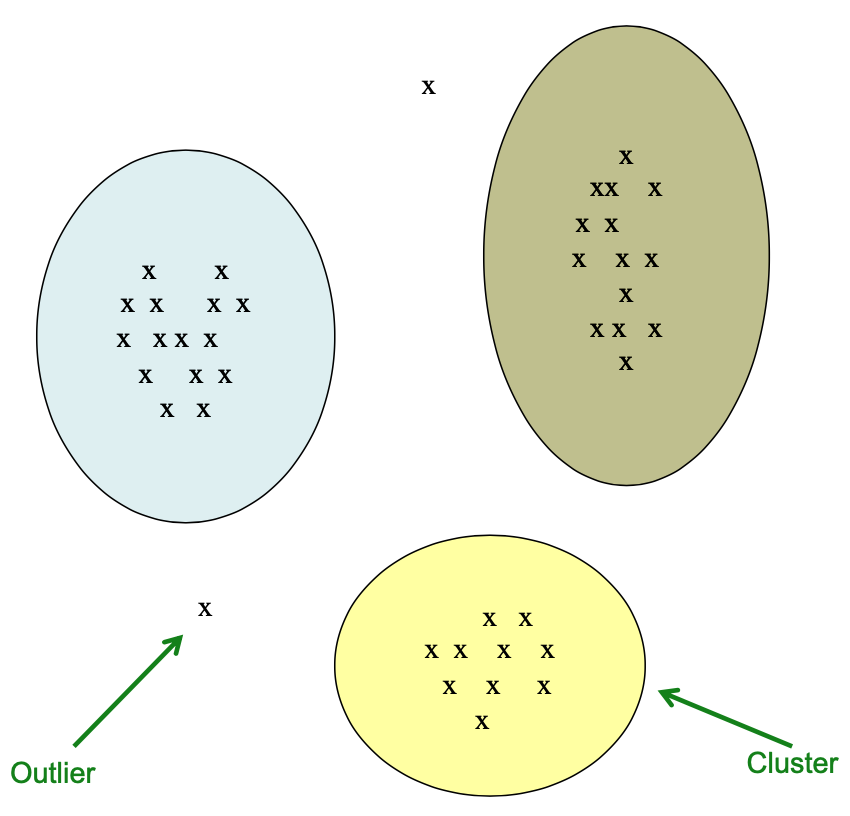
Clusters & Outliers

不可能三角

聚类是一个很难的问题!

• 二维的聚类看起来很容易
• 对少量数据进行聚类看起来很容易
• Many applications involve not 2, but 10 or 10,000 dimensions

高维空间看起来不同：几乎所有成对的点都在差不多的距离上

Distance

Sets as vectors

1.Measure similarity by the cosine distance

$$\text { cosine similarity }=S_{C}(A, B):=\cos (\theta)=\frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\|\|\mathbf{B}\|}=\frac{\sum_{i=1}^{n} A_{i} B_{i}}{\sqrt{\sum_{i=1}^{n} A_{i}^{2}} \sqrt{\sum_{i=1}^{n} B_{i}^{2}}}$$

$$cosine distance = 1 - cosine similarity$$

2.Measure similarity by Euclidean distance

$$d(\mathbf{A}, \mathbf{B})=\sqrt{\sum_{i=1}^{n}\left(B_{i}-A_{i}\right)^{2}}$$

Sets as sets

3.Measure similarity by the Jaccard distance

两个集合的 Jaccard 相似度是它们的交集的大小除以它们的并集的大小：

$$\operatorname{sim}\left(C_{1}, C_{2}\right)=\left|C_{1} \cap C_{2}\right| /\left|C_{1} \cup C_{2}\right|$$

Jaccard distance:

$$d\left(C_{1}, C_{2}\right)=1-\left|C_{1} \cap C_{2}\right| /\left|C_{1} \cup C_{2}\right|$$

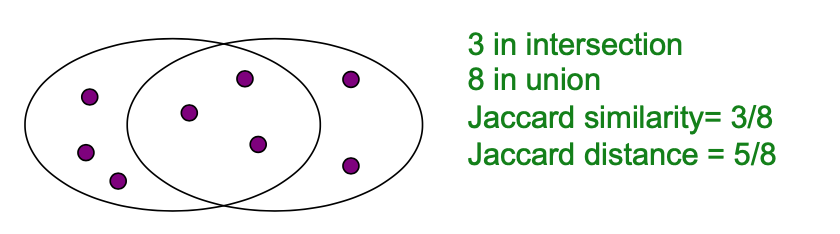
• Document D1 is a set of its 𝑏 words
• 等价地，每个文件是k个词空间中的一个0/1向量
  • Each unique word is a dimension
  • Vectors are very sparse

K-means Clustering

• Assumes Euclidean space/distance
• Start by picking k, the number of clusters, 需要手动指定
• 通过在每个集群中随机选取一个点来初始化集群
  • 示例：随机选择一个点，然后选择 k - 1 个其他点，每个点都尽可能远离之前的点

1677410988187.png

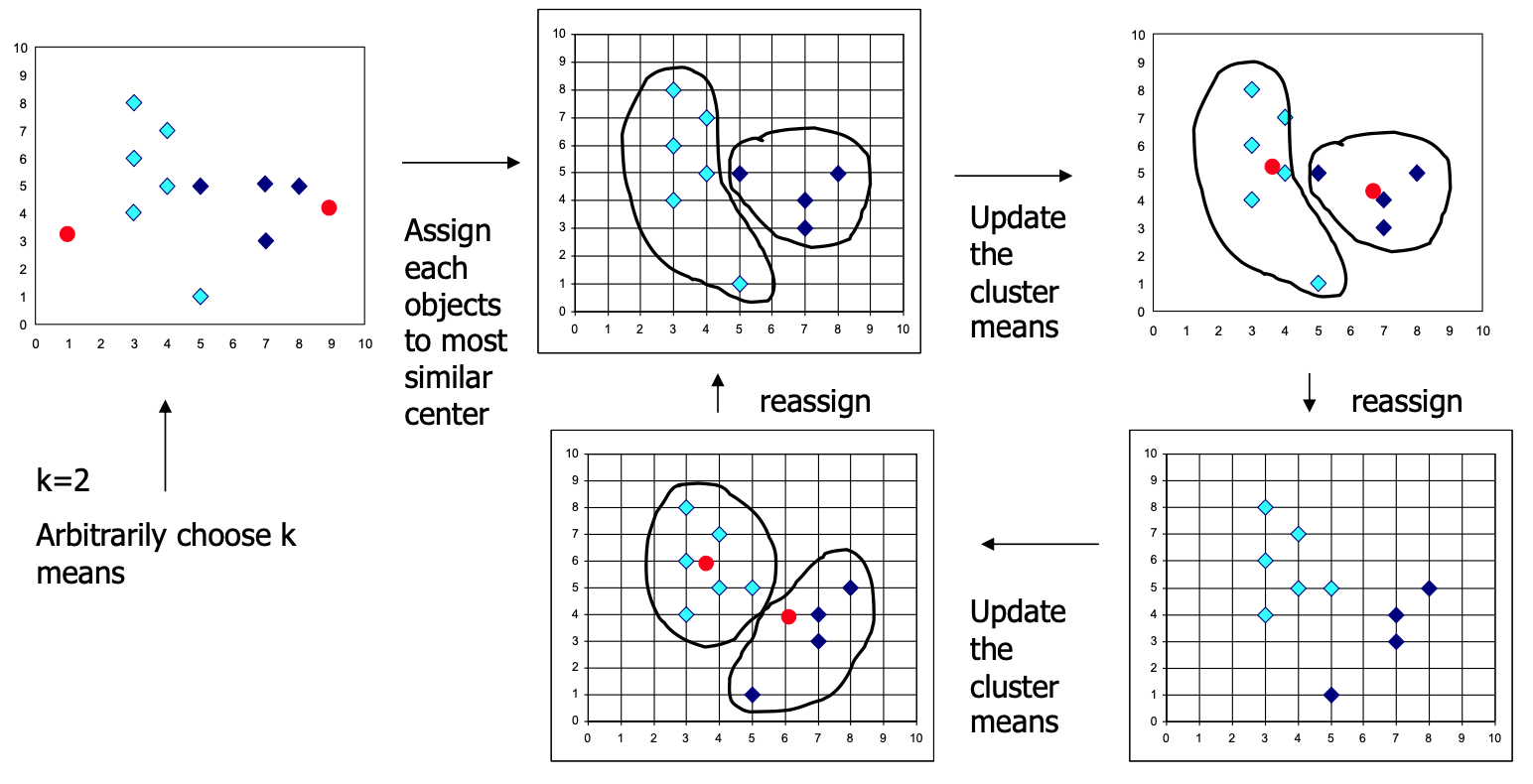
Populating

1. 对于每一个点，将其放在当前中心点最接近的群组中。
2. 在所有的点被分配后，更新 k 个集群的中心点的位置。
3. 将所有的点重新分配到它们最近的中心点上
   • Sometimes moves points between clusters

重复 2 和 3，直到收敛「convergence」

Convergence: Points don’t move between clusters and centroids stabilize

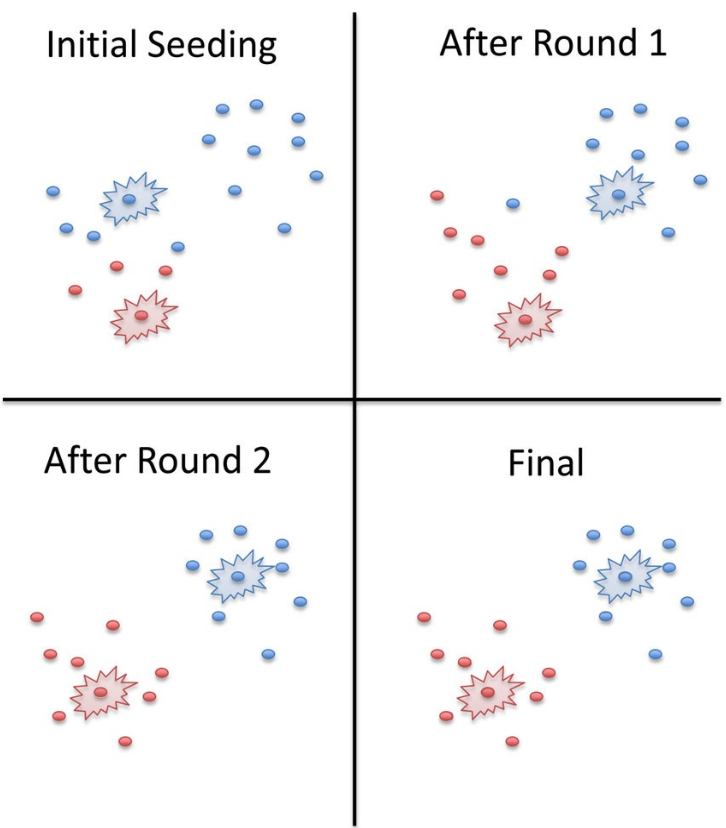
Initialization

• 未指定初始化质心的方法。一种流行的开始方式是随机选择 k 个示例。
• 产生的结果取决于中心点的初始值，而且经常发生发现次优分区的情况。标准的解决方案是尝试一些不同的起点

Pros & Cons

• Simple iterative method
• User provides “K”
• Often too simple ----> bad results
• Difficult to guess the correct “K”：在我们想找到聚类之前，我们可能不知道聚类的数量
• 不保证最佳解决方案

Centroid & Clustroid

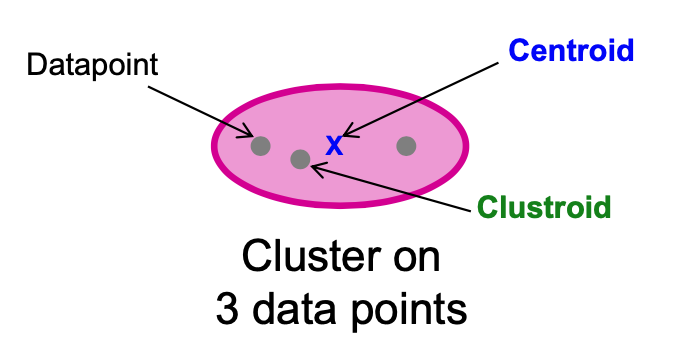
• Centroid 是集群中所有（数据）点的平均值。这意味着中心点是一个 "人工 "点。
• Clustroid 是一个现有的（数据）点，与集群中所有其他点 "最接近"。

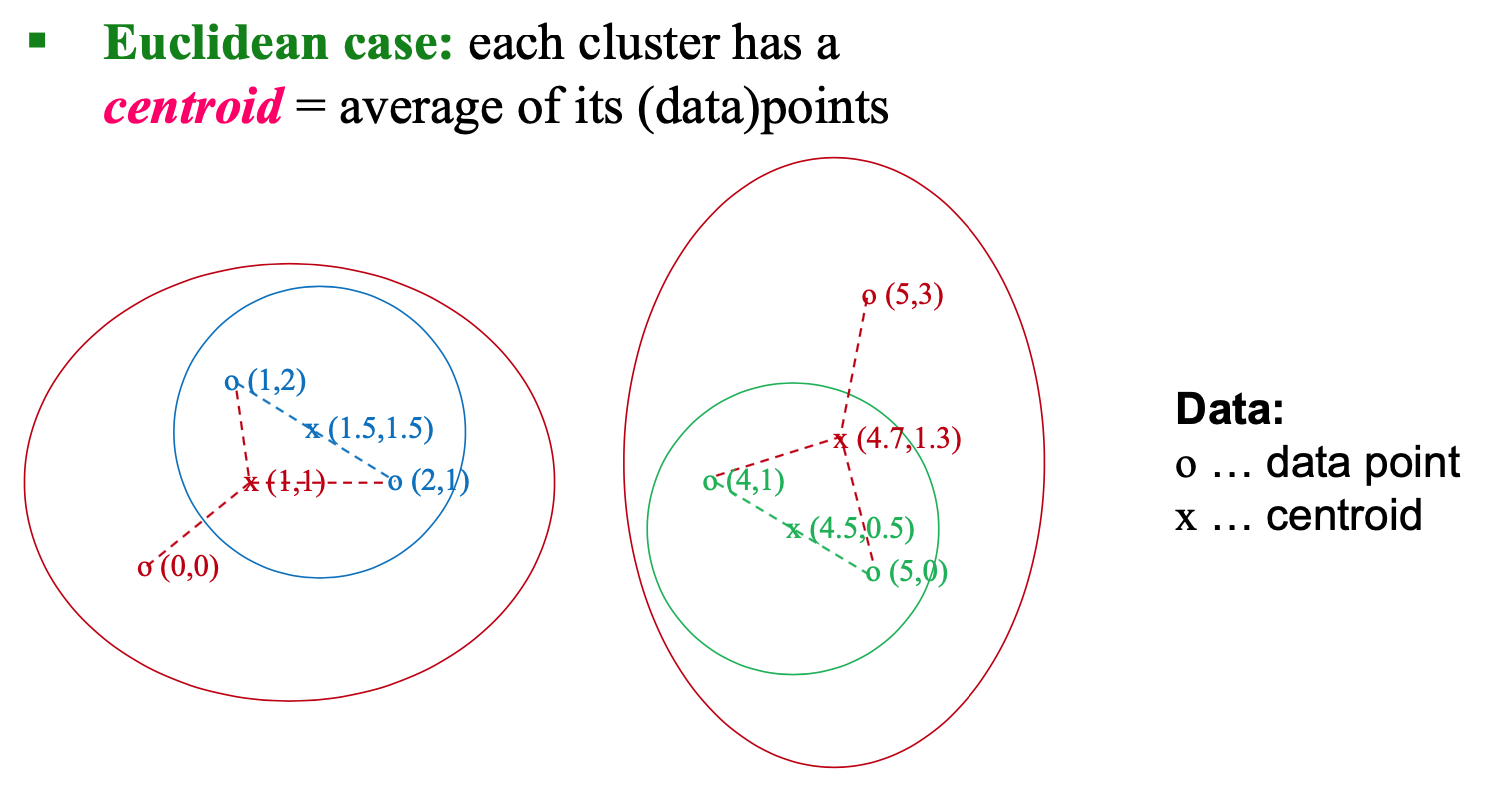
Centroid

1677411669305.png

Clustroid (non-Euclidean Case)

• 我们可以谈论的唯一 "位置 "是点本身，即，没有两个点的 "平均"。
• clustroid = point “closest” to other points
• Possible meanings of “closest”:
  • Smallest average distance to other points
  • Smallest maximum distance to other points
  • Smallest sum of squares of distances to other points, e.g., for distance metric d clustroid c of cluster C is: $\min _{c} \sum_{x \in C} d(x, c)^{2}$