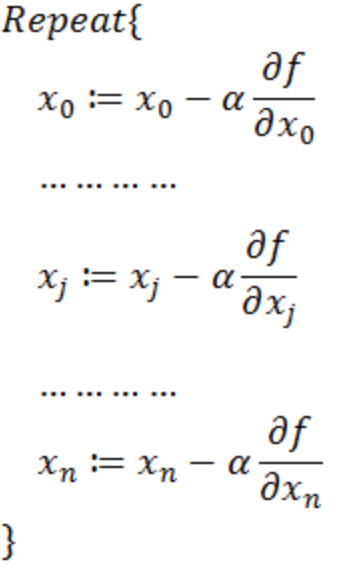梯度下降基础概念

Hirsun大约 19 分钟

梯度下降基础概念

机器学习中的大部分问题都是优化问题，而绝大部分优化问题都可以使用梯度下降法处理。因此相关的基础概念十分重要。

微分/导数

积分「Integral」
微分「Differential」（求积分 = 求导数「Derivative」= 求斜率「Slope」）

f^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}

偏导数

\frac{\partial}{\partial x_{j}} f\left(x_{0}, x_{1}, \ldots, x_{n}\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}, \ldots, x_{j}+\Delta x, \ldots, x_{n}\right)-f\left(x_{0}, \ldots, x_{j}, \ldots, x_{n}\right)}{\Delta x}

提示

$\frac{\partial}{\partial x_{j}}$ 和 $dy/dx$ 一样，只是代表标记。

导数与偏导数本质是一致的，都是当自变量的变化量趋于0时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的变化率。

区别在于：

导数，指的是一元函数中，函数y=f(x)在某一点处沿x轴正方向的变化率；
偏导数，指的是多元函数中，函数 y=f(x1,x2,…,xn )在某一点处沿某一坐标轴（x1,x2,…,xn) 正方向的变化率

方向导数

导数和偏导数的定义，均是沿坐标轴正方向讨论函数的变化率。那么当讨论函数沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一趋近方向上的导数值。

\frac{\partial}{\partial l} f\left(x_{0}, x_{1}, \ldots, x_{n}\right)=\lim _{\rho \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\rho \rightarrow 0} \frac{f\left(x_{0}+\Delta x_{0}, \ldots, x_{j}+\Delta x_{j}, \ldots, x_{n}+\Delta x_{n}\right)-f\left(x_{0}, \ldots, x_{j}, \ldots, x_{n}\right)}{\rho}

\rho=\sqrt{\left(\Delta x_{0}\right)^{2}+\cdots+\left(\Delta x_{j}\right)^{2}+\cdots+\left(\Delta x_{n}\right)^{2}}

通俗的解释是：我们不仅要知道函数在坐标轴正方向上的变化率（即偏导数），而且可能还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。

梯度

\operatorname{gradf}\left(x_{0}, x_{1}, \ldots, x_{n}\right)=\left(\frac{\partial f}{\partial x_{0}}, \ldots, \frac{\partial f}{\partial x_{j}}, \ldots, \frac{\partial f}{\partial x_{n}}\right)

函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。即

梯度是一个向量，即有方向有大小；
梯度的方向是最大方向导数的方向；
梯度的值是最大方向导数的值；

向量理解

偏导数与方向导数是向量吗？

偏导数和方向导数表达的是函数在某一点沿某一方向的变化率，也是具有方向和大小的。

因此从这个角度来理解，我们可以把偏导数和方向导数看作是向量。
向量的方向就是变化率的方向，向量的模是变化率的大小。

那么沿着这样一种思路，就可以如下理解梯度：梯度即函数在某一点最大的方向导数，函数沿梯度方向函数有最大的变化率。

梯度下降法

直观理解

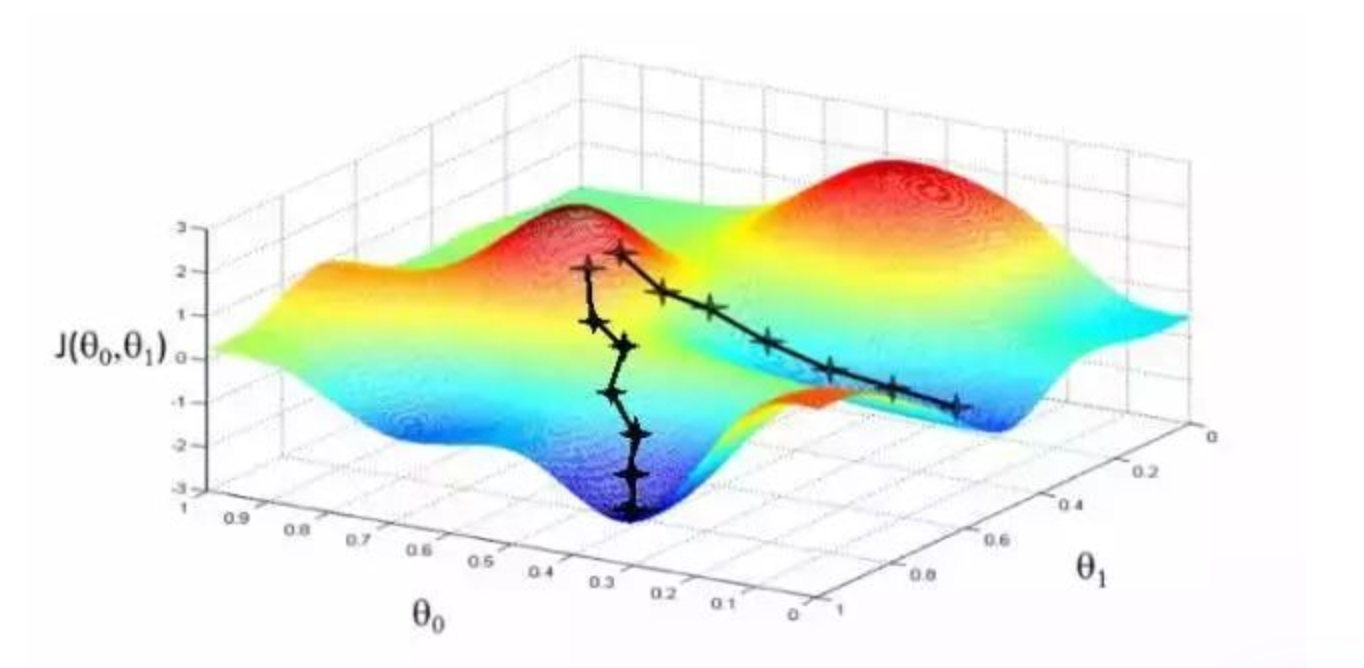
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

做法

既然在变量空间的某一点处，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着负梯度方向去减小函数值，以此达到我们的优化目标。

如何沿着负梯度方向减小函数值呢？梯度和偏导数都是向量，那么参考向量运算法则，我们在每个变量轴上减小对应变量值即可，梯度下降法可以描述如下

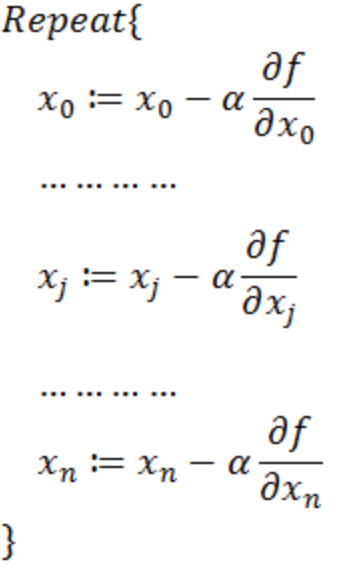
正确性讨论

虽然每次我们将梯度看做向量，但是计算的时候是分方向计算的。

梯度下降法并不是下降最快的方向，它只是目标函数在当前的点的切平面（当然高维问题不能叫平面）上下降最快的方向。

何时停止

If $J\left(\theta_{0}, \theta_{1}\right)$ decreases by less than a threshold 𝜀 (e.g., 10-3) in one iteration

Each iteration, we use all 𝑚 training examples to update $\theta_{0}, \theta_{1}$
Use updated $\theta_{0}, \theta_{1}$ to recalculate $J\left(\theta_{0}, \theta_{1}\right)$ and find the decrease

偏导公式推导

这里关心 $J\left(\theta_{0}, \theta_{1}\right)$ 的偏导数的计算

根据导函数的加法运算法则(f + g)' = f' + g'，也就是多个函数的和的导数等于各函数的导数的和，我们可得到
$\frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m} \frac{\partial}{\partial \theta_{j}}\left(\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}\right)$
又根据复合函数的求导法则f'(g(x)) = f'(u)g'(x)，有
$\begin{aligned} \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right) & =\frac{1}{2 m} \sum_{i=1}^{m} 2\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \\ & =\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \frac{\partial}{\partial \theta_{j}}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right) ......(1) \end{aligned}$
余下部分的偏导就比较简单了，它是对一个二元一次函数的自变量求偏导，根据偏导的定义，对求偏导数时，我们把看作常数，对求偏导数时，我们把看作常数。于是有：
$\frac{\partial}{\partial \theta_{0}}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right)=1$ $\frac{\partial}{\partial \theta_{1}}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right)=x^{(i)}$
把上面两式分别带入（1）式可得：
$\frac{\partial}{\partial \theta_{0}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)$ $\frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x^{(i)}$

梯度下降基础概念

# 梯度下降基础概念

# 微分/导数

# 偏导数

# 方向导数

# 梯度

# 梯度下降法

# 直观理解

# 做法

# 正确性讨论

# 何时停止

# 偏导公式推导

# Ref

梯度下降基础概念

微分/导数

偏导数

方向导数

梯度

梯度下降法

直观理解

做法

正确性讨论

何时停止

偏导公式推导

Ref