机器学习的基本概念

下图展示了机器学习的基本过程。对于学过高中数学的人来说，解方程是我们再熟悉不过的事情了。例如一个二元一次方程组，其解（如果存在的话）就是平面上两条直线的交点，此时方程以及参数（方程的系数）都是确定的。我们通常意义上的算法相当于一个定义好的函数（图1中的h），应用该算法的过程就是带入不同的自变量求函数值的过程。

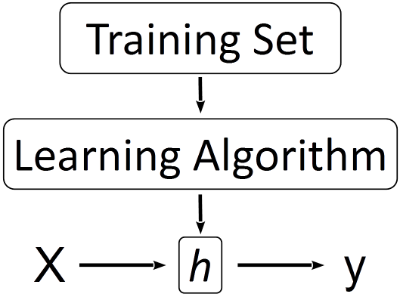
然而在机器学习算法中，最大的不同在于没有一个"定义好的函数"，而是需要通过收集到的数据训练出一个函数（图1中从Training Set到h的过程），本质上是对训练集中数据的一种概括和总结。例如只有两个参数的线性回归就是在二维平面上找一条适合描述训练集中样本点变化规律的直线的过程。

传统的确定性算法与机器学习算法的区别可以用下图表示：

1657295256756.png

如果将一个程序大致分为三个部分：输入、输出和算法，那么传统编程中已知的是输入和算法，需要求输出；机器学习中则是已知输入和输出，需要通过训练（学习）来得到有泛化能力的算法。

• 开普勒通过分析第谷留下的大约20年的天文观测数据，建立的开普勒三大定律；
• 孟德尔通过分析他自己在豌豆实验中获得的不同性状数据，建立了孟德尔遗传定律。

这两位科学家所做的事情，其本质也是对实验数据的概括、总结，最终提炼出了具有高度概括和普适价值的基本定律。这样想想，机器学习算法确实有了几分智能的味道。

一些符号和词汇

训练集（Training Set）

为了研究一个变量（x）与另一个变量（y）的关系，而通过观察、测量等方式获得的一组数据。这组数据中收集了x和与之对应的y，即一个数据对（x, y）。

例如，我们要研究房屋面积（x）和售价（y）之间的关系，每观察一套已出售的房屋，就得到一个数据对（x, y）。观察10套已出售的房屋，就可以得到10个这样的数据对，这时就得到了一个用来研究房屋面积和售价之间的关系的训练集了（虽然样本量比较小）。这些数据集一般采集自现实环境中，属于现象（我们的目的是透过现象看本质）。

样本（Sample）

训练集中一个采集数据的对象就是一个样本，例如 一套已出售的房屋。

模型（Model）

由于某些历史原因，机器学习中的模型也被叫做假设（hypothesis, h），这个 h 就是我们透过现象想要寻找的"本质"。

建立模型的过程通常就是确定一个函数表达式的过程（是否还记得寒假作业中的这类题目：观察一组数，写出下一个数是什么？）。最常见的模型是回归模型（线性回归或逻辑回归等），例如我们假设房屋面积与售价之间的关系是一个线性回归模型，则可以写成：

$$h(\theta)=\theta_{0}+\theta_{1} x$$

• 其中 h 是函数（可能更习惯叫做y，但在机器学习中y一般表示已知的函数值，即后面的因变量
• 这里的h相当于预测得到的y），θ是函数的参数（也可以看做是每个自变量的权重，权重越大，对y的影响也越大）
• x是自变量

训练模型（Training Model）

1. 选定模型（选择合适的模型需要丰富的经验）后，函数的一般形式就确定了。
2. 通常所说的训练模型是指利用训练集求解函数的待定参数的过程。上面的函数式与直线方程的一般形式 y = ax + b 是相同的，这里不过换了一种写法。
   • 此时我们知道模型是一条直线，为了确定这条直线的确定方程，我们需要求出两个未知的参数，即 θ0（截距）和θ1（斜率），如果训练集中只有两个样本，那就只是求一个二元二次方程组就解决问题了。

特征（Feature）

特征就是在一个模型中，所有想研究的自变量（x）的集合。例如我们在研究房屋售价的模型中，所有可能影响售价的因素都可以看成是一个特征，房屋面积、所在城市、房间个数等。

在建立模型的过程中，特征的选择是一个大学问，甚至有专门的分支来研究特征选择或特征表示。

训练集的表示

• 上面提到过，训练集就是许多的（x, y）数据对的集合。
  • 其中x是因变量，y是自变量。
• 通常认为x的变化引起了y的改变，即x的值决定了y的值。
  • 假如我们能找到所有影响房屋价格的因素（所有的x），并且确定各个因素准确的参数（θ），那么理论上可以准确的预测出任何房屋的价格（y）。

训练集中自变量的表示方法

单因素训练集中自变量的表示方法

• 单因素相当于方程中只有一个自变量，这个自变量可以用一个小写字母 x 来表示；
• 如果收集了多个样本，则通过在右上角添加带括号的角标的方式区分，表示为 x⁽¹⁾, x⁽²⁾, ..., x^(m)，其中 m 表示样本的个数；
• 矩阵的表示：向量一般用小写字母表示，矩阵用大写字母表示。所有单因素样本中的x可以用一个 m x 1（m行1列）的列向量x(小写字母)（只有一列的矩阵就是一个列向量）来表示：

$$x=\left(\begin{array}{c} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(m)} \end{array}\right)$$

多因素训练集中自变量的表示方法

• 多因素相当于方程中有多个自变量（多个feature），不同的自变量之间使用右下角添加不带括号的角标来区分，表示为x1, x2, ..., xn，其中n表示feature的个数；
• 当存在多个样本时，可以用一个m x n（m行n列）的矩阵X(大写字母)来表示：

$$X=\left[\begin{array}{cccc} x_{1}^{(1)} & x_{2}^{(1)} & \cdots & x_{n}^{(1)} \\ x_{1}^{(2)} & x_{2}^{(2)} & \cdots & x_{n}^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_{1}^{(m)} & x_{2}^{(m)} & \cdots & x_{n}^{(m)} \end{array}\right]$$

训练集中因变量的表示方法

无论是单因素还是多因素，每一个样本中都只包含一个因变量（y），因此只需要区分不同样本间的y，y(1), y(2), ..., y(m)，其中m表示样本的个数；用列向量y表示为：

$$y=\left(\begin{array}{c} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{array}\right)$$

模型的表示

这里说的模型就是一个特定的函数，上面已经提过，模型一般使用h来表示。下面用线性回归模型来举例说明模型的符号表示。

直接表示

直接表示方法是我们在没有学习线性代数之前的代数表示方式。

• 单变量线性回归方程: $h_{\theta}(x)=\theta_{0}+\theta_{1} x$
• 多变量线性回归方程: $h_{\theta}(x) = \theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\theta_{3} x_{3}+\ldots+\theta_{n} x_{n}$

矩阵表示

学习了线性代数后，可以使用矩阵来表示上面的方程，不仅表示起来方便，直接进行矩阵运算效率也更高效。

在这里需要特别说明的一点是，为了配合矩阵的表示，在上面的方程中添加了x₀，并且x₀=1，且将θ₀作为x₀的参数。

$$h_{\theta}(x)=X \theta=\left[\begin{array}{cccc} x_{0}^{(1)} & x_{1}^{(1)} & \cdots & x_{n}^{(1)} \\ x_{0}^{(2)} & x_{1}^{(2)} & \cdots & x_{n}^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_{0}^{(m)} & x_{1}^{(m)} & \ldots & x_{n}^{(m)} \end{array}\right]\left[\begin{array}{c} \theta_{0} \\ \theta_{1} \\ \vdots \\ \theta_{n} \end{array}\right]$$

此时 X 是一个 m x (n+1) 的矩阵

• 每一行表示同一个样本，共有m个样本，写到上标
• 每一列表示同一个特征，共有n个特征，写到下标
• 其中m表示样本的个数，n表示变量的个数

当只有一个样本多个变量时，表示为：

$$h_{\theta}(x)=\theta^{T} x=\left[\begin{array}{llll} \theta_{0} & \theta_{1} & \ldots & \theta_{n} \end{array}\right]\left[\begin{array}{c} x_{0} \\ x_{1} \\ \vdots \\ x_{n} \end{array}\right]$$

Reference

• https://www.coursera.org/learn/machine-learning
• http://blog.sciencenet.cn/blog-100379-1037923.html
• https://www.sumologic.com/blog/devops/machine-learning-deep-learning/
• https://www.cnblogs.com/Belter/p/6323390.html