多项式回归模型
大约 6 分钟
多项式回归模型
在上一篇的一般线性回归中,使用的假设函数是一元一次方程,也就是二维平面上的一条直线。但是很多时候可能会遇到直线方程无法很好的拟合数据的情况,这个时候可以尝试使用多项式回归。
多项式回归中,加入了特征的更高次方(例如平方项或立方项),也相当于增加了模型的自由度,用来捕获数据中非线性的变化。
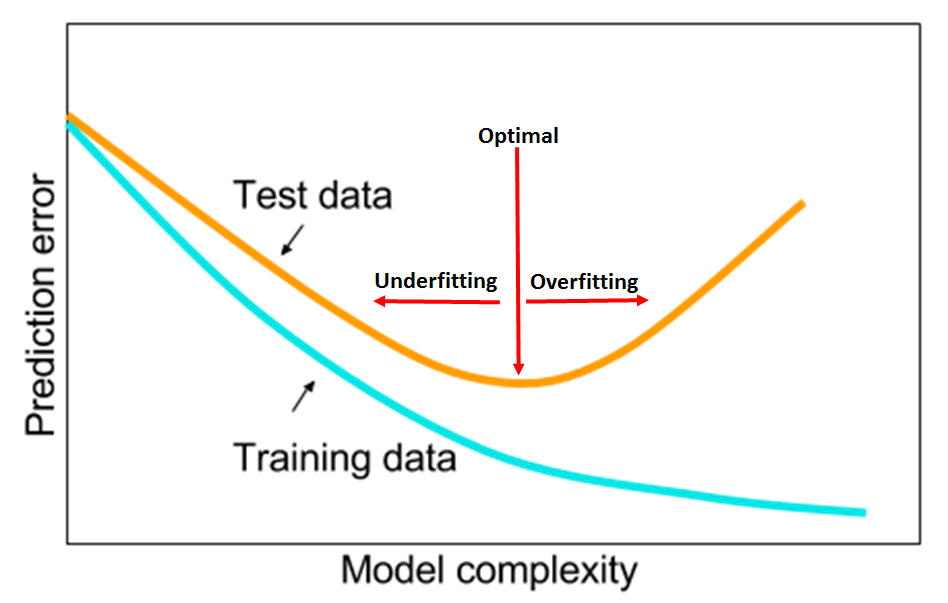
添加高阶项的时候,也增加了模型的复杂度。随着模型复杂度的升高,模型的容量以及拟合数据的能力增加,可以进一步降低训练误差,但导致过拟合的风险也随之增加。下图展示了模型复杂度与训练误差及测试误差之间的关系
一般形式
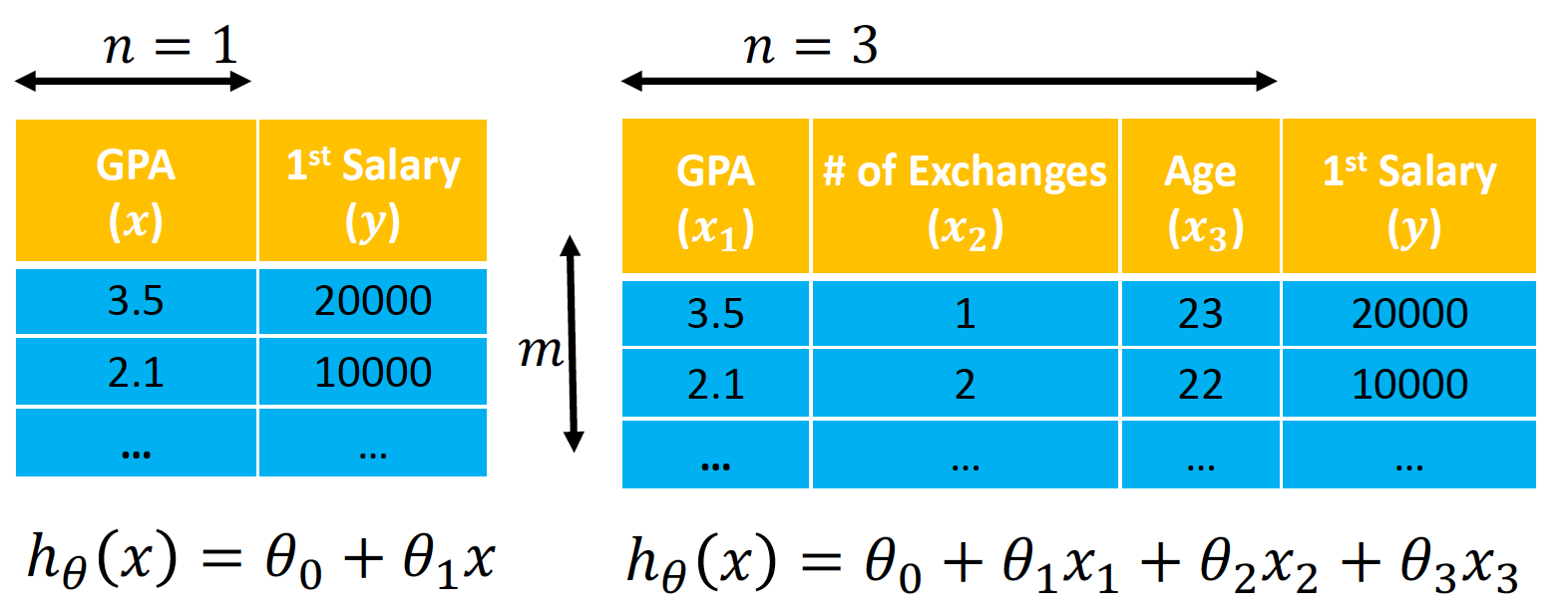
在多项式回归中,最重要的参数是最高次方的次数。设最高次方的次数为n,且只有一个特征时,其多项式回归的方程为:
如果令x0=1,在多样本的情况下,可以写成向量化的形式: ,其中
- X是大小为 m⋅(n+1) 的矩阵
- θ 是大小为 (n+1)⋅1 的矩阵。
在这里虽然只有一个特征x以及x的不同次方,但是也可以将x的高次方当做一个新特征。与多元回归分析唯一不同的是,这些特征之间是高度相关的,而不是通常要求的那样是相互对立的。
看待问题的角度不同,得到的结果也不同。我们就认为多项式回归仍然是参数的线性模型。
代价函数
- 更新梯度
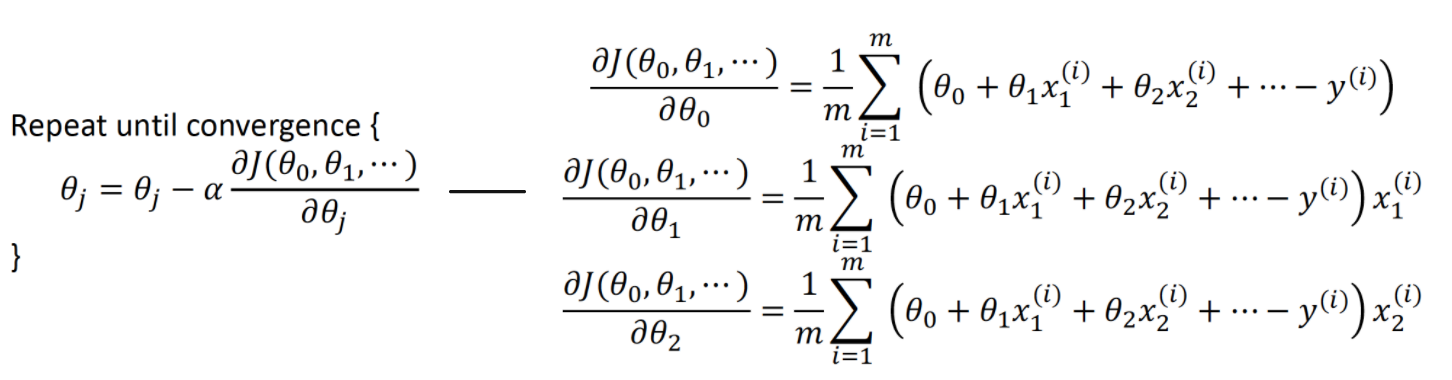
- n = n +1
直到 或者 结束。