线性回归模型 线性回归应该是我们听过次数最多的机器学习算法了。在一般的统计学教科书中,最后都会提到这种方法。因此该算法也算是架起了数理统计与机器学习之间的桥梁。
线性回归虽然常见,但是却并不简单。该算法中几乎包含了所有有监督机器学习算法的重要知识点,比如数据的表示、参数的训练、模型的评价、利用正则化防止过拟合等概念。
线性回归模型最小化点与超平面(单个特征的线)之间的距离。 所以说如果掌握了线性回归,可以为后面的学习打下坚实的基础。
基本形式 最简单的线性回归就是直接利用一条直线拟合二维平面上的一系列点,目的是利用这条直线概括所有训练集中样本的散布规律或趋势,最终用于新样本点的预测。
二维平面上直线方程的一般形式为 y = a x + b y=a x+b y = a x + b i ,就可以带入上面学习到的公式计算y的值了。
在三维空间中,需要学习的是确定一个二维平面的参数;以此类推,在n维空间中,需要学习的是确定一个n−1维的超平面的参数。之所以称该方法为线性模型,是因为该模型是由所有特征的线性组合构成 的,基本形式为:
y ^ = h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n ⋯ ( 1 − 1 ) \hat{y}=h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} \quad \cdots(1-1) y ^ = h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n ⋯ ( 1 − 1 )
y^表示线性回归模型的预测值(相对于真实观察值); n表示特征的数量; xi表示第i个特征的观察值; θj表示第j个参数的值. 如果模型包括n个特征,那么就会包括 n+1个参数,还包括常数项(还被称为截距)。
式子(1-1)使用向量化形式可以表示为 h θ = θ T x h_{\theta}=\theta^{T} x h θ = θ T x
代价函数 对于线性回归算法,比较常用的代价函数是均方误差(Mean Square Error, MSE)函数:
J ( θ ) = M S E ( X , h θ ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( θ T ⋅ x ( i ) − y ( i ) ) 2 ⋯ ( 2 − 1 ) J(\theta)=M S E\left(X, h_{\theta}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}^{(i)}-y^{(i)}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(\theta^{T} \cdot x^{(i)}-y^{(i)}\right)^{2} \quad \cdots(2-1) J ( θ ) = MSE ( X , h θ ) = 2 m 1 i = 1 ∑ m ( y ^ ( i ) − y ( i ) ) 2 = 2 m 1 i = 1 ∑ m ( θ T ⋅ x ( i ) − y ( i ) ) 2 ⋯ ( 2 − 1 )
上式表示所有模型的预测值与实际观察值之差的平方和,因此训练集中任何一个实际观察值与模型预测值之间的误差都包含在了这个公式中; 为了求导方便,添加了一个系数1/2,实际的MSE的定义中是没有的; 该函数是一个凸函数. 利用正规方程求解 先看一下正规方程的定义:
最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程.
就像利用 “一阶导数等于0的点是极值点” 的性质,可以非常容易求出一元二次方程的极值点一样,我们也可以采用代数的方法直接计算式子 (2-1) 的最小值点。实际上经过计算可以得到:
θ = ( X T X ) − 1 X T y \theta=\left(X^{T} X\right)^{-1} X^{T} y θ = ( X T X ) − 1 X T y
也就是说,不用经过训练就可以直接利用上面的公式计算出线性回归模型的最优解。既然有了这么方便的方法,为什么我们还需要其他的训练方法(例如梯度下降)呢?这是因为求一个矩阵的逆运算量非常大,例如求一个 n⋅n 的矩阵的逆,其计算复杂度为O(n3 )。因此,在样本量非常大时利用梯度下降来训练模型所消耗的时间远远小于直接使用正规方程计算结果所消耗的时间。当然,在样本量非常小的情况下,利用该方法还是非常方便的。
利用梯度下降训练模型 梯度下降几乎可以说是机器学习算法中,训练模型和调参最重要的方法了。梯度就是所有偏导数构成的向量。因为计算代价函数的梯度需要求导,这里应该是机器学习中使用微积分最多的地方了。
梯度算法的核心是反复迭代改变和的值直到代价函数J的值达到最小,这里关键是如何去求J的偏导数。
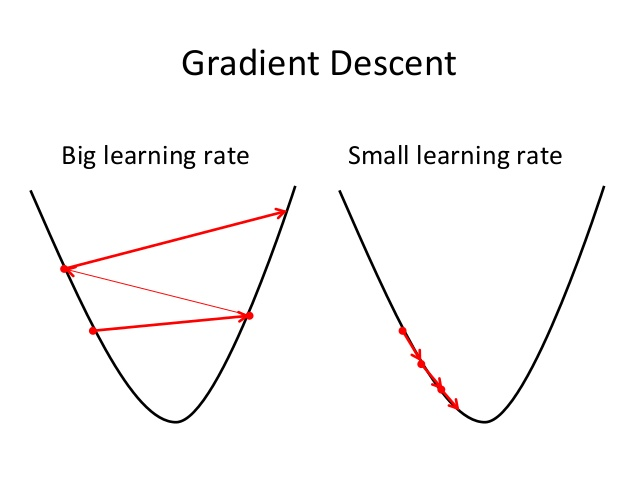
梯度下降的一般步骤 参数的初始化:通常所有参数都初始化为1或者0; 确定学习率; 求代价函数的梯度(所有参数的偏导数); 所有参数都沿梯度方向移动一步,步长就是学习率a的大小;这是用户指定的一个常数。 重复步骤4直到参数不再发生变化(此时取到极值点,梯度为0),或达到预先设定的迭代次数. 学习率 学习率一般用希腊字母 α 表示,可能需要多尝试几次,才能找到合适的学习率。
过大的学习率会导致梯度下降时越过代价函数的最小值点,随着训练步数的增加,代价函数不减反增; 如果学习率太小,训练中的每一步参数的变化会非常小,这时可以看到代价函数的值在不断减小,但是需要非常大的迭代次数才能到达代价函数的最小值点。 按照吴恩达老师的建议,每次可以3倍放大或者3倍缩小来调整,直到找到合适的学习率。
代价函数的梯度 为了简单起见,先考虑只有一个特征的直线方程:
h ( θ ) = θ 0 + θ 1 x 1 h_{(\theta)}=\theta_{0}+\theta_{1} x_{1} h ( θ ) = θ 0 + θ 1 x 1
令 x0 =1,则可得 h ( θ ) = θ 0 x 0 + θ 1 x 1 h_{(\theta)}=\theta_{0} x_{0}+\theta_{1} x_{1} h ( θ ) = θ 0 x 0 + θ 1 x 1
每个参数都有一个偏导数 ,且综合了所有样本的信息。参考MSE的公式,见式子(2-1),可得,
J ( θ ) J(\theta) J ( θ ) θ 0 \theta_{0} θ 0 ∂ ∂ θ 0 J ( θ ) = 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) ] ⋯ ( 3 − 1 ) \frac{\partial}{\partial \theta_{0}} J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left[\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{0}^{(i)}\right] \quad \cdots(3-1) ∂ θ 0 ∂ J ( θ ) = m 1 ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) ] ⋯ ( 3 − 1 )
J ( θ ) J(\theta) J ( θ ) θ 1 \theta_{1} θ 1 ∂ ∂ θ 1 J ( θ ) = 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) ] ⋯ ( 3 − 2 ) \frac{\partial}{\partial \theta_{1}} J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left[\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{1}^{(i)}\right] \quad \cdots(3-2) ∂ θ 1 ∂ J ( θ ) = m 1 ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) ] ⋯ ( 3 − 2 )
其中
m表示样本数量; y ( i ) y^{(i)} y ( i ) x 1 i x_{1}^{i} x 1 i 式子中的点号⋅表示普通乘法 梯度
在该案例中,
J ( θ 0 , θ 1 ) J\left(\theta_{0}, \theta_{1}\right) J ( θ 0 , θ 1 ) 偏导数 「partial derivative」∂ J ( θ 0 , θ 1 ) ∂ θ j \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{j}} ∂ θ j ∂ J ( θ 0 , θ 1 ) J ( θ 0 , θ 1 ) J\left(\theta_{0}, \theta_{1}\right) J ( θ 0 , θ 1 ) θ j \theta_{j} θ j Gradient of 𝐽 is the vector is ∇ J ( θ 0 , θ 1 ) = [ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] \nabla J\left(\theta_{0}, \theta_{1}\right)=\left[\begin{array}{l} \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{0}} \\ \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{1}} \end{array}\right] ∇ J ( θ 0 , θ 1 ) = [ ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ∂ J ( θ 0 , θ 1 ) ] (3-1) 和 (3-2) 化简之后分别是
∂ J ( θ 0 , θ 1 ) ∂ θ 0 = 1 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{0}}=\frac{1}{m} \sum_{i=1}^{m}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) = m 1 i = 1 ∑ m ( θ 0 + θ 1 x ( i ) − y ( i ) )
∂ J ( θ 0 , θ 1 ) ∂ θ 1 = 1 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) x ( i ) \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{1}}=\frac{1}{m} \sum_{i=1}^{m}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right) x^{(i)} ∂ θ 1 ∂ J ( θ 0 , θ 1 ) = m 1 i = 1 ∑ m ( θ 0 + θ 1 x ( i ) − y ( i ) ) x ( i )
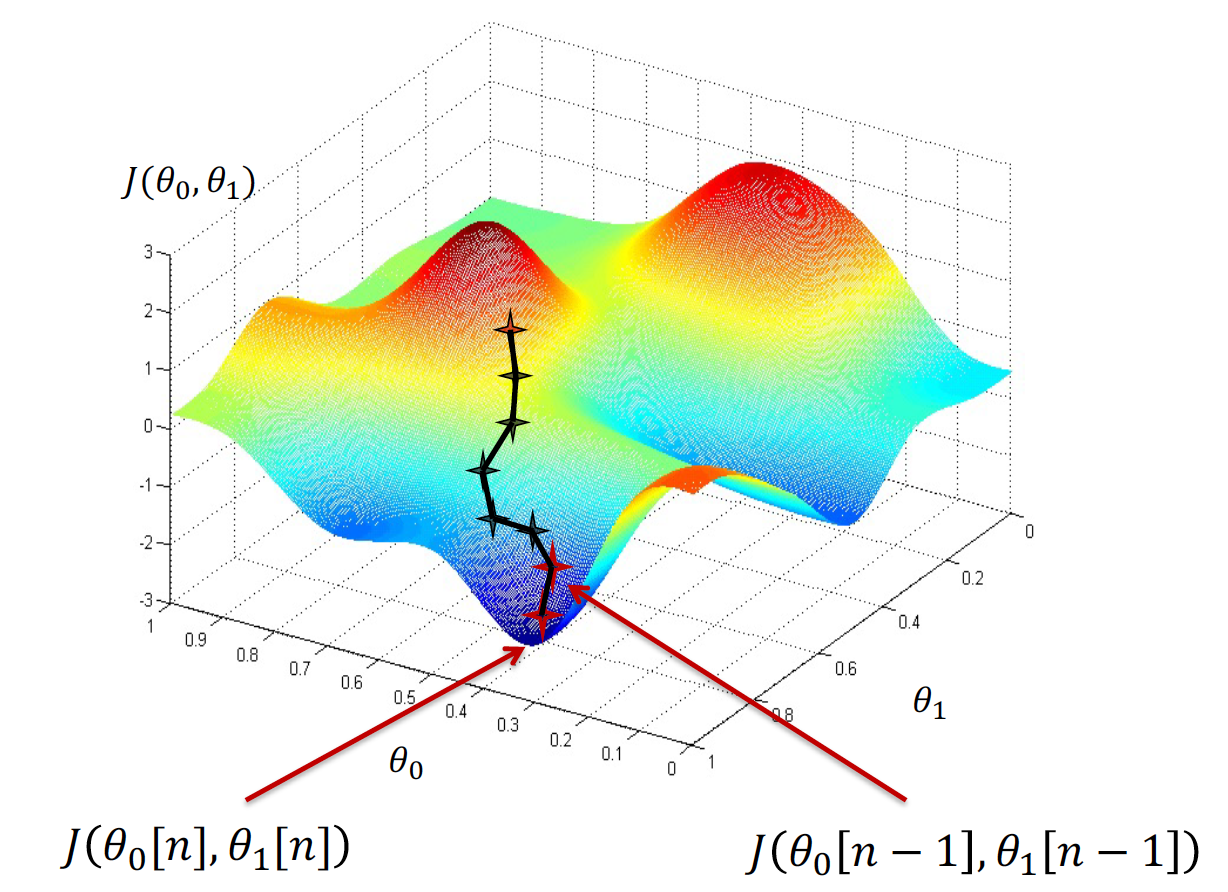
具体的过程 Input: ( x ( 1 ) , y ( 1 ) ) , … , ( x ( m ) , y ( m ) ) \left(x^{(1)}, y^{(1)}\right), \ldots,\left(x^{(m)}, y^{(m)}\right) ( x ( 1 ) , y ( 1 ) ) , … , ( x ( m ) , y ( m ) ) Start with some θ0 , θ1 (e.g. θ0 = 0, θ1 = 0) 继续计算 θ0 , θ1 直到他们达到我们希望以内的最小值 具体过程是
初始化 n = 0 , θ 0 [ n ] = 0 , θ 1 [ n ] = 0 n=0, \theta_{0}[n]= 0,\theta_{1}[n]=0 n = 0 , θ 0 [ n ] = 0 , θ 1 [ n ] = 0
对以下过程 1 -> 2 -> 3 不断循环
J ( θ 0 , θ 1 , ⋯ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left(\theta_{0}, \theta_{1}, \cdots\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J ( θ 0 , θ 1 , ⋯ ) = 2 m 1 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 θ j = θ j − α ∂ J ( θ 0 , θ 1 ) ∂ θ j \theta_{j}=\theta_{j}-\alpha \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{j}} θ j = θ j − α ∂ θ j ∂ J ( θ 0 , θ 1 ) θ 0 = θ 0 − α ⋅ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 \theta_{0}=\theta_{0}-\alpha \cdot \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{0}} θ 0 = θ 0 − α ⋅ ∂ θ 0 ∂ J ( θ 0 , θ 1 ) θ 1 = θ 1 − α ⋅ ∂ J ( θ 0 , θ 1 ) ∂ θ 1 \theta_{1}=\theta_{1}-\alpha \cdot \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{1}} θ 1 = θ 1 − α ⋅ ∂ θ 1 ∂ J ( θ 0 , θ 1 ) n = n +1 直到 J ( θ 0 [ n − 1 ] , θ 1 [ n − 1 ] ) − J ( θ 0 [ n ] , θ 1 [ n ] ) < ε J\left(\theta_{0}[n-1], \theta_{1}[n-1]\right)-J\left(\theta_{0}[n], \theta_{1}[n]\right)<\varepsilon J ( θ 0 [ n − 1 ] , θ 1 [ n − 1 ] ) − J ( θ 0 [ n ] , θ 1 [ n ] ) < ε n > X n>X n > X
使用scikit-learn工具包 自己实现算法是学习算法最好的方式,当我们掌握了这类算法的基本原理,就不用每次都自己实现了。因为这些算法都是非常成熟的机器学习算法,有许多程序包都实现了这些算法。
在Python中,使用比较广泛的是scikit-learnopen in new window 这个工具包,这个package最开始由google的暑期实习生David Cournapeau开发,第一个版本公开于2010年2月。现在是Python社区中开发活跃且广泛使用的开源机器学习工具。
sk-learn模型为我们做了下面这些事情:
参数的初始化; 选择学习率; 求代价函数的梯度; 参数的更新. 我们也不需要对输入的训练集做任何处理(例如前面的方法都需要为每一个样本点添加x0=1),只需要选择算法并且输入带标签(y)的训练集(X)就可以了。
模型训练完成后,截距(θ0)的值保存在intercept_中,其他参数保存在coef_中。
Reference