Cost Function

Hirsun，Belter大约 28 分钟

Cost Function

假设现在有了训练数据和模型，那么要怎么开始训练呢？这时候就必须定义一个代价函数，代价函数量化了模型预测值与实际观察值之间的误差大小。有了代价函数就可以评价取当前参数时模型性能的好坏。

代价函数（有的地方也叫损失函数，Loss Function）在机器学习中的每一种算法中都很重要。因为训练模型的过程就是优化代价函数的过程，代价函数对每个参数的偏导数就是梯度下降中提到的梯度。防止过拟合时添加的正则化项也是加在代价函数后面。

成本函数的值不等同于预测误差。

什么是代价函数

假设有训练样本(x, y)，模型为h，参数为θ。h(θ) = θ^Tx（θ^T表示θ的转置）

概况来讲，任何能够衡量模型预测出来的值h(θ)与真实值y之间的差异的函数都可以叫做代价函数C(θ)，如果有多个样本，则可以将所有代价函数的取值求均值，记做J(θ)。

因此很容易就可以得出以下关于代价函数的性质：

对于每种算法来说，代价函数不是唯一的；
代价函数是参数θ的函数；
总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；
J(θ)是一个标量；

当我们确定了模型h，后面做的所有事情就是训练模型的参数θ。那么什么时候模型的训练才能结束呢？

由于代价函数是用来衡量模型好坏的，我们的目标当然是得到最好的模型（也就是最符合训练样本(x, y)的模型）。因此训练参数的过程就是不断改变θ，从而得到更小的J(θ)的过程。理想情况下，当我们取到代价函数J的最小值时，就得到了最优的参数θ，记为： $\min _{\theta} J(\theta)$

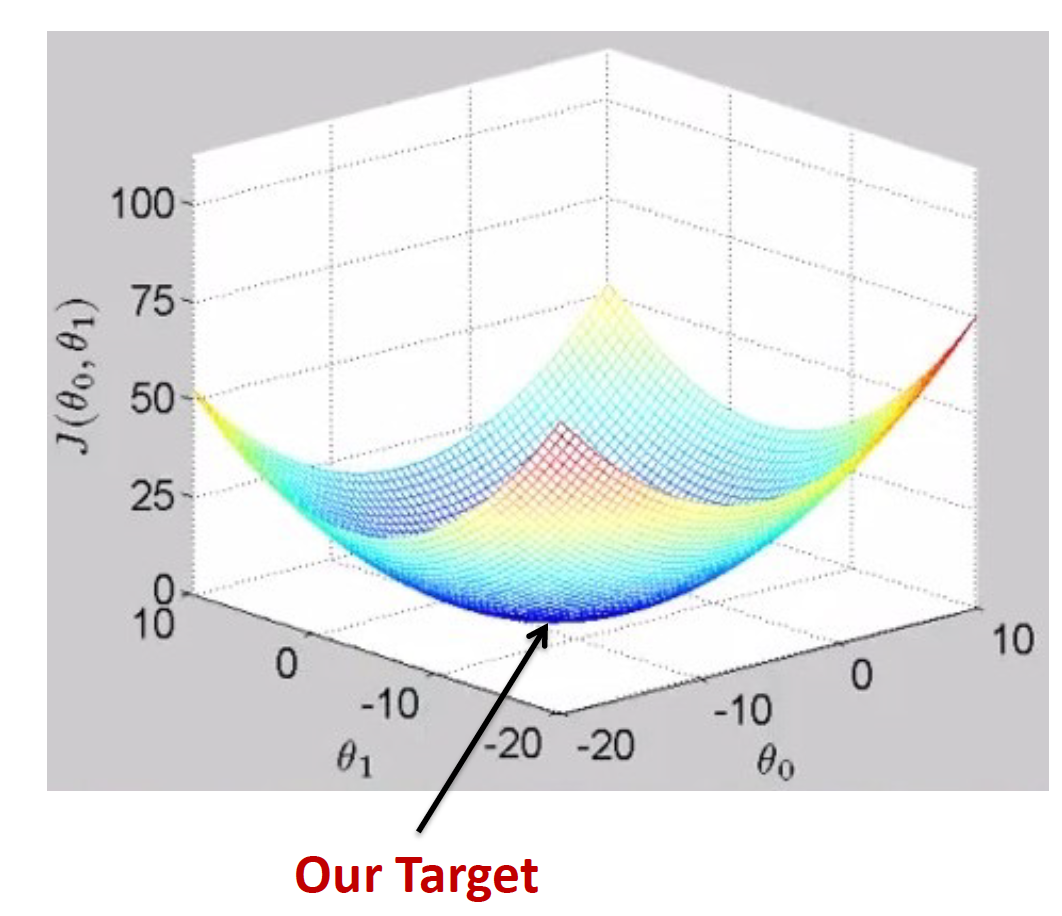
例如，J(θ) = 0，表示我们的模型完美的拟合了观察的数据，没有任何误差。

在优化参数θ的过程中，最常用的方法是梯度下降，这里的梯度就是代价函数J(θ)对θ1, θ2, ..., θn的偏导数。由于需要求偏导，我们可以得到另一个关于代价函数的性质：

选择代价函数时，最好挑选对参数θ可微的函数（全微分存在，偏导数一定存在）

在选择一个恰当的代价函数后，整个模型的训练过程就是求代价函数最小值的过程。这个过程并不容易，可能会出现下面两种情况：

得到全局最优解：即代价函数的最小值；
得到局部最优解：由于很多原因我们可能仅仅只能求的代价函数在某个区间内的极小值.

如果代价函数是一个凸函数（convex function），那么从数学上可以保证肯定能求得全局最优解；如果代价函数是非凸函数，就无法从理论上保证最终能得到代价函数的全局最优解（NP-hard问题）。

代价函数的常见形式

经过上面的描述，一个好的代价函数需要满足两个最基本的要求：

能够评价模型的准确性
对参数θ可微。

均方误差

在线性回归中，最常用的是均方误差(Mean squared error)，具体形式为：

J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}^{(i)}-y^{(i)}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}

训练样本的个数；
h_θ(x)：用参数θ和x预测出来的y值；
y：原训练样本中的y值，也就是标准答案
上角标(i)：第i个样本

为什么是1/2m 而不是 1/m ?

在吴恩达机器学习视频公开课上的讲解是为了其他数学计算的方便。其实无论是除以m 还是除以2m，代价函数的最优解都是相同的。

数学计算的方便：之后利用梯度下降法对J求导，如果是2m，求导结果为

\frac{\partial J}{\partial \theta_{i}}=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \frac{\partial h_{\theta}\left(x^{(i)}\right)}{\partial \theta}

这里正好除以m，便于计算。

交叉熵

在逻辑回归中，最常用的是代价函数是交叉熵(Cross Entropy)，交叉熵是一个常见的代价函数，在神经网络中也会用到。下面是《神经网络与深度学习》一书对交叉熵的解释：

交叉熵是对「出乎意料」（译者注：原文使用suprise）的度量。神经元的目标是去计算函数y, 且y=y(x)。但是我们让它取而代之计算函数a, 且a=a(x)。假设我们把a当作y等于1的概率，1−a是y等于0的概率。那么，交叉熵衡量的是我们在知道y的真实值时的平均「出乎意料」程度。当输出是我们期望的值，我们的「出乎意料」程度比较低；当输出不是我们期望的，我们的「出乎意料」程度就比较高。

一个事件的香农信息量等于0，表示该事件的发生不会给我们提供任何新的信息，例如确定性的事件，发生的概率是1，发生了也不会引起任何惊讶；当不可能事件发生时，香农信息量为无穷大，这表示给我们提供了无穷多的新信息，并且使我们无限的惊讶。代价函数的公式为

J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m}\left(y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]\right.

符号说明同上

神经网络中的代价函数

学习过神经网络后，发现逻辑回归其实是神经网络的一种特例（没有隐藏层的神经网络）。因此神经网络中的代价函数与逻辑回归中的代价函数非常相似：

J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{K}\left(y_{k}^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\theta}\left(x^{(i)}\right)\right)_{k}\right)\right]\right.

这里之所以多了一层求和项，是因为神经网络的输出一般都不是单一的值，K表示在多分类中的类型数。

查看案例

例如在数字识别中，K=10，表示分了10类。此时对于某一个样本来说，输出的结果如下：

 1.1266e-004
  1.7413e-003
  2.5270e-003
  1.8403e-005
  9.3626e-003
  3.9927e-003
  5.5152e-003
  4.0147e-004
  6.4807e-003
  9.9573e-001

一个10维的列向量，预测的结果表示输入的数字是0~9中的某一个的概率，概率最大的就被当做是预测结果。例如上面的预测结果是9。理想情况下的预测结果应该如下（9的概率是1，其他都是0）：

比较预测结果和理想情况下的结果，可以看到这两个向量的对应元素之间都存在差异，共有10组，这里的10就表示代价函数里的K，相当于把每一种类型的差异都累加起来了。

代价函数与参数

函数衡量的是模型预测值h(θ) 与标准答案y之间的差异，所以总的代价函数J是h(θ)和y的函数，即J=f(h(θ), y)。
又因为y都是训练样本中给定的，h(θ)由θ决定，所以，最终还是模型参数θ的改变导致了J的改变。

对于不同的θ，对应不同的预测值h(θ)，也就对应着不同的代价函数J的取值。变化过程为：θ −−> h(θ) −−> J(θ)

θ引起了h(θ)的改变，进而改变了J(θ)的取值。为了更直观的看到参数对代价函数的影响，举个简单的例子：

有训练样本{(0, 0), (1, 1), (2, 2), (4, 4)}，即4对训练样本，每个样本对中第1个数表示x的值，第2个数表示y的值。这几个点很明显都是y=x这条直线上的点。如下图, 不同参数可以拟合出不同的直线

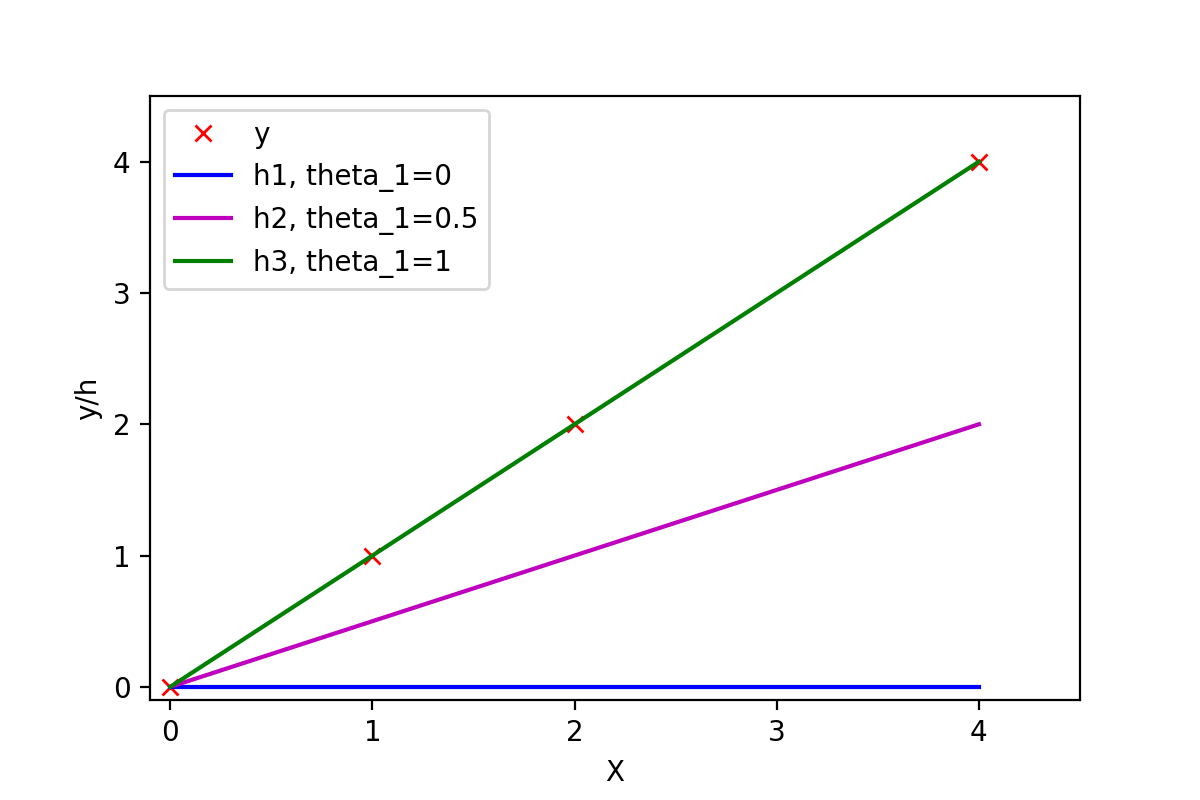
常数项为0，所以可以取θ0=0，然后取不同的θ1，可以得到不同的拟合直线。

当θ1=0时，拟合的直线是y=0，即蓝色线段，此时距离样本点最远，代价函数的值（误差）也最大；
当θ1=1时，拟合的直线是y=x，即绿色线段，此时拟合的直线经过每一个样本点，代价函数的值为0。

通过下图可以查看随着θ1的变化，J(θ)的变化情况：

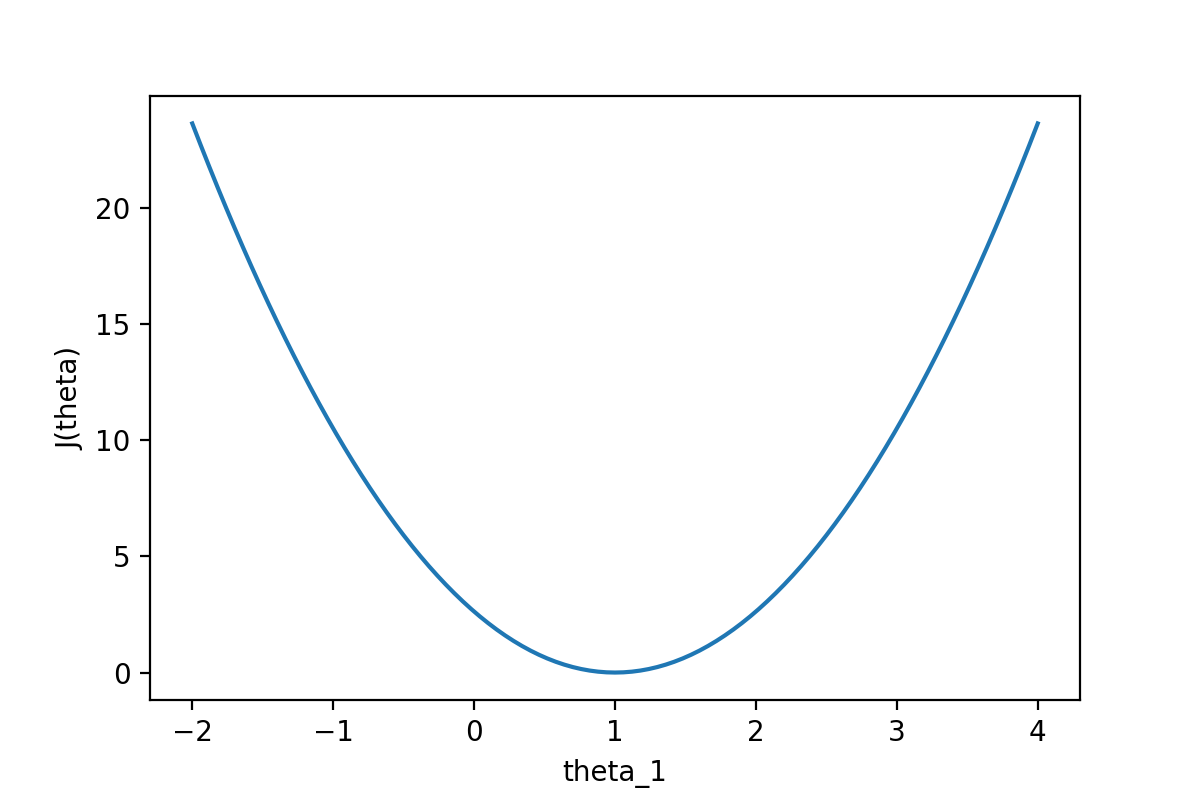
从图中可以很直观的看到θ对代价函数的影响，当θ1=1时，代价函数J(θ)取到最小值。

因为线性回归模型的代价函数（均方误差）的性质非常好，因此也可以直接使用代数的方法，求J(θ)的一阶导数为0的点，就可以直接求出最优的θ值（正规方程法）。

代价函数与梯度

梯度下降中的梯度指的是代价函数对各个参数的偏导数，偏导数的方向决定了在学习过程中参数下降的方向。

学习率（通常用α表示）决定了每步变化的步长，有了导数和学习率就可以使用梯度下降算法（Gradient Descent Algorithm）更新参数了。

下图中展示了只有两个参数的模型运用梯度下降算法的过程。

下图可以看做是代价函数J(θ)与参数θ做出的图，曲面上的一个点 (θ₀, θ₁, J(θ)) ，有无数条切线。

在这些切线中与 x-y 平面（底面，相当于θ₀, θ₁）夹角最大的那条切线就是该点梯度的方向，沿该方向移动，会产生最大的高度变化(相对于z轴，这里的z轴相当于代价函数J(θ))。

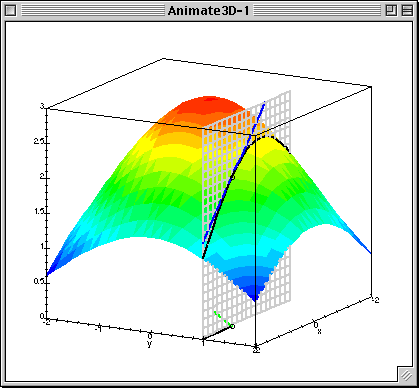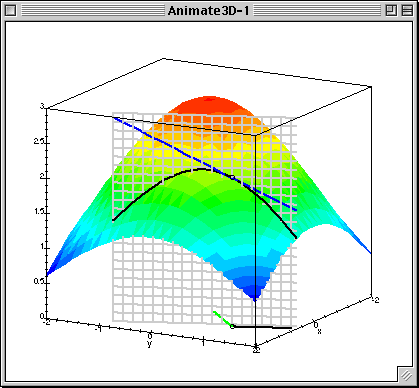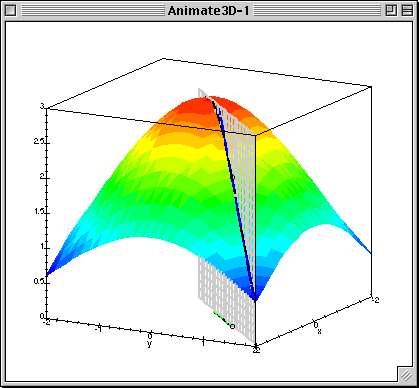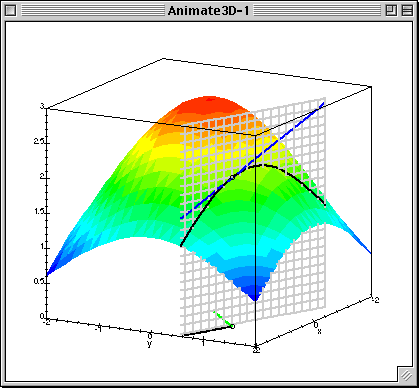
1035701-20170401200538492-1020488011.gif

线性回归模型的代价函数对参数的偏导数

Cost Function

# Cost Function

# 什么是代价函数

# 代价函数的常见形式

# 均方误差

# 交叉熵

# 神经网络中的代价函数

# 代价函数与参数

# 代价函数与梯度

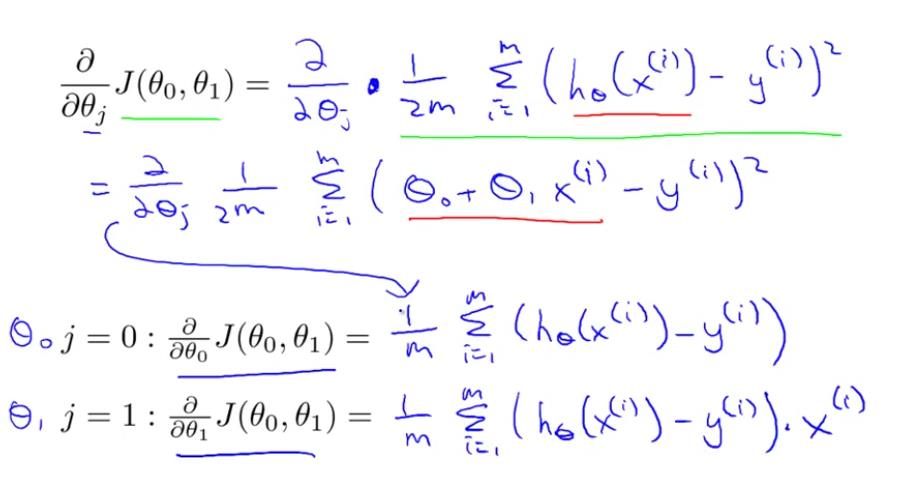
# Reference

Cost Function

什么是代价函数

代价函数的常见形式

均方误差

交叉熵

神经网络中的代价函数

代价函数与参数

代价函数与梯度

Reference