Regularization

正则化是用来防止过拟合的方法。在最开始学习机器学习的课程时，只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数。

成本函数的值不等同于预测误差。我们的目标是使测试数据的预测误差很小。

Underfit and Overfit

• Underfitting: 模型不能很好地拟合数据
• Overfitting：模型与有限的数据集拟合得过于紧密，失去了概括能力

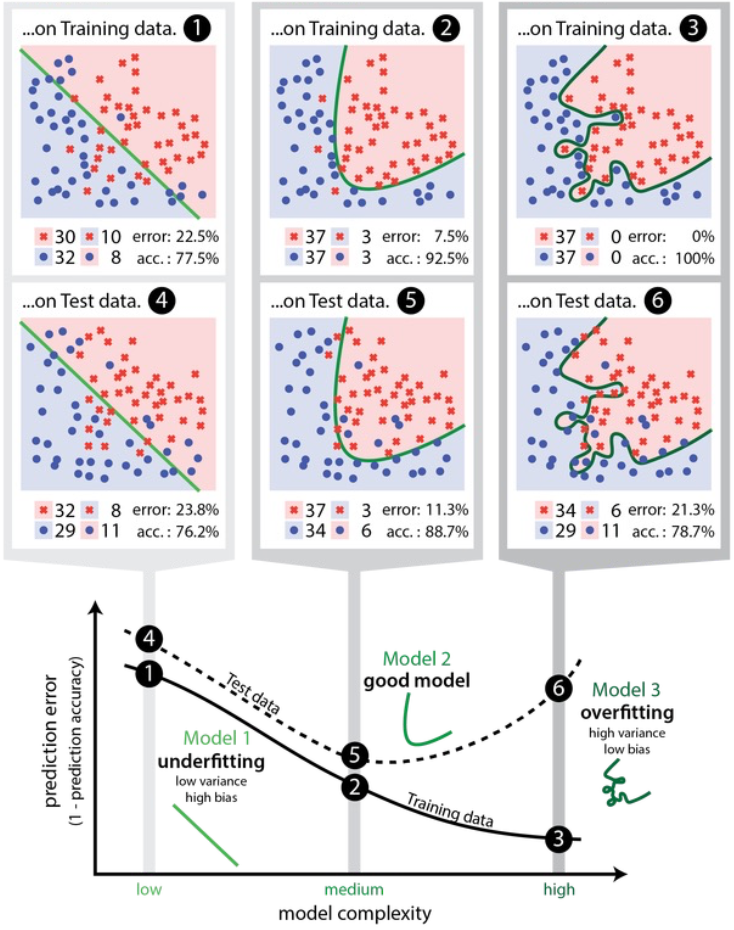
Overfitting

• 如果我们有太多的特征，假设可能非常符合训练集，但不能概括到新的例子（高方差）。
• 更广泛地说，方差也代表了一个模型的结果有多大的相似性，如果它被送入来自同一过程的不同数据。
• 偏差误差来自学习算法中的错误假设。
• 方差误差来自对训练集的小波动的敏感性。

修正 Overfitting 的方法有

• Feature Reduction:
• 手动选择要保留的特征（通过领域知识）
  • 好的，当一些功能真的无用时
• Regularization
  • 保留所有特征，但通过为参数 𝜃i 赋予较小的值来减少它们的影响
  • 好的，当有很多特征时，每个特征都有助于预测𝑦

1676962188199.png

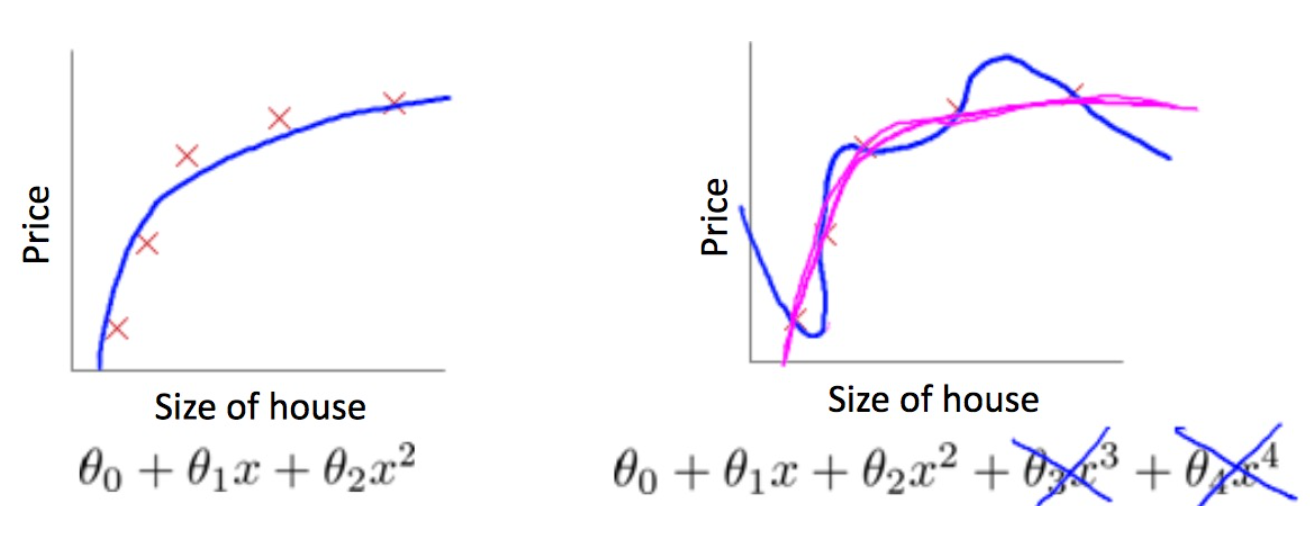
正则化

前面使用多项式回归，如果多项式最高次项比较大，模型就容易出现过拟合。正则化是一种常见的防止过拟合的方法，一般原理是在代价函数后面加上一个对参数的约束项，这个约束项被叫做正则化项（regularizer）。

在线性回归模型中，通常有两种不同的正则化项：

• 加上所有参数（不包括θ₀）的绝对值之和，即 l1 范数，此时叫做 Lasso 回归；
• 加上所有参数（不包括θ₀）的平方和，即 l2 范数的平方，此时叫做 Ridge Regression「岭 回归」。

代价函数的图像

为了可视化，选择直线方程进行优化。假设一个直线方程是 $\hat{h}_{\theta}=\theta_{0}+\theta_{1} x$。该方程只有一个特征x，两个参数 θ₀ 和 θ₁。

该方程的的代价函数为均方误差函数（MSE），为 $J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right)^{2}$ ，其中m 表示样本量。为了保持简单，只取一个样本点 (1,1) 代入上面的代价函数方程中，可得 $J(\theta)=\left(\theta_{0}+\theta_{1}-1\right)^{2}$。图像如下图所示：

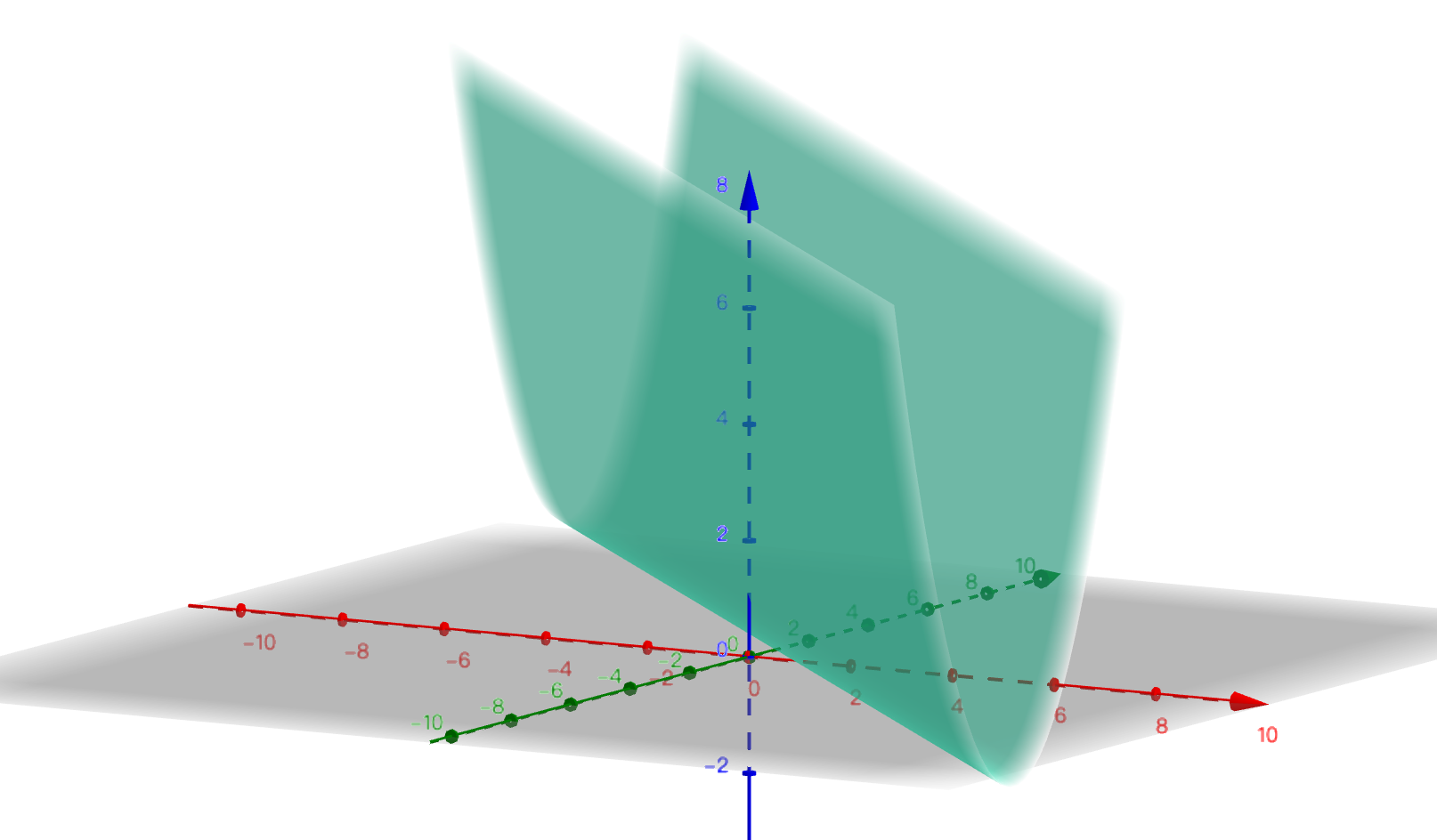
θ₀ 是 红轴，θ₁ 是绿轴。

由于多个样本点的代价函数是所有样本点代价函数之和，且不同的样本点只是相当于改变了代价函数中两个变量的参数（此时θ₀ 和 θ₁是变量，样本点的取值是参数）。因此多样本的代价函数MSE的图像只会在图上发生缩放和平移，而不会发生过大的形变。

目标是将 $J(\theta)$ 的值降到最低。

提示

The regularization term does not include the component of 𝜃₀.

带有正则化项的函数的图像

这里使用L1范数作为正则化项，加上正则化项之后MSE代价函数变成：

$$J(\theta)=\left(\theta_{0}+\theta_{1}-1\right)^{2}J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right)^{2}+\lambda\left\|\theta_{1}\right\|_{1}$$

上式中λ是正则化项的参数，为了简化取λ=1。由于正则化项中始终不包含截距项θ0，此时的L1范数相当于参数θ₁的绝对值。带入1个样本点(1,1) 后，即 $J(\theta)=\left(\theta_{0}+\theta_{1}-1\right)^{2}+\left|\theta_{1}\right|$ ,可以得到下面的图像：

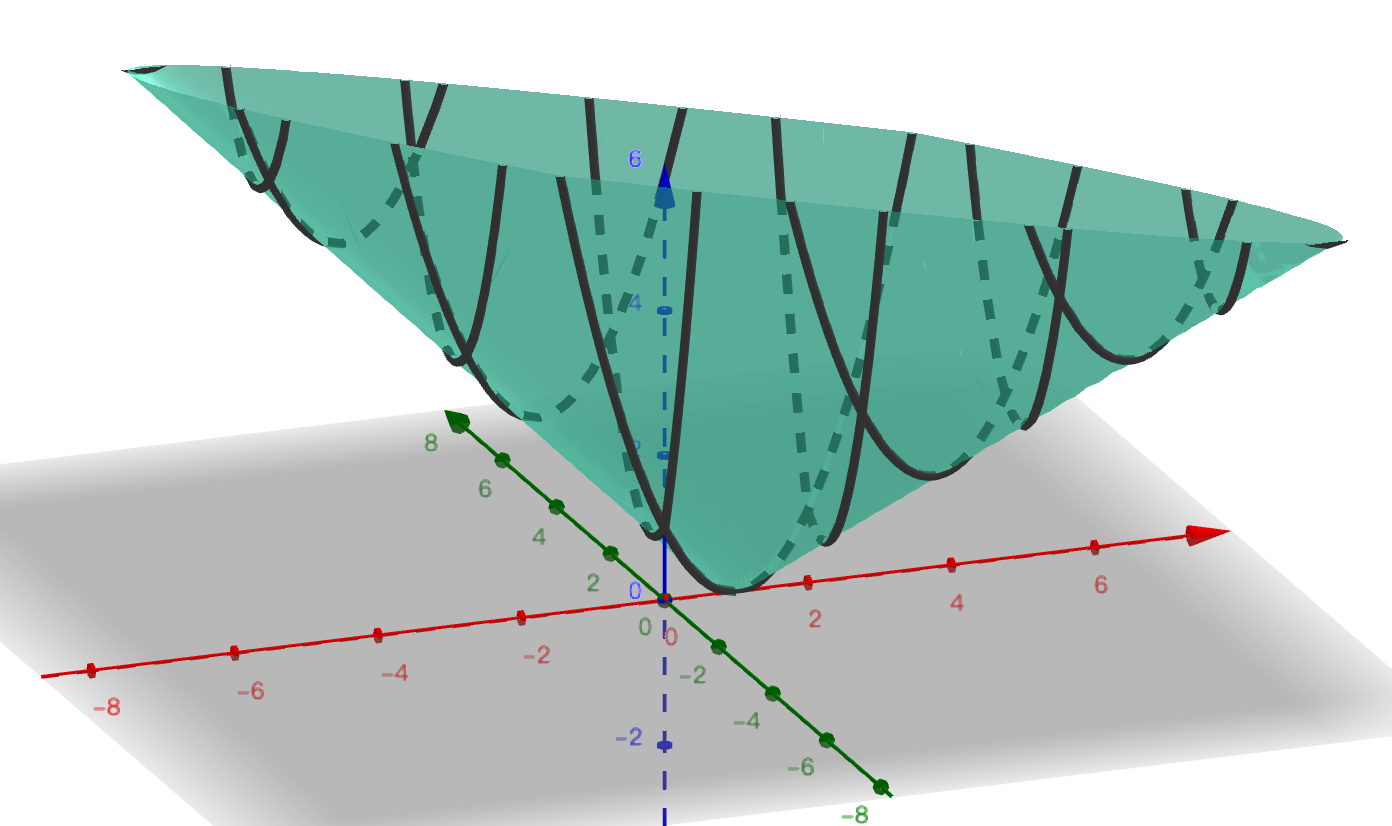
此时的图像，就像是一个圆锥体被捏扁了之后，立在坐标原点上。观察添加正则化项前后的图像，我们会发现：

• 加上正则化项之后，此时损失函数就分成了两部分：第1项为原来的MSE函数，第2项为正则化项，最终的结果是这两部分的线性组合;
• 在第1项的值非常小但在第2项的值非常大的区域，这些值会受到正则化项的巨大影响，从而使得这些区域的值变的与正则化项近似：例如原来的损失函数沿 θ₀ = - θ₁, J轴方向上的值始终为 0，但是加入正则化项J=|θ1|后，该直线上原来为0的点，都变成了θ1的绝对值。这就像加权平均值一样，哪一项的权重越大，对最终结果产生的影响也越大;
• 如果想象一种非常极端的情况：在参数的整个定义域上，第2项的取值都远远大于第一项的取值，那么最终的损失函数几乎100%都会由第2项决定，也就是整个代价函数的图像会非常类似于J=|θ1| 而不是原来的MSE函数的图像。这时候就相当于λ的取值过大的情况，最终的全局最优解将会是坐标原点，这就是为什么在这种情况下最终得到的解全都为0.

岭回归

岭回归 与 多项式回归 唯一的不同在于代价函数上的差别。岭回归的代价函数如下：

$$J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)}-\left(w x^{(i)}+b\right)\right)^{2}+\lambda\|w\|_{2}^{2}=M S E(\theta)+\lambda \sum_{i=1}^{n} \theta_{i}^{2} \quad \cdots(1-1)$$

为了方便计算导数，通常也写成下面的形式：

$$J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y^{(i)}-\left(w x^{(i)}+b\right)\right)^{2}+\frac{\lambda}{2}\|w\|_{2}^{2}=\frac{1}{2} M S E(\theta)+\frac{\lambda}{2} \sum_{i=1}^{n} \theta_{i}^{2} \quad \cdots(1-2)$$

• 上式中的w是长度为 n 的向量，不包括截距项的系数θ₀
• θ 是长度为 n+1 的向量, 包括截距项的系数θ₀
• m 为样本数；n 为特征数

岭回归的代价函数仍然是一个凸函数，因此可以利用梯度等于 0 的方式求得全局最优解（正规方程）：

$$\theta=\left(X^{T} X+\lambda I\right)^{-1}\left(X^{T} y\right)$$

除了上述正规方程之外，还可以使用梯度下降的方式求解（为了计算方便，添加 θ₀=0 到 w）

$$\nabla_{\theta} J(\theta)=\frac{1}{m} X^{T} \cdot(X \cdot \theta-y)+\lambda w$$

在梯度下降的过程中，参数的更新可以表示成下面的公式：

$$\theta=\theta-\left(\frac{\alpha}{m} X^{T} \cdot(X \cdot \theta-y)+\lambda w\right)$$

其中 α 为学习率，λ 为正则化项的参数。

注意

在 sklearn 的 Ridge 模型中，α 参数指的是惩罚系数。

Lasso回归

Lasso回归于岭回归非常相似，它们的差别在于使用了不同的正则化项。最终都实现了约束参数从而防止过拟合的效果。但是Lasso之所以重要，还有另一个原因是：Lasso能够将一些作用比较小的特征的参数训练为0，从而获得稀疏解。也就是说用这种方法，在训练模型的过程中实现了降维(特征筛选)的目的。

Lasso回归的代价函数为：

$$J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y^{(i)}-\left(w x^{(i)}+b\right)\right)^{2}+\lambda\|w\|_{1}=\frac{1}{2} M S E(\theta)+\lambda \sum_{i=1}^{n}\left|\theta_{i}\right|$$

• 上式中的 w 是长度为 n 的向量，不包括截距项的系数 θ₀
• θ 是长度为 n+1 的向量, 包括截距项的系数θ₀
• m 为样本数；n 为特征数
• ||w||_l 表示参数 w 的 l1 范数，也是一种表示距离的函数。加入 w 表示 3 维空间中的一个点 (x,y,z) ，那么 $\|w\|_{1}=|x|+|y|+|z|$ 即各个方向上的绝对值（长度）之和。

上述代价函数的梯度是

$$\nabla_{\theta} M S E(\theta)+\lambda\left(\begin{array}{c} \operatorname{sign}\left(\theta_{1}\right) \\ \operatorname{sign}\left(\theta_{2}\right) \\ \vdots \\ \operatorname{sign}\left(\theta_{n}\right) \end{array}\right)$$

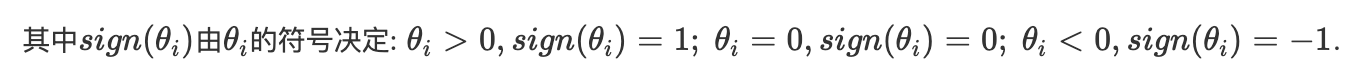
范数

距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。

范数是一种强化的距离概念，它在定义上比距离多了一条数乘的运算法则。有时为了便于理解，我们可以把范数当作距离来理解。

在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样；

对于 $x=\left[x_{1}, x_{2}, \cdots, x_{n}\right]^{\mathrm{T}}$

• L0范数：表示向量x中非零元素的个数。
• L1范数：$|| x||_{1}=\left|x_{1}\right|+\left|x_{2}\right|+\left|x_{3}\right|+\cdots+\left|x_{n}\right|$
• L2范数：$\|x\|_{2}=\left(\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\left|x_{3}\right|^{2}+\cdots+\left|x_{n}\right|^{2}\right)^{1 / 2}$
• Lp范数：$\|x\|_{p}=\left(\left|x_{1}\right|^{p}+\left|x_{2}\right|^{p}+\cdots+\left|x_{n}\right|^{p}\right)^{\frac{1}{p}}$

正则化项的使用

根据吴恩达老师的机器学习公开课，建议使用下面的步骤来确定λ 的值：

1. 创建一个 λ 值的列表，例如 λ ∈ 0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24
2. 创建不同 degree 的 模型（或改变其他变量）;
3. 遍历不同的模型 和 不同的 λ 值;
4. 使用学习到的参数 θ（包含正则化项）计算验证集上的误差（计算误差时不包含正则化项），J_CV(θ)
5. 选择在验证集上误差最小的参数组合（degree和 λ）
6. 使用选出来的参数和λ在测试集上测试，计算J_test(θ)

正则化梯度下降

For Linear Regression with Ridge:

$$h_{\theta}(x)=\theta_{0} x_{0}+\theta_{1} x_{1}+\cdots+\theta_{n} x_{n}$$

$$J\left(\theta_{0}, \theta_{1}, \ldots\right)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$$

$$\frac{\partial J(\theta)}{\partial \theta_{j}}=\frac{1}{m}\left(\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}+\lambda \theta_{j}\right)$$

Repeat until convergence:

$$\theta_{j}=\theta_{j}\left(1-\lambda \frac{\alpha}{m}\right)-\frac{\alpha}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$$

l1与l2的比较

下面通过一张图像来比较一下 岭回归 和 Lasso 回归：

1658407286409.png

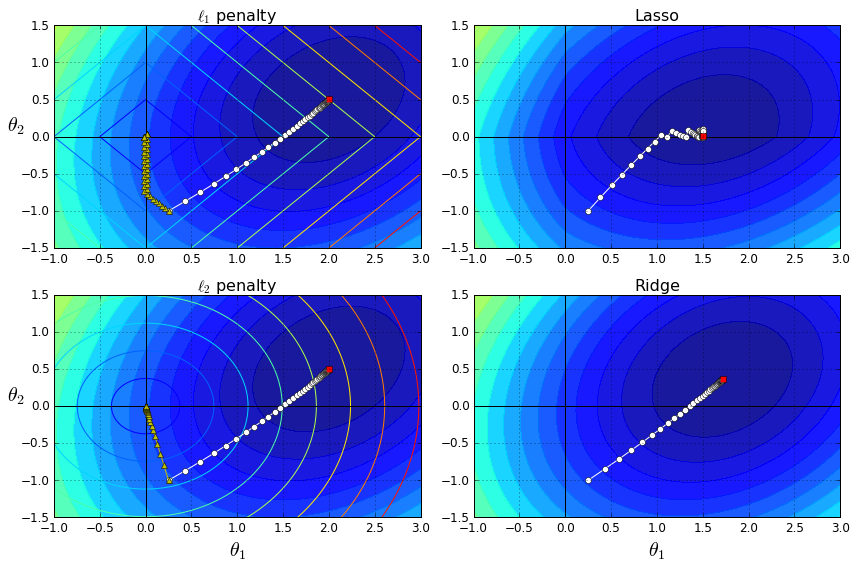
上图中，左上方表示l1（图中菱形图案）和代价函数（图中深色椭圆环）；左下方表示l2（椭圆形线圈）和代价函数（图中深色椭圆环）。同一条线上（或同一个环上），表示对应的函数值相同；图案中心分别表示l1,l2 以及代价函数的最小值位置。

右边表示代价函数加上对应的正则化项之后的图像。添加正则化项之后，会影响原来的代价函数的最小值的位置，以及梯度下降时的路线（如果参数调整合适的话，最小值应该在距离原来代价函数最小值附近且与正则化项的图像相交，因为此时这两项在相互约束的情况下都取到最小值，它们的和也最小）。右上图，显示了Lasso回归中参数的变化情况，最终停留在了θ2=0 这条线上；右下方的取值由于受到了l2 范数的约束，也产生了位移。

当正则化项的权重非常大的时候，会产生左侧黄色点标识的路线，最终所有参数都为0，但是趋近原点的方式不同。这是因为对于范数来说，原点是它们的最小值点。

Reference

• http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html
• Géron A. Hands-on machine learning with Scikit-Learn and TensorFlow: concepts, tools, and techniques to build intelligent systems[M]. " O'Reilly Media, Inc.", 2017. github
• https://www.coursera.org/learn/machine-learning
• edx: UCSanDiegoX - DSE220x Machine Learning Fundamentals