跳至主要內容

Logistic Regression Model

Hirsun, Belter大约 19 分钟

Logistic Regression Model

机器学习很像是一个模型对外界的刺激（训练样本）做出反应，趋利避害（评价标准）。

Classification

  • Binary Classification
  • Multi-class Classification

逻辑回归可以用来解决二分类问题。可以拓展到多分类问题。

提示

  • 回归模型的输出连续的，分类模型的输出是连续的。
  • 严谨的说，逻辑回归不算是回归模型。

什么是逻辑回归

逻辑回归 = 线性回归 + sigmoid函数

从大的类别上来说，逻辑回归是一种有监督的统计学习方法，主要用于对样本进行分类。

在线性回归模型中，输出一般是连续的，例如 y=f(x)=ax+by=f(x)=a x+b ，对于每一个输入的 x，都有一个对应的 y 输出。模型的定义域和值域都可以是 [-∞, +∞] 。

但是对于逻辑回归，输入可以是连续的 [-∞, +∞] ，但输出一般是离散的，即只有有限多个输出值。例如，其值域可以只有两个值 {0, 1} ，这两个值可以表示对样本的某种分类，高/低、患病/健康、阴性/阳性等，这就是最常见的二分类逻辑回归。

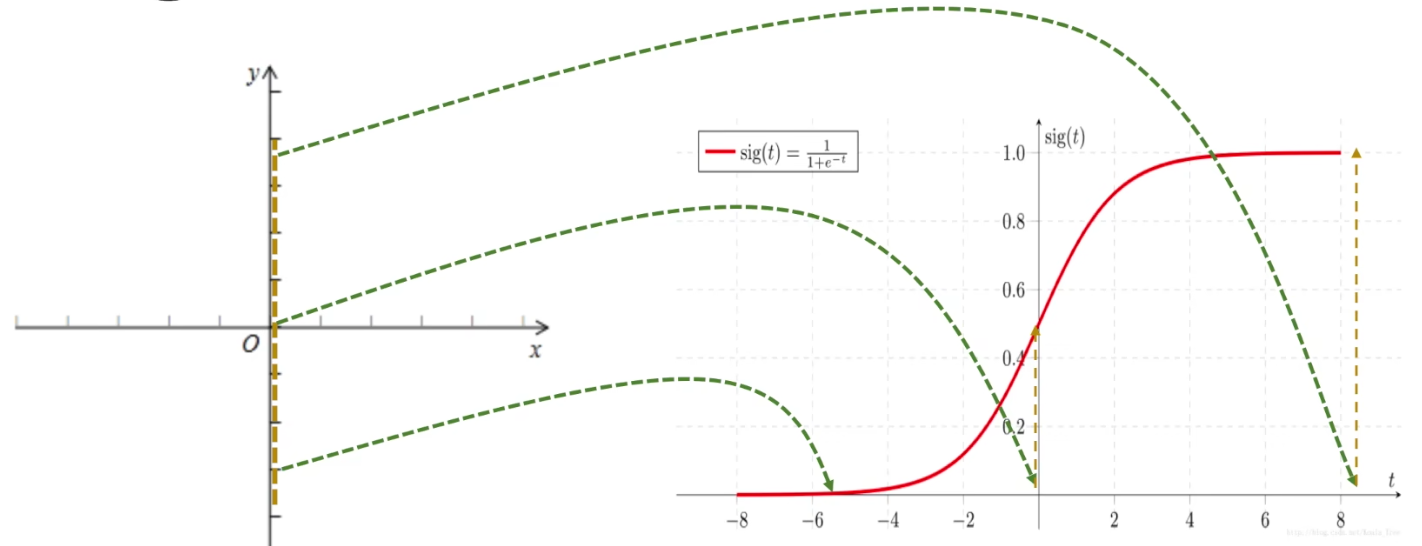
1676958067849.png
1676958067849.png

因此，从整体上来说， 通过逻辑回归模型，我们将在整个实数范围上的x映射到了有限个点上，这样就实现了对x的分类。 因为每次拿过来一个x，经过逻辑回归分析，就可以将它归入某一类y中。

逻辑回归与线性回归的关系

逻辑回归也被称为广义线性回归模型，它与线性回归模型的形式基本上相同，都具有 ax+b ，其中 a 和 b 是待求参数，其区别在于他们的因变量不同

  • 多重线性回归直接将 ax+b 作为因变量，即 y = ax+b
  • logistic 回归 则通过 函数S 将 ax+b 对应到一个隐状态 p，p = S(ax+b)，然后根据 p 与 1-p 的大小决定因变量的值。这里的函数S就是Sigmoid函数。

S(t)=11+e−t S(t)=\frac{1}{1+e^{-t}}

将 t 换成 ax+b，可以得到逻辑回归模型的参数形式：

p(x;a,b)=11+e−(ax+b) p(x ; a, b)=\frac{1}{1+e^{-(a x+b)}}

通用形式是 hθ(x)=11+e−θTxh_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} x}}

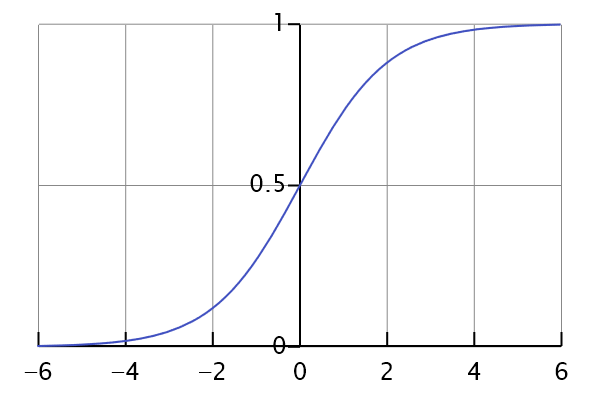
sigmoid函数的图像

S(x)=11+e−xS(x)=\frac{1}{1+e^{-x}}

1657467796254.png

通过 函数S 的作用，我们可以将输出的值限制在区间 (0，1) 上。p(x )则可以用来表示概率 p(y=1|x)，即当一个 x 发生时，y 被分到1那一组的概率。

其实在真实情况下，我们最终得到的y的值是在 [0, 1] 这个区间上的一个数，然后我们可以选择一个阈值，通常是 0.5，当 y>0.5 时，就将这个 x 归到1这一类，如果 y<0.5 就将 x 归到0这一类。

但是阈值是可以调整的，比如说一个比较保守的人，可能将阈值设为0.9，也就是说有超过90%的把握，才相信这个 x 属于1这一类。

对比逻辑回归与线性回归

  • Linear Regression: −∞<hθ(x)<+∞,hθ(x)=θ0x0+θ1x1+⋯+θnxn=θTx-\infty<h_{\theta}(x)<+\infty, \quad h_{\theta}(x)=\theta_{0} x_{0}+\theta_{1} x_{1}+\cdots+\theta_{n} x_{n}=\theta^{T} x
  • Logistic Regression: 0≤hθ(x)≤1,hθ(x)=g(θTx)=11+e−θTx0 \leq h_{\theta}(x) \leq 1, \quad h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}}

Representation

  • hθ(x)h_{\theta}(x) represents the estimated probability that 𝑦 = 1 on input 𝑥
  • hθ(x)h_{\theta}(x) = 𝑃{𝑦=1|𝑥,𝜃} means probability of 𝑦 = 1, given 𝑥, under parameter values 𝜃
  • P{y=0∣x,θ}=1−hθ(x)P\{y=0 \mid x, \theta\}=1-h_{\theta}(x)
CleanShot 2023-02-01 at 16.35.03@2x.png

Decision boundary

θTx=0\theta^{T} x=0 is the decision boundary

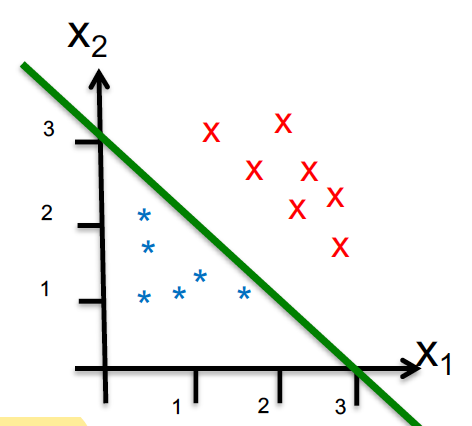
Example:

  • Assume: hθ(x)=g(−3+x1+x2)h_{\theta}(x)=g\left(-3+x_{1}+x_{2}\right)
  • Decision boundary: −3+x1+x2=0-3+x_{1}+x_{2}=0
  • Predict y = 1 when −3+x1+x2⩾0-3+x_{1}+x_{2} \geqslant 0
    • x1+x2⩾3x_{1}+x_{2} \geqslant 3 (red)
1657469988121.png

Regression Metrics

  • MSE: Mean Square Error: 1n∑i=1n(y^t−yt)2\frac{1}{n} \sum_{i=1}^{n}\left(\hat{y}_{t}-y_{t}\right)^{2}
  • MAE: Mean Absolute Error: 1n∑i=1n∣y^t−yt∣\frac{1}{n} \sum_{i=1}^{n}\left|\hat{y}_{t}-y_{t}\right|
  • MAPE: Mean Absolute Percentage Error: 100%n∑i=1n∣y^t−ytyt∣\frac{100 \%}{n} \sum_{i=1}^{n}\left|\frac{\hat{y}_{t}-y_{t}}{y_{t}}\right|

Cost Function

逻辑回归一般使用交叉熵作为代价函数。根据逻辑回归模型的代价函数以及 sigmoid函数

g(z)=11+e−z,hθ(x)=g(θTx) g(z)=\frac{1}{1+e^{-z}}, \quad h_{\theta}(x)=g\left(\theta^{T} x\right)

  • 对一个样本的cost，有 Cost⁡(hθ(x),y)={−log⁡(hθ(x))y=1−log⁡(1−hθ(x))y=0\operatorname{Cost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{cc} -\log \left(h_{\theta}(x)\right) & y=1 \\ -\log \left(1-h_{\theta}(x)\right) & y=0 \end{array}\right.
  • 整体的 Cost Function 为 J(θ)=1m∑i=1mCost⁡(hθ(x(i)),y(i))J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)

这样做是为了 Heavy Penalty， 即

1675262460266.png

注：只观察 [0,1] 区间

Cost Function:

Cost⁡(hθ(x),y)=−ylog⁡hθ(x)−(1−y)log⁡(1−hθ(x)) \operatorname{Cost}\left(h_{\theta}(x), y\right)=-y \log h_{\theta}(x)-(1-y) \log \left(1-h_{\theta}(x)\right)

化简之后为

J(θ)=−1m[∑i=1m(y(i)log⁡hθ(x(i))+(1−y(i))log⁡(1−hθ(x(i)))] J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m}\left(y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]\right.

  • 训练样本的个数；
  • hθ(x)：用参数θ和x预测出来的y值；
  • y：原训练样本中的y值，也就是标准答案
  • 上角标(i)：第i个样本

x(i)x^{(i)}偏导数为

∂J(θ0,θ1,⋯ )∂θj=1m∑i=1m(hθ(x(i))−y(i))xj(i) \frac{\partial J\left(\theta_{0}, \theta_{1}, \cdots\right)}{\partial \theta_{j}}=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}

和线性回归一样，

θj=θj−α∂J(θ0,θ1,⋯ )∂θj \theta_{j}=\theta_{j}-\alpha \frac{\partial J\left(\theta_{0}, \theta_{1}, \cdots\right)}{\partial \theta_{j}}

带有正则化的代价函数

J(θ)=−1m∑i=1m[y(i)log⁡(hθ(x(i)))+(1−y(i))log⁡(1−hθ(x(i)))]+λ2m∑j=1nθj2 J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}

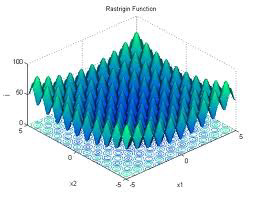
为何逻辑回归要重新定义代价函数

如果在逻辑回归中使用 cost function: J(θ)=1m∑i=1m12(hθ(x(i))−y(i))2J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \frac{1}{2}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} ，其图像为

1657472131550.png
1657472131550.png

这是一个非凸函数，有多个局部最优解，运用梯度下降算法并不会收敛到它的全局最优解。因此我们需要重新定义代价函数。

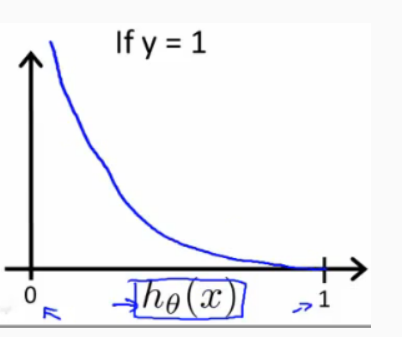
当 y = 1 时，Cost(hθ(x), y) 函数的图像是

1657474758955.png

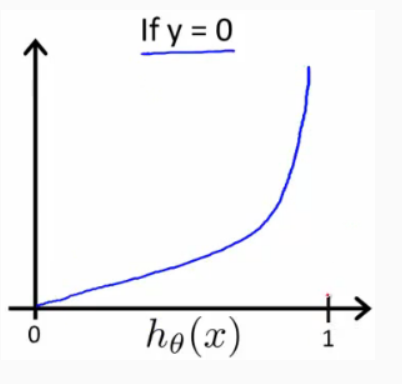
当 y = 0时，Cost(hθ(x), y) 函数的图像是

1657474805716.png
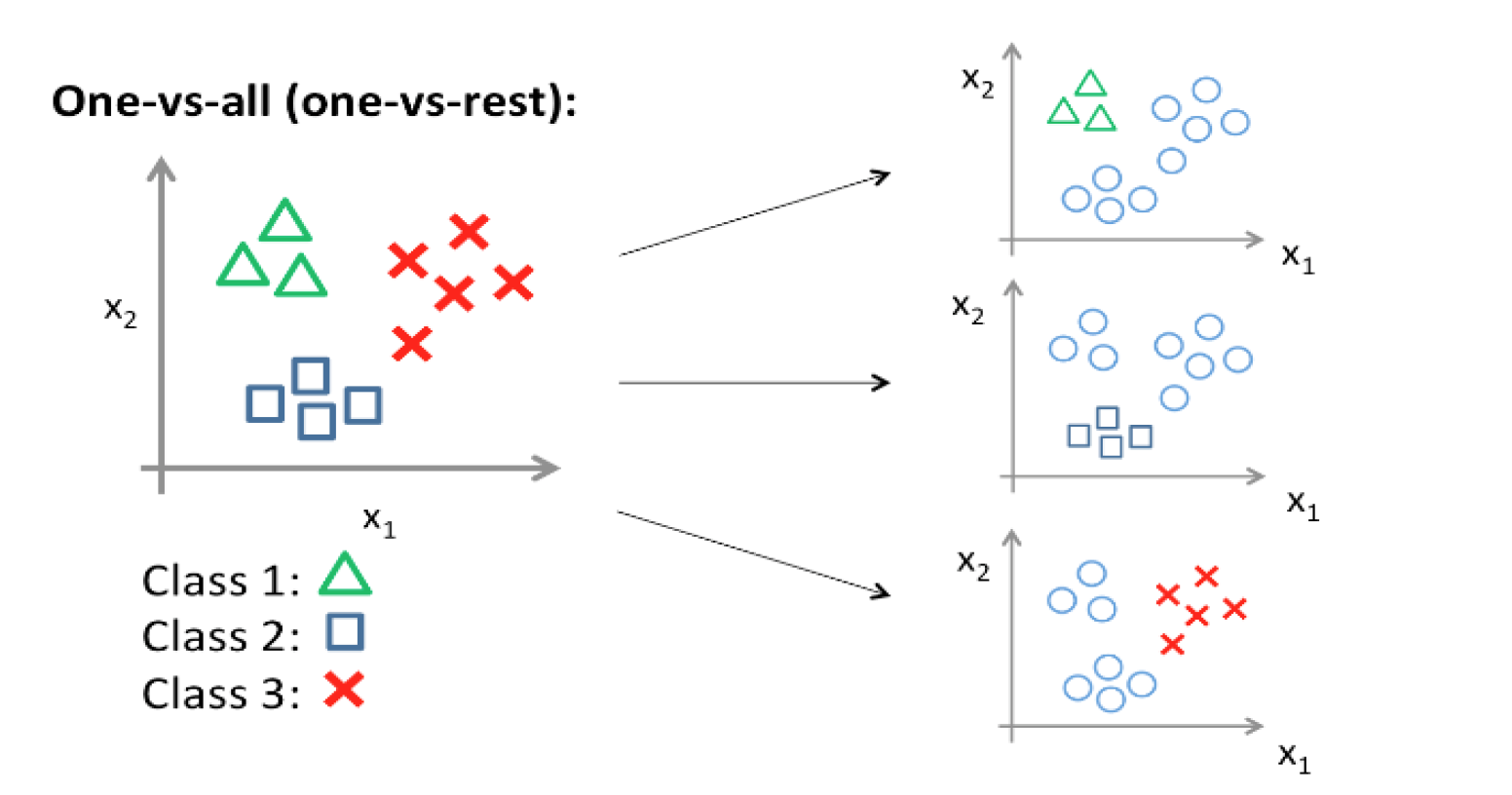
  • 预测正确，那么它的代价值就为 0
  • 预测错误，那么这个代价就是无穷大的

Multi-class Classification

1675263154245.png
1675263154245.png

在 One-vs-all (one-vs-rest) 方法中，为每个类别训练一个二元分类器，将该类别与所有其他类别区分开来。

例如，假设有三个类，A、B、C。在这种情况下，我们将训练三个二元分类器：一个用于A类与其他类的对比，一个用于B类与其他类的对比，一个用于C类与其他类的对比。

1676950789065.png
import numpy as np
from sklearn.linear_model import LogisticRegression

# create a toy dataset with three classes
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7]])
y = np.array([0, 1, 2, 1, 0, 2])

# create three binary classifiers, one for each class
classifiers = []
for i in range(3):
    y_binary = (y == i).astype(int)
    clf = LogisticRegression()
    clf.fit(X, y_binary)
    classifiers.append(clf)

# predict the class of a new instance
new_instance = np.array([[2.5, 3.5]])
scores = [clf.predict_proba(new_instance)[0][1] for clf in classifiers]
predicted_class = np.argmax(scores)

# Note that the argmax function returns the index of the highest score, which corresponds to the original class label in this example.
print("Predicted class:", predicted_class)
Legends never die | Serving since 2011.
Copyright © 2024 Hirsun, Belter