Association Rule Mining

Hirsun大约 44 分钟

Association Rule Mining

什么是关联规则挖掘（ARM）？-> find frequent patterns

关联规则挖掘（Association Rule Mining）是一种在大型数据库中寻找有趣关联或模式、频繁项集、关联规则等的方法。这个概念最初是在购物篮分析中提出的，用于发现顾客购买行为中的模式。例如，如果一个顾客购买了面包，他/她可能也会购买牛奶。这样的规则可以用于商品放置、促销活动、个性化推荐等。

关联规则挖掘的主要步骤包括：

频繁项集挖掘：找出频繁出现在数据集中的项集。例如，在一组购物数据中，面包和牛奶可能经常一起出现。
规则生成：基于频繁项集生成有趣的关联规则。例如，购买面包的顾客可能也会购买牛奶。

这个过程涉及到两个主要的度量参数：支持度和置信度。支持度是一个项集在所有交易中出现的频率，而置信度是一个规则在给定前提的条件下成立的频率。

一个经典的算法用于关联规则挖掘是Apriori算法。这个算法利用了一个项集的子集也是频繁的这个属性来减少需要检查的项集数量，从而提高了效率。

Frequent Pattern Analysis

频繁模式：数据集中频繁出现的模式（子序列、子结构等）
动机：发现数据的内在规律
- 啤酒和尿布经常一起购买吗？
- 购买个人电脑后还会购买哪些产品？
- 哪些 DNA 对这种新药敏感？
- 我们能自动对网络文档进行分类吗？
应用领域：购物篮数据分析、交叉营销、目录设计、促销活动分析、网络日志（点击流）分析和 DNA 序列分析

为什么频繁模式「Frequent Pattern」很重要？

披露数据集的内在和重要属性
为许多基本数据挖掘任务奠定基础
- 关联、相关和因果分析
- 顺序、结构（例如子图）模式
- 时空、多媒体、时间序列和流数据中的模式分析
- 分类：关联分类
- 聚类分析：基于频繁模式的聚类
- 数据仓库：冰山立方体和立方体梯度
- 广泛的应用

基本概念

给定：

交易数据库
每笔交易都是一份物品清单

查找：将一组物品的存在与另一组物品的存在联系起来的所有规则。比如，98% 的人在购买轮胎和汽车配件的同时也会获得汽车服务

应用领域：

* -> 维护协议（商店应如何促进维护协议的销售）
家用电子产品 -> * （商店还应该储备哪些产品？）

Support and Confidence are rule measures.

目的是以最小的置信度和支持度找到 X => Z 的所有规则

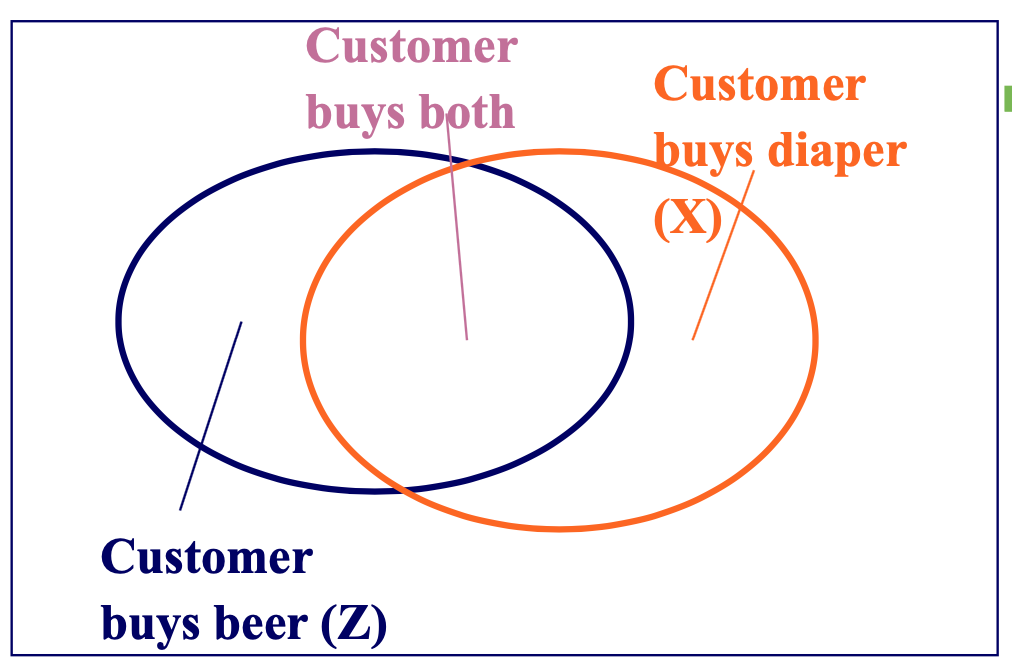
support， s，交易同时包含 X 和 Z 的概率
confidence，c，具有 X 的交易也包含 Z 的条件概率

Support

Given the association rule X -> Z , the support is the percentage of records consisting of X & Z together, i.e. Supp.= P(X & Z )
indicates the statistical significance (统计显著性) of the association rule.

Confidence

Given the association rule X -> Z, the confidence is the percentage of records also having Z, within the group of records having X, i.e. Conf.= P(Z| X )
数据集中 itemset {X} 和itemset {Z} 之间的相关度。
is a measure of the rule's strength

Variants of ARM

布尔关联与定量关联（基于处理的数值类型）
- buys(x, “SQLServer”) ^ buys(x, “DMBook”) -> buys(x, “DBMiner”) [0.2%, 60%]
- age(x, “30..39”) ^ income(x, “42..48K”) -> buys(x, “PC”) [1%, 75%]
单维与多维关联（参见上面的示例）
单级与多级分析
- 什么品牌的啤酒与什么品牌的尿布有关？
各种扩展
- 相关性、因果关系分析
- 交易间关联规则挖掘
- 顺序关联规则挖掘
- 强制执行的约束
  - E.g., small sales (sum < 100) trigger big buys (sum > 1,000)?

AR Mining Algorithm - Apriori

“任何频繁项集的子集都必须是频繁的”这句话是关联规则挖掘中的一个基本原理，这是基于“Apriori原理”。

算法步骤

Apriori算法主要用于在数据库中找到频繁项集，即那些在数据库中经常一起出现的项的集合。这个算法主要包括两个步骤：连接步骤和剪枝步骤。

1. 假设Lk-1中的项按顺序排列（例如，{B D A E}被排序为{A B D E}）
   
// Mining Frequent Itemsets
2. Step 1: self-joining Lk-1 插入到 Ck
   a. 选择 p.item1, p.item2, ..., p.itemk-1, q.itemk-1
   b. 来自 Lk-1 p, Lk-1 q
   c. 其中 p.item1=q.item1, ..., p.itemk-2=q.itemk-2, p.itemk-1 < q.itemk-1
   
// Rule Generation from Frequent Itemsets
   
3. Step 2: pruning
   a. 对Ck中的所有项集c执行以下操作：
      i. 对c的所有(k-1)-子集s执行以下操作：
         1. 如果s不在Lk-1中，则从Ck中删除c

Mining Frequent Itemsets

Mining Association Rules: A Key Step − Mining Frequent Itemsets

在关联规则挖掘（Association Rule Mining，ARM）中，挖掘频繁项集（Mining Frequent Itemsets）确实是一个关键步骤，这是因为频繁项集是生成关联规则的基础。

Two key steps in AR mining:

Frequent Itemset Mining: Find the frequent itemsets, i.e. the sets of items that have minimum support - Apply the Apriori principle:A subset of a frequent itemset must also be a frequent itemset
Rule Generation: Iteratively find the frequent itemsets with cardinality from 1 to k(-itemset)

子集与超集

如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集，集合B称为集合A的超集。

我们要从只包含一个元素的项集开始，逐步增加项集中的元素个数，直到k个元素，来迭代地找到所有的频繁项集。例如，假设我们有以下事务数据集：

1: A, B, C
2: B, C, D
3: A, C, D
4: A, B, D
5: B, C, D

我们设定最小支持度为60%。

我们首先找1-项集（只包含一个物品的项集）的频繁项集。

{A} 的支持度是 3/5 = 60%
{B} 的支持度是 4/5 = 80%
{C} 的支持度是 4/5 = 80%
{D} 的支持度是 4/5 = 80%

所有的1-项集都是频繁的。接下来，我们找2-项集（包含两个物品的项集）的频繁项集。我们只考虑之前找到的频繁1-项集的组合：

{A, B} 的支持度是 2/5 = 40%
{A, C} 的支持度是 2/5 = 40%
{A, D} 的支持度是 2/5 = 40%
{B, C} 的支持度是 3/5 = 60%
{B, D} 的支持度是 3/5 = 60%
{C, D} 的支持度是 3/5 = 60%

所以，频繁的2-项集有：{B, C}、{B, D}和{C, D}。最后，我们找3-项集（包含三个物品的项集）的频繁项集。我们只考虑之前找到的频繁2-项集的组合：

{B, C, D} 的支持度是 2/5 = 40%

所以，没有频繁的3-项集。

另外一个案例是

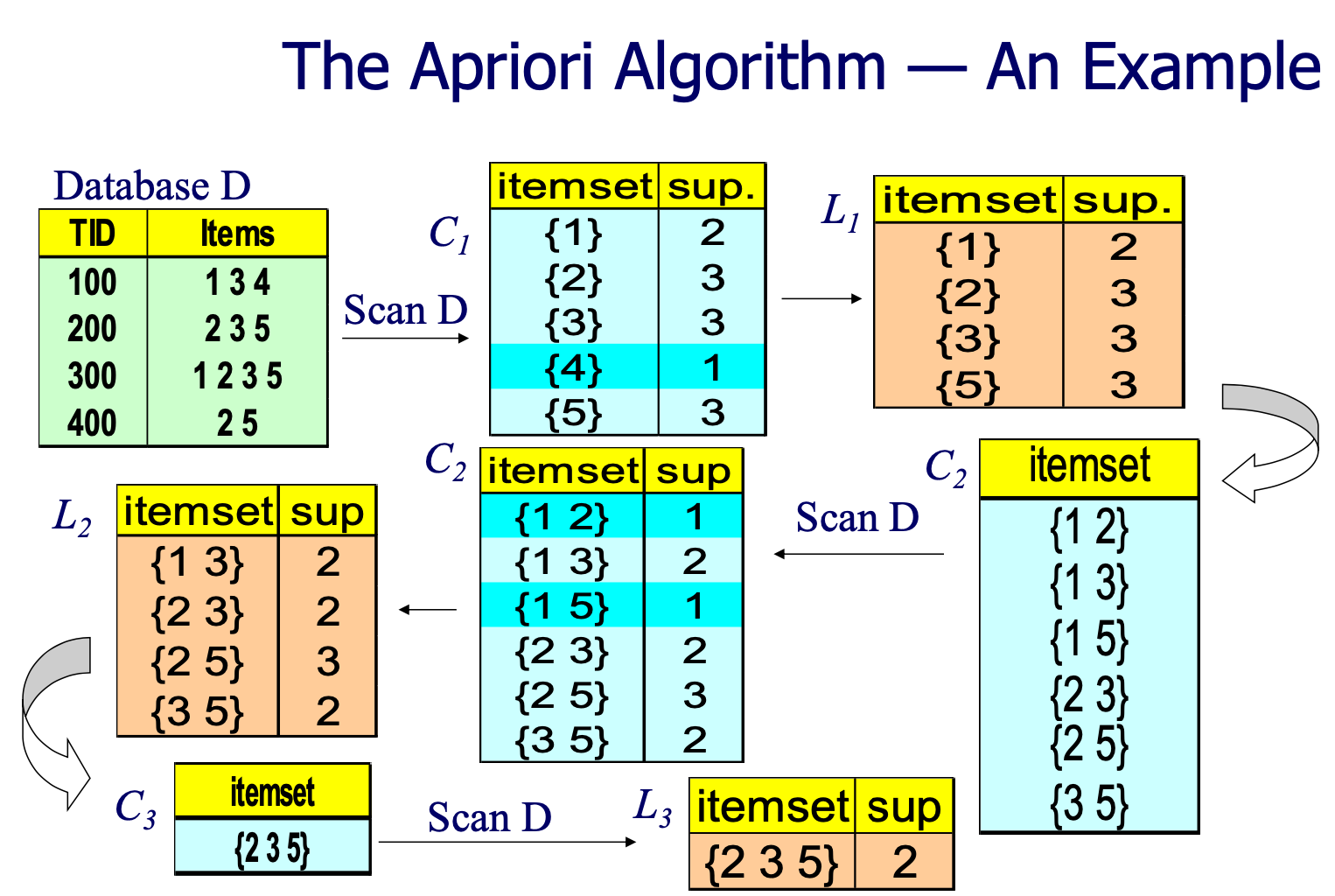
Generate Candidates

“Generate Candidates”指的是在关联规则挖掘过程中，生成候选项集的过程。在Apriori算法中，这是一个重要的步骤，其目的是为了找到频繁项集，从而能够生成关联规则。

提示

在关联规则中，

Lk-1 表示包含 k-1 个项的频繁项集的集合
Ck 代表候 选 k 项 集的集合。
在每一轮迭代中，我们根据 Lk-1 中的频繁项集生成 Ck

Ck中的项集可能是频繁的，也可能是非频繁的，因为在这个阶段我们还没有计算它们的支持度。Ck中的项集需要进一步的测试和验证来确定哪些是真正的频繁项集。

自连接（Self-Joining）: 将 Lk-1 与自身进行连接，生成 Ck。
- 比如，如果 L3-1（即 L2）包含 {A, B} 和 {A, C}，那么通过自连接可以得到 C3 项集 {A, B, C}。
- 但是，注意连接的条件，p.itemk-1 < q.itemk-1 确保了每个项集都是唯一的，不会产生重复。
剪枝（Pruning）: 删除 Ck 中任何非频繁子集的项集。如果一个候选 k 项集的任何 k-1 子集不在 Lk-1 中，那么该项集就被从 Ck 中删除，因为它不可能是频繁的。

p.itemk-1 和 q.itemk-1 分别代表集合 p 和集合 q 的最后一个项

生成 C_k 的常用方法是自连接 L_k-1，并对结果进行剪枝，确保 C_k 中每个项集的所有子集都是频繁的。

为什么要生成候选项集

生成候选项集是为了在大数据集上，找到满足最小支持度阈值的频繁项集。

在实际的数据中，可能有成千上万的项和成千上万的事务，如果直接计算每个可能的项集的支持度，将会非常低效，甚至不可行。
通过生成候选项集，我们可以减小搜索空间，避免不必要的计算。

Apriori 算法中的生成候选项集

在Apriori算法中，生成候选项集的步骤通常包括两个主要的部分：自连接和剪枝

L2 = {{A,B}, {A,C}, {B,D}, {C,D}}

Step1 自连接: 对 L2 进行自连接以生成 C3 = {{A,B,C},{A,B,D},{A,C,D},{B,C,D}}
Step2: 剪枝: 接下来我们要进行剪枝，从 C3 中删除所有包含非频繁子集的项集。例如，{A, B, C} 的子集 {B, C} 不在 L2 中，所以 {A, B, C} 不是频繁的，会被从 C3 中删除。
最后，剩下的项集构成了新的候选集 C3。

此过程是 Apriori 算法的一部分，它利用了这样一个事实：所有非频繁（不满足最小支持度要求）的项集的超集也一定是非频繁的。通过自连接和剪枝步骤，我们能够有效地生成下一级的候选频繁项集。

另外一个例子

Rule Generation

The Final Step: Rule Generation from

Apriori 算法使用支持度来挖掘频繁项集，而规则生成步骤使用置信度来限定关联规则的强度。

在找到频繁项集之后，Apriori算法的最后一步是生成关联规则。关联规则的形式是“X -> Y”，其中X和Y是项集，且X ∩ Y = ∅。关联规则的目的是在数据中找到X和Y之间的关系。这些规则是通过频繁项集及其子集生成的，并且它们满足一定的最小置信度阈值。

规则生成步骤包括：

生成非空子集：对于每个频繁项集 L，生成 L 的所有非空子集
规则生成：对于L的每个非空子集 s，生成规则 R：s -> (L-s)。
置信度检验：如果规则 R 满足最小置信度，即： conf (s->(l-s)) = support(L) / support(s) >= min_conf 则规则R是一个强关联规则，并应该被输出。

Example

假设我们有以下频繁项集L和它的支持度：

L = {A, B, C}, support(L) = 0.6

我们要找到所有可能的关联规则，并检查它们是否满足最小置信度（假设min_conf = 0.7）。

生成非空子集：{A}, {B}, {C}, {A, B}, {A, C}, {B, C}
生成规则：
- {A} -> {B, C}
- {B} -> {A, C}
- {C} -> {A, B}
- {A, B} -> {C}
- {A, C} -> {B}
- {B, C} -> {A}
检验规则：例如，对于规则{A} -> {B, C}
- 计算置信度：conf(A->B，C) = support(A,B,C)/support(A)
- 如果conf(A -> B,C) >= 0.7, 则输出规则{A} -> {B, C}。

通过这个过程，我们可以找到所有满足最小支持度和最小置信度的关联规则。

Comments on Apriori

Is Apriori Fast Enough? — Performance Bottlenecks

The core of the Apriori algorithm: Use frequent (k-1)-itemsets to generate candidate frequent kitemsets
Use database scaning and pattern matching to collect counts for the candidate itemsets

The bottleneck of Apriori: candidate generation

Huge candidate sets
- 10^4 frequent 1-itemset will generate > 10^7 candidate 2-itemsets
- To discover a frequent pattern of size 100, e.g., {a1, a2, ..., a100}, one needs to generate 2^100 = 10^30 candidates.
Multiple scans of database: Needs (n +1 ) scans, where n is the length of the longest pattern

Methods to Improve Apriori’s Efficiency

基于散列的项目集计数：对应散列桶计数低于阈值的项目集不能是频繁项目集
事务减少：不包含任何频繁k项集的事务在后续扫描中是无用的
分区：数据库中可能频繁出现的任何项集必须在数据库的至少一个分区中频繁出现
采样：挖掘给定数据的子集，下支持阈值+确定完整性的方法
动态项目计数：只有当所有子集估计为频繁出现时，才添加新的候选项目集

Criticism to Support and Confidence

在关联规则挖掘中，支持度和置信度是两个核心的度量标准。然而，它们也受到一些批评，主要是因为它们可能不总是能够准确地捕捉到项集之间的关系。让我们通过给出的例子来探讨这个问题。

Objective measures「客观衡量」 - Two popular measurements: support and confidence
Subjective measures 「主管衡量」 - 如果满足以下条件，则规则（模式）很有趣：
- 出乎意料（令用户惊讶）；和/或
- 可操作（用户可以用它做一些事情）

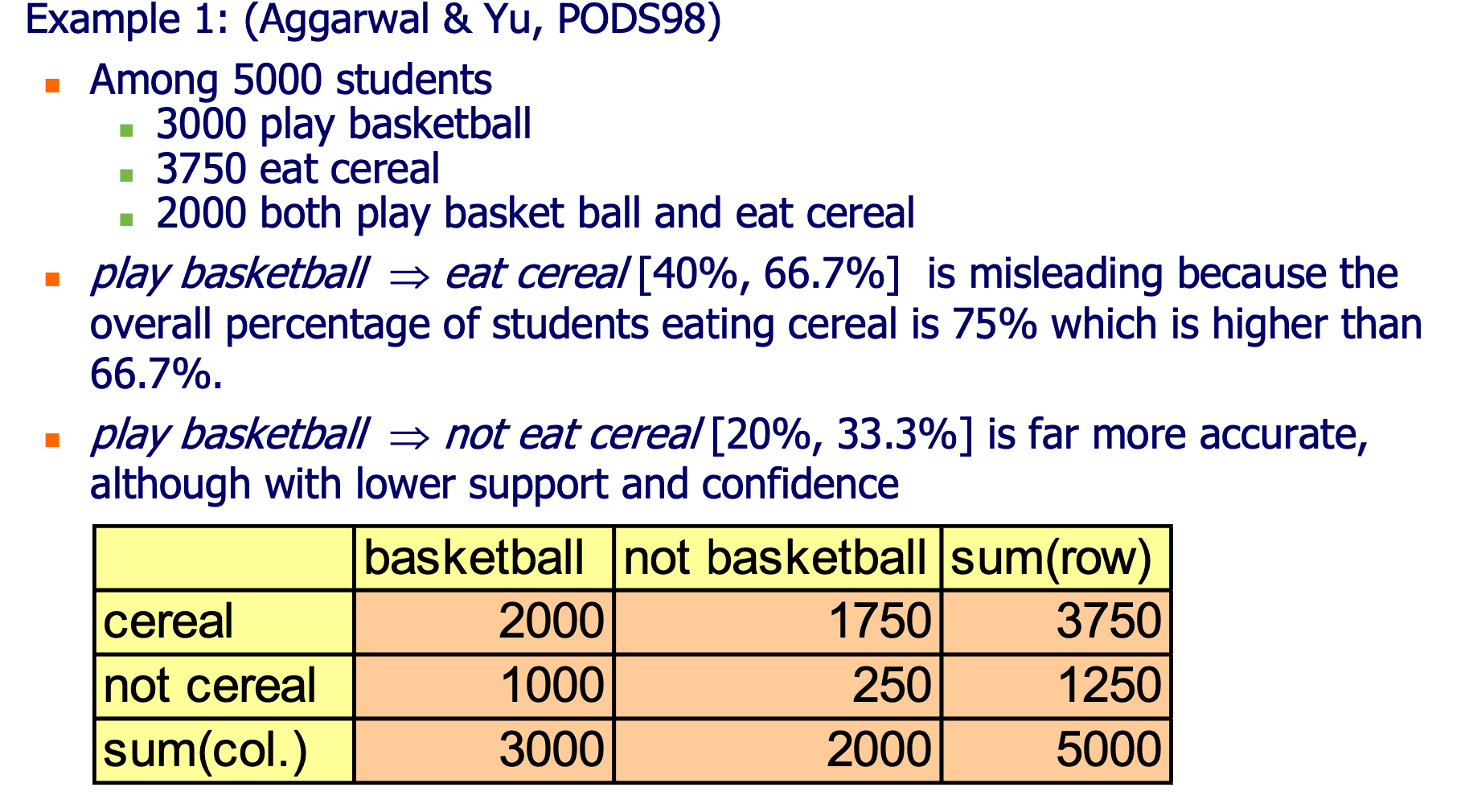
提示

案例1 的本质问题与条件概率的应用有关。

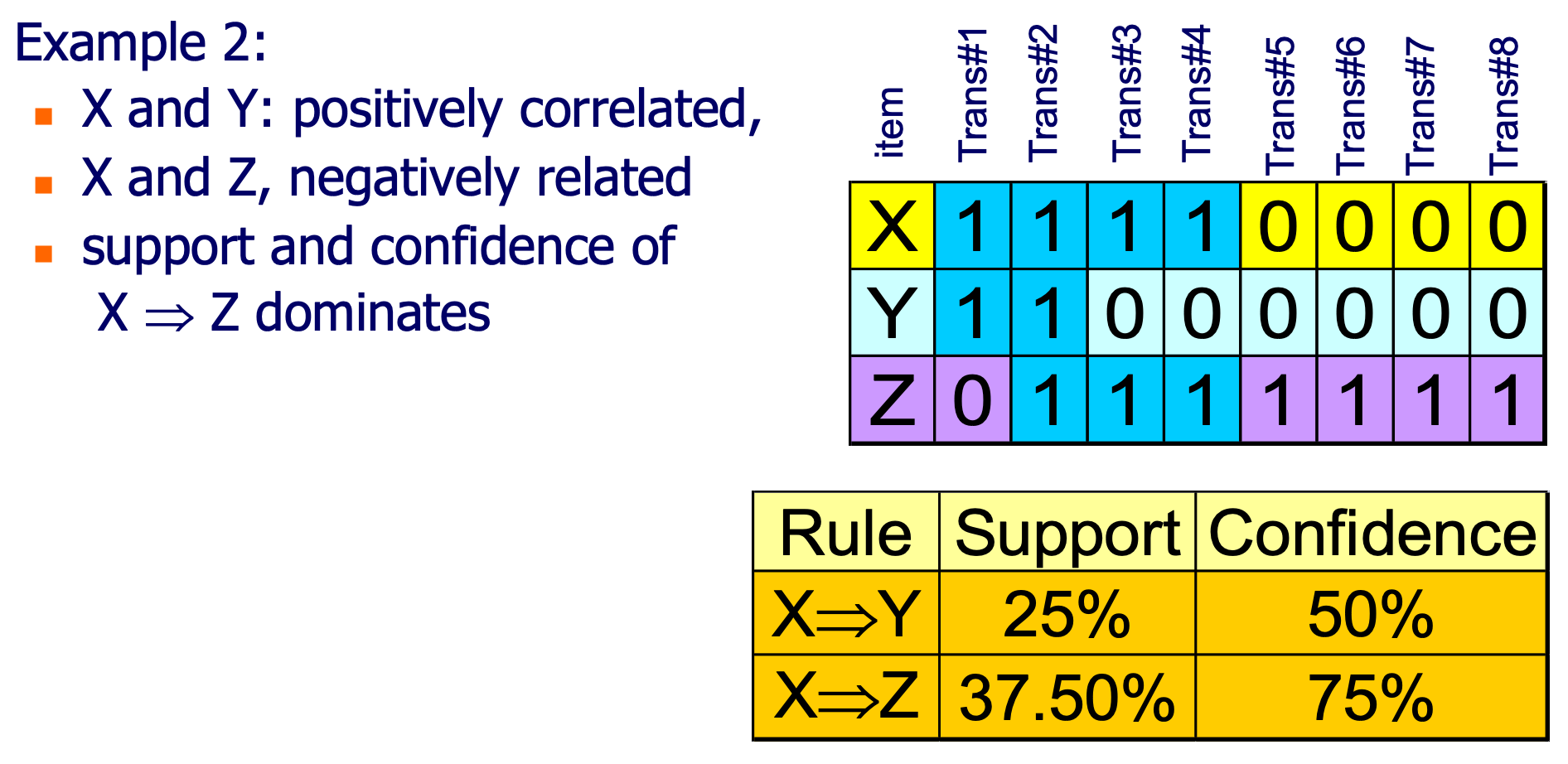
根据这些度量，我们可能会认为规则 X -> Z 比 X -> Y 更强，因为它有更高的支持度和置信度。然而，这可能忽略了一些潜在的关系。

问题点：

忽略了其他变量的影响：置信度和支持度不考虑其他可能影响关系的变量。例如，在这个例子中，尽管 X -> Z 的支持度和置信度较高，但我们不能确定这是否是由于其他变量（例如Y）的影响。
忽略了负关系：支持度和置信度不能捕捉到负关系。在这个例子中，X和Z可能是负相关的，但是如果我们只看支持度和置信度，我们可能会得出错误的结论。
不平衡的数据分布：如果数据分布不平衡，支持度和置信度可能会给出误导。例如，如果Z在大多数事务中都是1，那么任何与Z相关的规则的支持度和置信度都可能会很高，不一定因为它们有实际的关联关系。

Interes

Other Interestingness Measures -> Interes

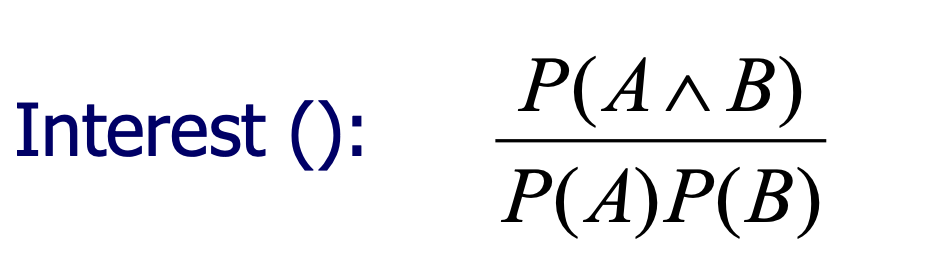
同时考虑 P(A) 和 P(B)
如果 A 和 B 是独立事件，P(A^B)=P(B)*P(A)
如果值小于 1，则 A 和 B 负相关；否则A和B正相关
a kind of correlation analysisc → correlation 「相关性」不是 association
也称为 A->B 的关联规则的 lift(ratio) （将 B 的可能性提升一个返回值的因子）

Association Rule Mining

# Association Rule Mining

# Frequent Pattern Analysis

# 基本概念

# Support

# Confidence

# Variants of ARM

# AR Mining Algorithm - Apriori

# 算法步骤

# Mining Frequent Itemsets

# Generate Candidates

# 为什么要生成候选项集

# Apriori 算法中的生成候选项集

# Rule Generation

# Comments on Apriori

# Criticism to Support and Confidence

# Interes

Association Rule Mining

Frequent Pattern Analysis

基本概念

Support

Confidence

Variants of ARM

AR Mining Algorithm - Apriori

算法步骤

Mining Frequent Itemsets

Generate Candidates

为什么要生成候选项集

Apriori 算法中的生成候选项集

Rule Generation

Comments on Apriori

Criticism to Support and Confidence

Interes