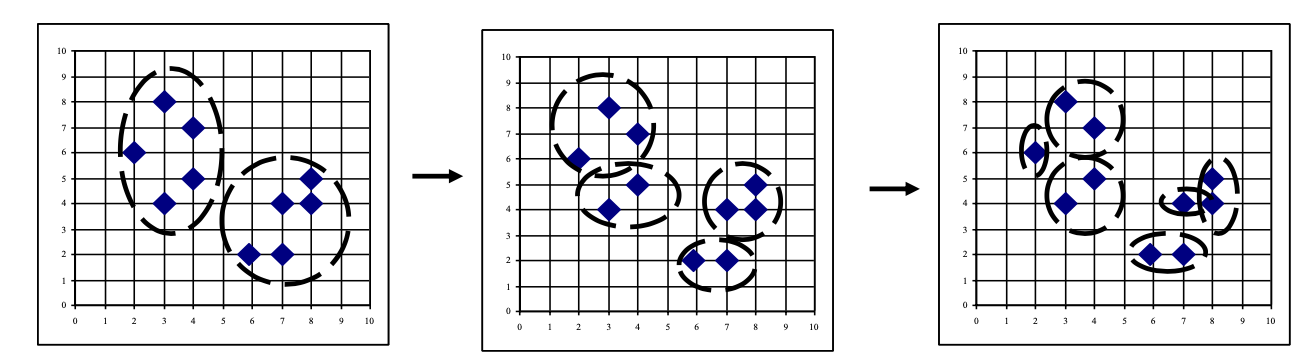
Clustering

Hirsun大约 66 分钟

Clustering

What is a Cluster? Cluster Analysis? Clustering?

Cluster: 数据对象的集合，这些对象是
- 同一集群内的彼此相似
- 与其他簇中的对象不同
Cluster analysis: 将一组数据对象分组为簇
聚类(Clustering) 是一种无监督学习方法，没有预定义的类（或监督信号）
聚类并不排除分类/回归。它有助于分类/回归！

典型应用

作为深入了解数据分布的独立工具
作为其他算法的预处理步骤

General Applications

Spatial「空间」 Data Analysis
- 通过聚类特征空间在 GIS 中创建专题地图
- 检测空间聚类并在空间数据挖掘中解释它们
图像处理（参见通过肤色像素聚类进行人脸检测）
经济科学（尤其是市场研究；客户分组）
WWW
- 文件分类
- 对博客数据进行聚类以发现相似访问模式组

Specific Examples

营销：帮助营销人员发现客户群中的不同群体，然后利用这些知识制定有针对性的营销计划
土地利用：在地球观测数据库中识别类似土地利用的区域
保险：识别平均索赔成本较高的汽车保险保单持有人群体
城市规划：根据房屋类型、价值和地理位置识别房屋组

Good Clustering

良好的聚类方法将产生高质量的聚类
- high intra-class similarity
- low inter-class similarity
聚类结果的质量取决于该方法所使用的相似性度量及其实现。
聚类方法的质量还可以通过其发现部分或全部隐藏模式的能力来衡量。

Requirements of Clustering in Data Mining

Scalability 「可扩展性」
ability to deal with different types of attributes 「处理不同类型属性的能力」
Discovery of clusters with arbitrary shape 「发现任意形状的簇」
Minimal requirements for domain knowledge to determine input parameters 「确定输入参数对领域知识的最低要求」
能够处理噪音「noise」和异常值「outliers」
对输入记录的顺序不敏感
High dimensionality「高纬度」
Incorporation of user-specified constraints 「合并用户指定的约束」
Interpretability and usability「可解释性和可用性」

Measure of Quality

具体衡量方法

Normalized Mutual Information (NMI) [see sklearn.metrics.NMI] 「归一化」
Rand Index [see Wiki] 「兰德指数」

两者都衡量两个数据聚类之间的相似性（例如，真实情况与聚类结果）

Dissimilarity/Similarity metric「度量」：相似性以距离函数 d(i, j) 表示
有一个单独的 “quality” function 来衡量集群的“goodness”。
对于区间尺度变量、布尔变量（二元变量）、分类变量和序数变量，距离函数的定义通常非常不同。
权重应根据应用程序和数据语义与不同的变量相关联。

很难定义“足够相似”或“足够好”，答案通常非常主观。

Data Structures

Data matrix

object-by-variable structure（n 个对象和 p 个变量/属性）

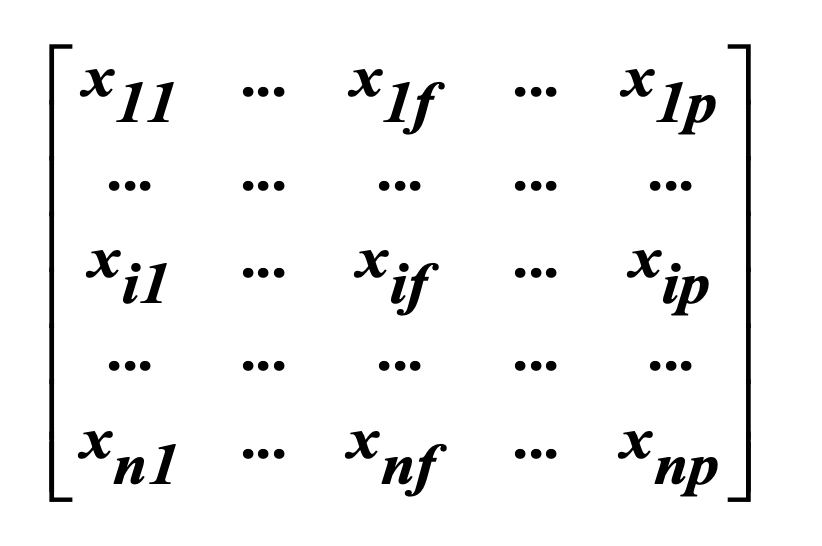
对象（Object）：通常指的是数据集中的个体样本，例如在人口统计学研究中的每个人，或在产品调查中的每个产品。
变量（Variable）/属性（Attribute）：指的是每个对象的特征或属性，例如人的年龄、性别，或产品的价格、颜色。

Dissimilarity matrix

不相似度矩阵”（Dissimilarity Matrix）是一种用于表示数据对象之间差异或不相似性的表格。在这种矩阵中，每一行和每一列都代表数据集中的一个对象，而矩阵中的每个元素表示对应两个对象之间的不相似度。

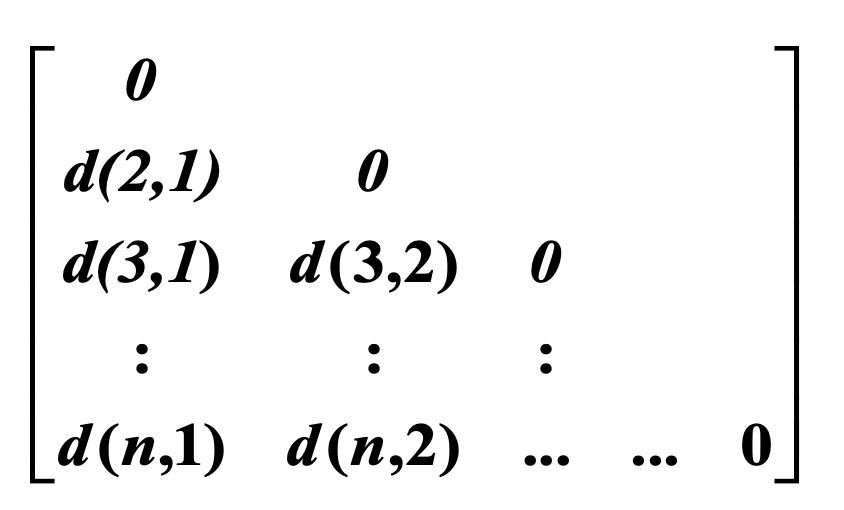
对象（Object）：数据集中的个体，如人、物品、事件等。
不相似度（Dissimilarity）：衡量两个对象之间差异的数值。这个数值越大，表示两个对象越不相似；数值越小，表示两者越相似。

Example

假设我们有一个关于四个城市（A、B、C、D）的数据集，我们想要根据各种因素（如气候、人口、经济）来评估这些城市之间的不相似性。不相似度矩阵可能如下所示：

	A	B	C	D
A	0	2	4	7
B	2	0	3	6
C	4	3	0	5
D	7	6	5	0

行和列：代表城市。
数值：例如，A和B的不相似度为2，意味着它们在某种程度上相似；而A和D的不相似度为7，意味着它们差异很大。

这种矩阵在诸如聚类分析、模式识别等领域非常有用，因为它提供了对象之间差异的量化方法。

混淆定义

距离(不相似度) 和相似度不要算反了，两个相加=1.

Distance Measure

Objects

距离「Distances」通常用于衡量两个数据对象之间的相似性或不相似性

Some popular ones include Minkowski distance (L_q norm):

d(\vec{i},\vec{j})=\left(\left|\vec{x}_{i1}-\vec{x}_{j1}\right|^q + \left|\vec{x}_{i2}-\vec{x}_{j2}\right|^q + \ldots + \left|\vec{x}_{ip}-\vec{x}_{jp}\right|^q\right)^{\frac{1}{q}}

where $\vec{i} = (x_{i1}, x_{i2}, \ldots, x_{ip})$ and $\vec{j} = (x_{j1}, x_{j2}, \ldots, x_{jp})$ are 两个(p)维数据对象，(q)是一个正整数

Minkowski 距离是一种常见的距离计算方式，它可以根据参数q的不同变化为不同的距离度量方法。这个公式本质上是在计算两个点在空间中的距离，这两个点由它们的属性或特征（如坐标）来定义。

If q=1, d is Manhattan (or city block) distance (L₁ norm)

d(\vec{i}, \vec{j})=\left|x_{i_{1}}-x_{j_{1}}\right|+\left|x_{i_{2}}-x_{j 2}\right|+\ldots+\left|x_{i_{p}}-x_{j p}\right|

当q=1时，Minkowski距离就变成了曼哈顿距离，它通过计算两个点在各个维度上差值的绝对值之和来衡量距离。想象你在一个城市的街区中行走，只能沿着街道（东西或南北）走，那么从一个地点到另一个地点的最短路径就是它们的曼哈顿距离。

If q=2, d is Euclidean distance: (L₂ norm)

d(\vec{i}, \vec{j})=\sqrt{\left(\left|x_{i_{1}}-x_{j_{1}}\right|^{2}+\left|x_{i_{2}}-x_{j_{2}}\right|^{2}+\ldots+\left|x_{i_{p}}-x_{j_{p}}\right|^{2}\right)}

Properties

d(i,j) >= 30
d(i,i)=0
d(i,j) = d(j,i)
d(i,j) <= d(i,k)+d(k,j)

此外，还可以使用加权距离、参数皮尔逊积矩相关性或其他相异性度量。

Binary Variables

A contingency table for binary data

用来衡量两个对象在二元变量上的相似性或差异性。在这个表中，对象i和对象j要么具有某个属性（用1表示），要么不具有（用0表示）。

表中的字母a、b、c和d代表以下内容：

a：对象i和对象j都是1的次数。
b：对象i是1而对象j是0的次数。
c：对象i是0而对象j是1的次数。
d：对象i和对象j都是0的次数。
p：总次数，即所有情况的和，也就是a+b+c+d。

在二元数据分析中，有两种常用的相似性/距离衡量方法：

简单匹配系数（Simple Matching Coefficient, SMC）：它考虑了所有的相似和不相似（即所有的a、b、c和d）。

相似度： SMC = (a+d)/(a+b+c+d)
距离/不相似度： d(i,j) = (b+c)/(a+b+c+d)

这个系数是“不变的”，意味着它不区分哪些是正匹配（都有属性）和哪些是负匹配（都没有属性）。

杰卡德系数（Jaccard Coefficient）：这个系数仅考虑了两个对象在同时为1的情况下的相似比例，忽略了同时为0的情况。

相似度： Jaccard = (a)/(a+b+c) = 交集/并集
距离/不相似度： d(i,j) = (b+c)/(a+b+c)

提示

在二元数据分析中，二元属性可以是对称的（symmetric）或非对称的（non-symmetric）。

对称属性意味着属性的两种状态（通常是0和1）在数据分析的语境中具有同等的重要性。也就是说，一个属性是1或是0，两者都同样重要，并且没有一个比另一个在分析中更重要。
- 考虑一个关于电影评价的属性，其中1表示“喜欢”（like），0表示“不喜欢”（dislike）。在这种情况下，无论观众喜欢还是不喜欢一部电影，这两种情况都同样重要，因为我们同样关心有多少人喜欢电影和有多少人不喜欢电影。
非对称属性是指在数据分析中，属性的两种状态中有一种明显比另一种更重要或更值得注意。通常，非对称属性的一个状态（通常是1）代表了某种特殊情况，而另一个状态（通常是0）则是正常或默认情况。
- 考虑一个医疗数据集中的“疾病”属性，其中1表示“有疾病”，0表示“无疾病”。在大多数情况下，我们对发现疾病的情况（1）更感兴趣，因为它需要进一步的诊断和治疗，而无疾病的情况（0）是正常状态。因此，这是一个非对称属性，因为两个状态的分析重要性是不平等的。

在使用不同的相似性或不相似性度量时，识别属性是对称还是非对称的很重要，因为它会影响选择哪种系数来计算相似性或距离。例如，简单匹配系数（SMC）适用于对称属性，而杰卡德系数忽略了共同的非存在（都是0的情况），因此适用于非对称属性。

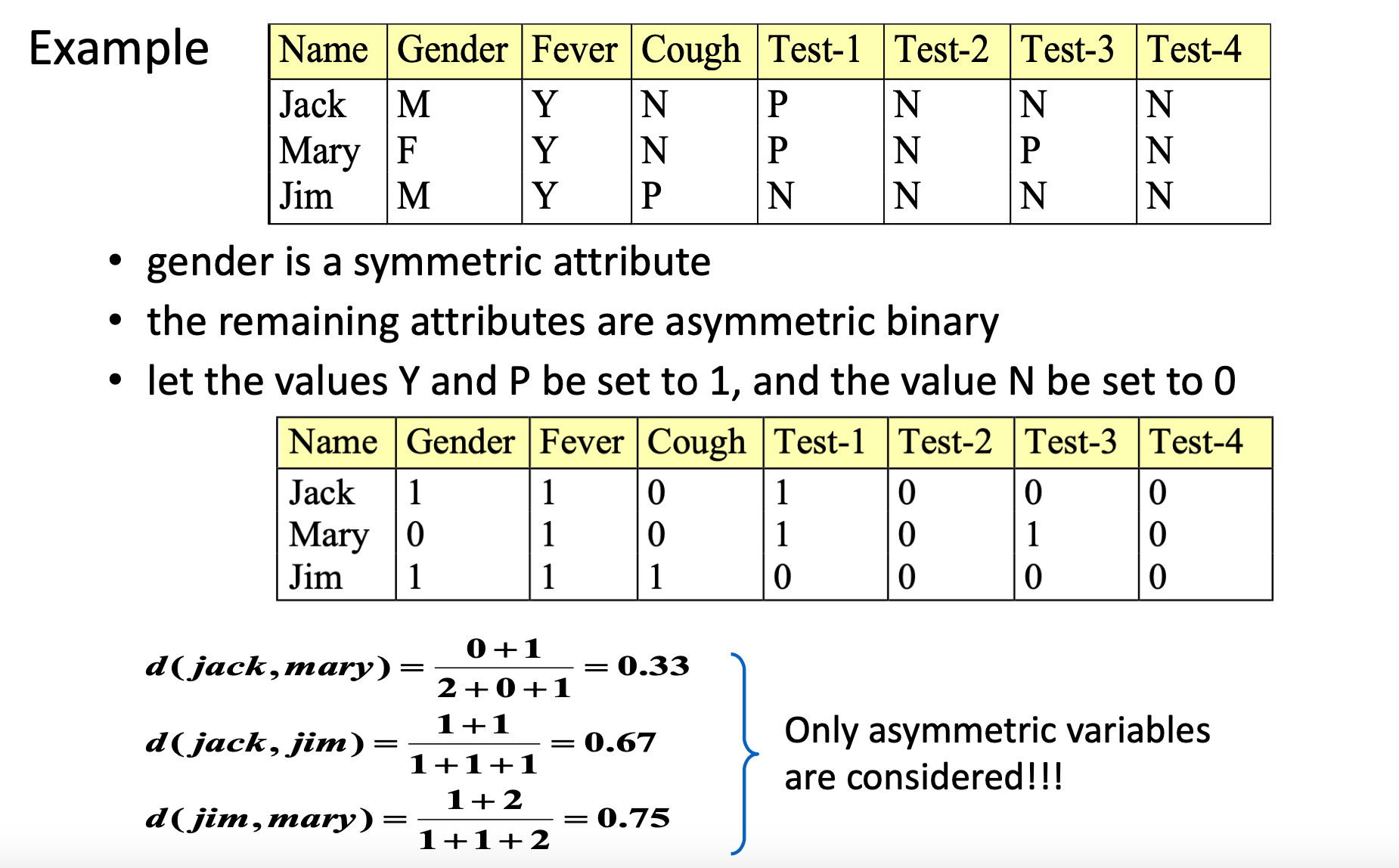
Example

假设我们有两个群体（我们称它们为群体i和群体j）正在对同一部电影的多个情节做出反应，他们可以表达是否喜欢这部电影的一些情节，每个情节反应一次。在这个例子中，我们用1来表示喜欢，0表示不喜欢。

a（同时喜欢）：20次
b（i喜欢，j不喜欢）：5次
c（i不喜欢，j喜欢）：10次
d（同时不喜欢）：15次

用简单匹配系数计算相似度：SMC = (20 + 15) / (20 + 5 + 10 + 15) = 35 / 50 = 0.7

用杰卡德系数计算相似度：Jaccard = 20 / (20 + 5 + 10) = 20 / 35 ≈ 0.57

这意味着根据简单匹配系数，两个群体有70%的相似度；而根据杰卡德系数，考虑到只有喜欢的情况，两个群体的相似度是57%。

另外一个案例是

Nominal/Categorical Variables

二元变量的概括，它可以采用 2 种以上的状态，例如红、黄、蓝、绿

方法一：简单搭配

m：匹配数
p：变量总数

d(i, j) = (p-m)/p

方法2：使用大量二进制变量

1-hot encoding: 为 M 个标称状态中的每一个创建一个新的二进制变量

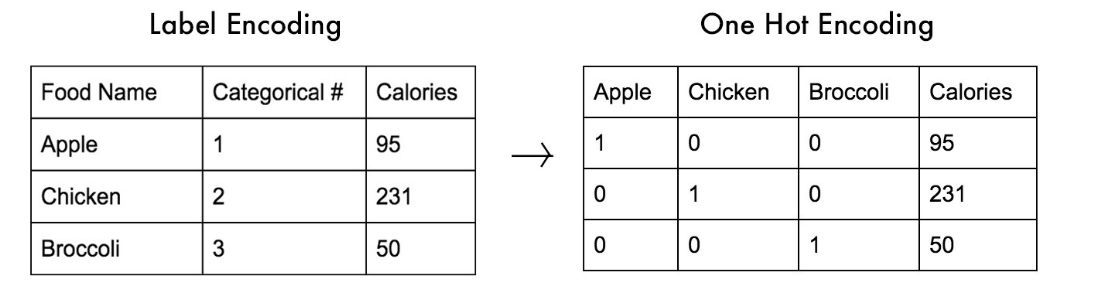
Transactional Data

这里的交易数据是指由一系列项（如商品、服务或事件）组成的数据记录，它们通常出现在购物篮分析、顾客购买历史或其他类型的数据库中，如事件日志。

通常用 Jaccard Similarity

Jaccard\ Similarity = \frac{|A \cap B|}{|A \cup B|}

where ∩ & ∪ denote the intersection and union of two transaction records respectively.

Let T1= {A,B,C}, T2={C,D,E} where A-E denote items

\operatorname{Sim}\left(T_{1}, T_{2}\right)=\frac{|\{C\}|}{|\{A, B, C, D, E\}|}=\frac{1}{5}

Major Clustering Approach

分区算法「Partitioning algorithms」：构造各种分区，然后根据某些标准对其进行评估
分层算法「Hierarchical algorithms」：使用某些标准创建数据集（或对象）的分层分解

这两个在一般应用中最为人熟知

基于密度「Density-based」：基于连通性和密度函数
基于网格「Grid-based」：基于多级粒度结构
基于模型「Model based」：为每个群组假设一个模型，目的是找到该模型与其他群组的最佳匹配度

Partitioning Algorithms

分区方式：将包含 n 个对象的数据库 D 的分区构造为一组 k 个簇。

给定一个特定的 k，找到 k 个簇的分区，以优化所选的分区标准（例如，高类内相似度）

Two methods

全局最优方法：穷举所有分区（对于大n几乎不可能）
启发式方法：k-means 和 k-medoids 算法
- k-means (MacQueen’67)：每个簇由簇的中心表示
- k-medoids 或 PAM（围绕中心点划分）（Kaufman & Rousseeuw’87）：每个簇由簇中的一个对象表示

K-Means Clustering Method

给定 k，k-means 算法可以通过以下四个步骤实现：

初始化（Initialization）：首先，随机选择k个数据点作为初始的簇中心（也称为种子点）。这些点代表了每个簇的起始位置。
初始化的簇的生成是基于选择数据点最近的种子点的最短距离相应的簇。
计算质心（Mean-op）：对于每个簇，计算所有属于该簇的数据点的平均位置，这个平均位置就是簇的新质心。质心是该簇内所有点的平均位置，可以看作是簇的“中心”。
分配到最近的质心（Nearest_Centroid-op）：接下来，重新检查每个数据点，将其分配给最近的质心所代表的簇。这个步骤确保了每个数据点都属于与其最近的簇。
重复迭代：重复步骤2和步骤3，直到达到一个停止条件——通常是质心不再显著变化，或者数据点的簇归属不再改变。

可以在 https://www.naftaliharris.com/blog/visualizing-k-means-clustering/open in new window 查看 Demo

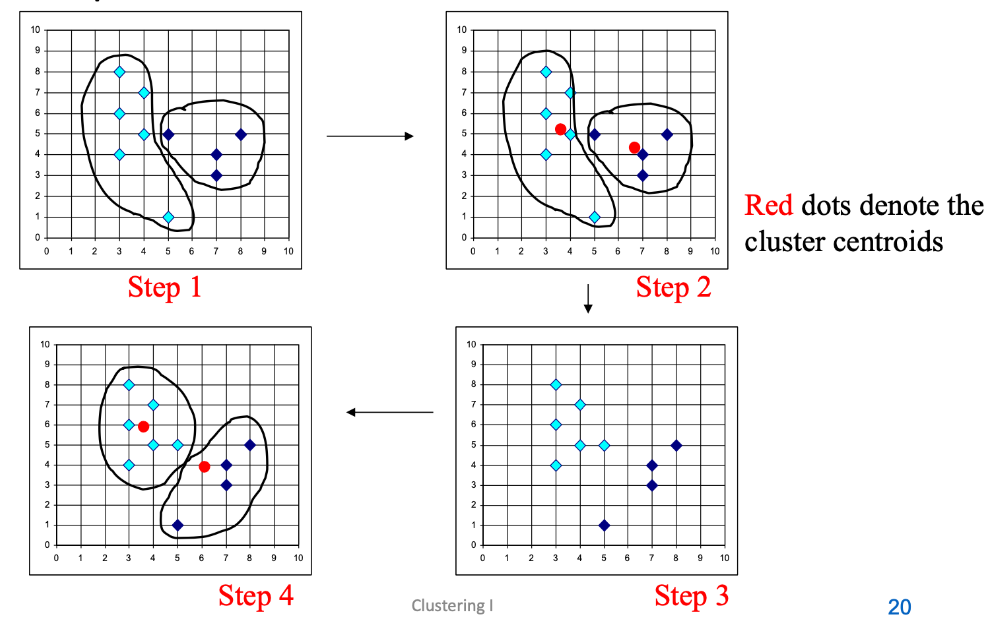
Centroid 是集群中所有（数据）点的平均值。这意味着中心点是一个 "人工 "点。区别于 Clustroid，对比请参考 Centroid & Clustroid

Example

初始化：从客户数据中随机选取3个客户作为初始簇中心。
计算质心：计算每个簇中客户购物数据的平均值，这个平均值表示每个簇的新质心。
分配到最近的质心：根据每个客户的购物数据，将他们分配给最近的质心所代表的簇。
重复迭代：不断重复计算质心和重新分配客户，直到质心的位置稳定下来，这意味着每个客户都被归入了最适合他们购物习惯的簇中。

Comments

Strength

相对高效：O(tkn)，其中 n 是 # 个对象，k 是 # 个簇，t 是 #iterations。通常，K，t << n。
通常终止于局部最优。可以使用确定性退火和遗传算法等技术找到全局最优值

Weakness

仅在定义均值时适用，那么分类数据呢？
红色、橙色、蓝色分别代表什么意思？
需要提前指定k，簇的数量
无法处理嘈杂的数据和异常值
不适合发现非凸形状的簇；簇的基本形状是球形（凸形）

Variations of K-Means Method

k 均值存在几种变体，它们的不同之处在于：

初始 k 均值的选择
相异性计算
计算聚类平均值的策略

K-Medoids Clustering Method

K-Medoids聚类方法与K-Means类似，但 K-Medoids 使用的是 Clustroid: 一个现有的（数据）点，与集群中所有其他点 "最接近"。

在簇中查找代表性对象，称为中心点
K-Medoids对异常值更加鲁棒，因为它选择实际存在的数据点作为中心，而不是所有点的平均。
PAM (Partitioning Around Medoids, 1987) 对于小数据集有效，但对于大数据集扩展性不佳

Choosing k

由应用程序定义，例如图像量化
绘制数据图（降维后）并检查聚类
增量（领导者簇）算法：一次添加一个，直到“肘部”（重建误差/对数似然/组间距离）
手动检查含义

Hierarchical Clustering

聚类过程涉及一系列数据分区: 它可以运行包含所有记录的单个群集，也可以运行包含单个记录的 n 个群集。

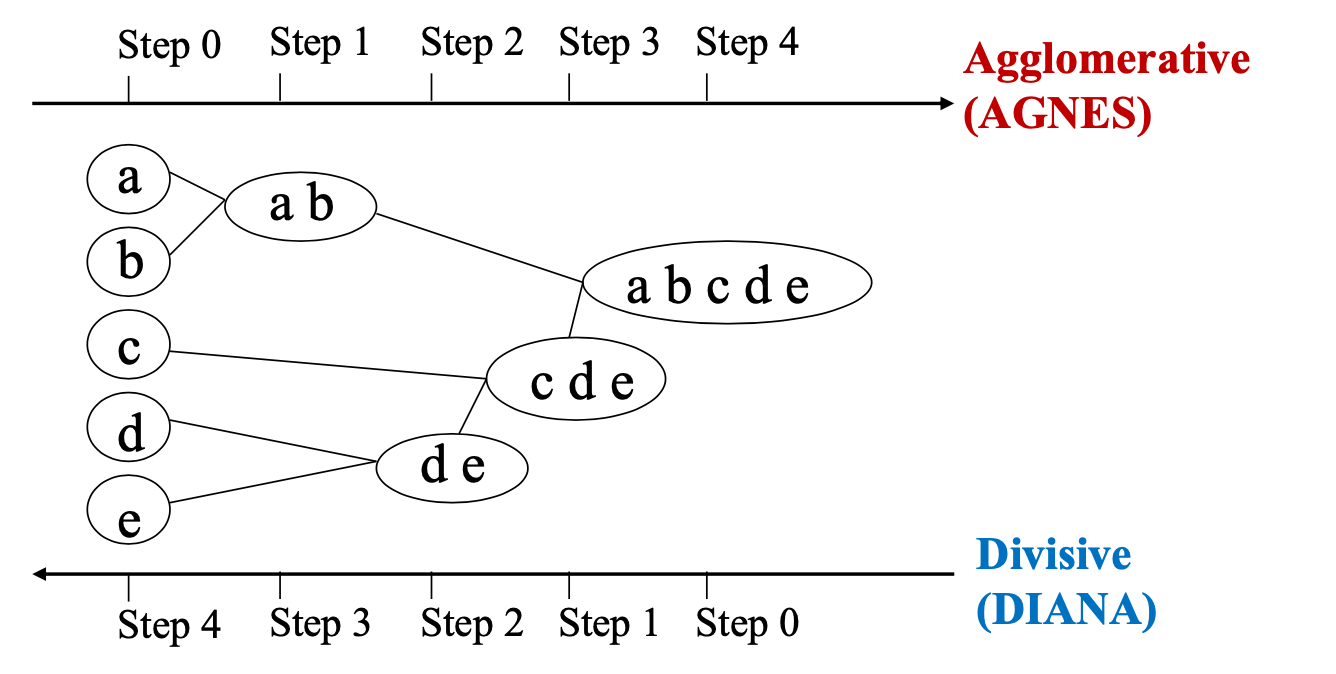
两种流行的方法: 凝聚 (ANGES) 和分裂 (DIANA) 方法

AGNES（Agglomerative Nesting）是一种自下而上的聚类方法。它从将每个数据点视为一个单独的簇开始，然后逐步合并最相似的簇，直到达到某个终止条件。
1. 开始时：每个数据点是一个单独的簇。
2. 查找最近的簇：计算所有可能的簇对之间的距离，并合并最近的两个簇。
3. 重复：继续合并簇，直到只剩下一个簇或满足某个终止条件（如达到指定的簇数量）。
DIANA（Divisive Analysis）是一种自上而下的聚类方法。它从将所有数据点视为一个单一的大簇开始，然后逐步将簇分裂成更小的簇，直到每个数据点成为一个单独的簇或达到某个终止条件。
1. 开始时：所有数据点都在一个大簇中。
2. 分裂簇：找到最合适的方法将一个簇分裂成两个更小的簇。
3. 重复：继续分裂簇，直到每个数据点都是一个单独的簇或满足某个终止条件。

树状图（Dendrogram）: 无论是凝聚还是分裂，聚类过程可以用树状图来表示。这种图表展示了每个阶段的簇是如何合并或分裂的。在树状图中，每个分支代表一个簇，分支的合并或分裂代表簇的合并或分裂过程。

距离矩阵: 这两种方法都使用距离矩阵来决定如何合并或分裂簇。距离矩阵记录了每对数据点之间的距离，这些距离用于评估簇之间的相似性或差异性。

Example

假设一个图书馆想要根据书籍的相似性对其进行分类。使用AGNES方法，每本书最初被视为一个独立的簇。然后，根据书籍的相似性（如主题、作者、出版年份等），最相似的书籍被合并成一个簇。这个过程一直进行，直到形成一个包含所有书籍的大簇，或者达到图书馆设定的分类数量。整个过程可以用树状图来表示，显示了哪些书籍首先被合并，以及随后的合并过程。

使用距离矩阵作为聚类标准。该方法不需要簇数k作为输入，但需要终止条件

凝聚聚类方法的主要弱点

扩展性不好：时间复杂度至少为 O(n^2)，其中 n 是对象总数（需要计算每对对象的相似度或相异度）
永远无法撤销之前所做的事情
即使数据包含其他形状的簇，分层方法也偏向于寻找“球形”簇。
分区是通过 "切割 "树枝图或在构成层次结构的嵌套聚类序列中选择一个解决方案来实现的。
为数据确定适当的簇数很困难。一种非正式的方法是检查树枝图中融合水平之间的差异。如果变化较大，则表示有特定数量的聚类

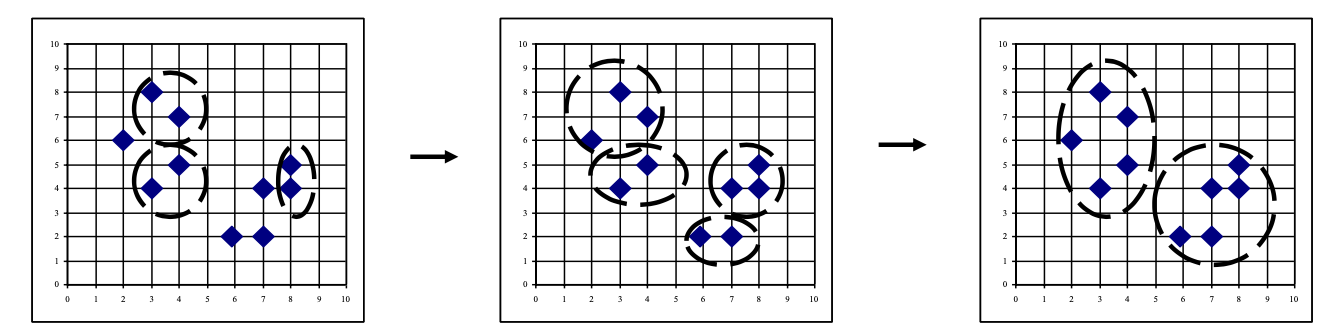
Agglomerative Nesting

Also known as nearest neighbor (1NN) technique.

Use the Single-Linkage method and the dissimilarity matrix.
Merge nodes that have the least dissimilarity.
Go on in a non-descending fashion.
Eventually all nodes belong to the same cluster

工作方式：

开始：最初，每个数据点都是一个单独的簇或“节点”。
使用不相似度矩阵：不相似度矩阵包含了每对数据点之间的不相似度（或距离）。越不相似或距离越远的点，在矩阵中的值越大。
单链路方法：这个方法在合并簇时考虑的是簇之间最近的成员。即，两个簇之间的距离定义为这两个簇中最接近的两个点之间的距离。
合并最相似的节点：在每一步，选择不相似度矩阵中具有最小不相似度（即最近距离）的两个节点合并成一个新的簇。
非降序方式：这个过程以非降序方式进行，意味着每次合并后，新形成的簇的不相似度不会低于之前任何一次合并的簇。（换句话说，随着聚类过程的进行，你会发现合并的两个簇之间的距离或不相似度会逐渐增加。）
最终合并：这个过程一直持续，直到所有的节点都合并到一个单一的大簇中。

假设有四个点A、B、C和D，不相似度矩阵可能看起来像这样：

	A	B	C	D
A	0	1.2	2.5	3.1
B	1.2	0	1.7	2.8
C	2.5	1.7	0	1.4
D	3.1	2.8	1.4	0

这个矩阵显示了每对点之间的不相似度。在AGNES的聚类过程中，会根据这个矩阵来决定哪些点应该首先被合并。例如，根据上表，点A和B之间的不相似度是最小的（1.2），因此在聚类的初始阶段，A和B可能首先被合并成一个簇。随后，聚类过程会根据更新后的不相似度矩阵继续进行，直到所有点最终合并成一个大簇。

Example

假设我们有一个关于植物的数据集，每个数据点代表一种植物，根据它们的某些特征（如高度、叶子形状等）计算出不相似度。

开始时，每种植物都是一个独立的簇。
查看不相似度矩阵，找出距离最近的两种植物，比如植物A和植物B。
将植物A和植物B合并成一个新的簇。
继续这个过程，比如下一步可能将新形成的簇（包含植物A和B）与植物C合并，因为它们之间的不相似度最小。
这个过程一直持续，直到所有植物都归为一个大簇。

通过这种方式，AGNES方法能够根据植物之间的相似性，逐步构建出一个显示植物之间关系的层次结构。

在层次聚类（如Agglomerative Nesting/Clustering）中，有几种不同的方法来定义不同群组（簇）之间的“距离”。这些方法决定了簇是如何形成和合并的。让我通俗地解释一下这些不同方法：

Single Linkage Method

Agglomerative Nesting/Clustering: Single Linkage Method

The distance between groups is defined as the closest pair of records from each group.

Example

假设距离矩阵D1。
矩阵中最小的条目是个体 1 和 2，因此它们被连接起来形成一个二成员簇。该集群与其他三个个体之间的距离重新计算为
- d(12)3 = min[d13,d23] = d23 = 5.0
- d(12)4 = min[d14,d24] = d24 = 9.0
- d(12)5 = min[d15,d25] = d25 = 8.0

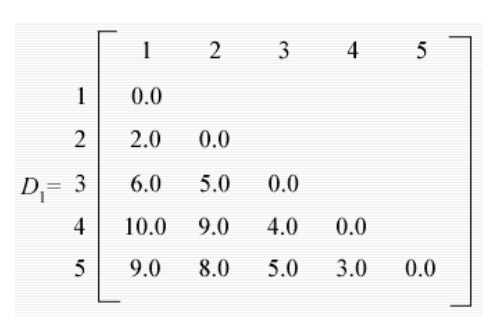
现在可以构建新的矩阵D2，其条目是个体间距离和簇个体值。

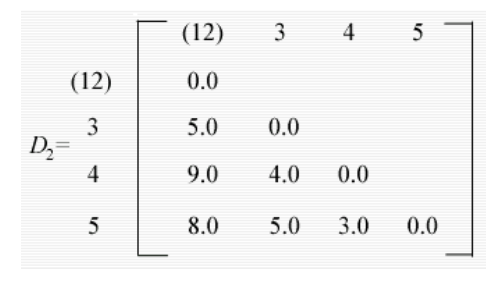
D2 中最小的条目是个体 4 和 5 的条目，因此它们现在形成第二个双成员簇，并且发现了一组新的距离
- d(12)3 = 5.0 as before
- d(12)(45) = min[d14,d15,d24,d25] = 8.0
- d(45)3 = min[d34,d35] = d34 = 4.0
These may be arranged in a matrix D3.

现在 d(45)3 中的最小条目，因此个体 3 被添加到包含个体 4 和 5 的簇中。最后，包含个体 1、2 和 3、4、5 的组被组合成单个簇。每个阶段产生的分区在右侧。

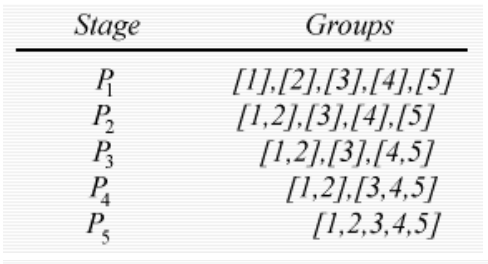
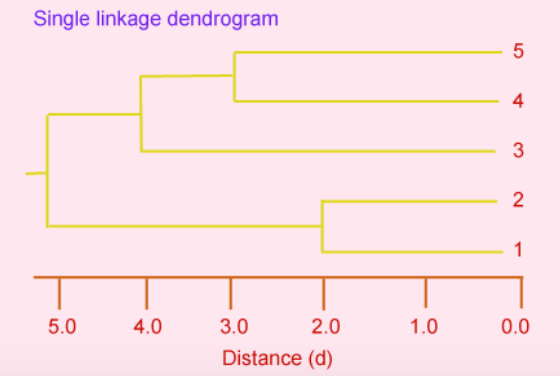
Decompose data objects into a several levels of nested partitioning (tree of clusters), called a dendrogram. 「将数据对象分解成几层嵌套分区（聚类树），称为树枝图。」
数据对象的聚类是通过在所需的层次上切割树枝图来实现的，然后每个相连的成分形成一个聚类。

Complete Linkage Method

定义：在完全链接聚类中，两个簇之间的距离定义为簇内最远的两个点之间的距离。
例子：假设有两个簇，簇A有点1和2，簇B有点3和4。如果点1和点4之间的距离是所有点对之间最远的，那么这个距离就是簇A和簇B之间的距离。

Group-average Clustering Method

定义：在群平均聚类中，两个簇之间的距离是这两个簇中所有点对之间距离的平均值。
例子：继续上面的例子，我们会计算点1到点3、点1到点4、点2到点3和点2到点4这四对点之间的距离，然后取这些距离的平均值作为簇A和簇B之间的距离。

Centroid Clustering Method

定义：在质心聚类中，每个簇由其所有点的平均值（或质心）代表。两个簇之间的距离是它们的质心之间的距离。
例子：假设簇A的质心是点1和点2坐标的平均值，簇B的质心是点3和点4坐标的平均值。那么簇A和簇B之间的距离就是这两个质心之间的距离。

这些不同的方法影响着聚类的最终结果。例如，

完全链接聚类倾向于产生更加紧密和均匀大小的簇，因为它避免了将距离较远的点合并到同一个簇中。
而群平均聚类提供了一种平衡的方法，既考虑了簇内的紧密程度，也考虑了簇的整体大小。
质心聚类则侧重于簇中点的整体“中心”位置。

Divisive Analysis

Clustering

# Clustering

# General Applications

# Good Clustering

# Data Structures

# Data matrix

# Dissimilarity matrix

# Distance Measure

# Objects

# Binary Variables

# Nominal/Categorical Variables

# 方法一：简单搭配

# 方法2：使用大量二进制变量

# Transactional Data

# Major Clustering Approach

# Partitioning Algorithms

# K-Means Clustering Method

# K-Medoids Clustering Method

# Hierarchical Clustering

# Agglomerative Nesting

# Single Linkage Method

# Complete Linkage Method

# Group-average Clustering Method

# Centroid Clustering Method

# Divisive Analysis

Clustering

General Applications

Good Clustering

Data Structures

Data matrix

Dissimilarity matrix

Distance Measure

Objects

Binary Variables

Nominal/Categorical Variables

方法一：简单搭配

方法2：使用大量二进制变量

Transactional Data

Major Clustering Approach

Partitioning Algorithms

K-Means Clustering Method

K-Medoids Clustering Method

Hierarchical Clustering

Agglomerative Nesting

Single Linkage Method

Complete Linkage Method

Group-average Clustering Method

Centroid Clustering Method

Divisive Analysis