Regression Trees

Regression Trees or Classification and Regression Tree (CART)

分类树用于处理离散的标签（如是/否、狗/猫），而回归树处理的是连续的数值（如房价、温度）。

Similarity

• 用于连续结果变量
• 程序类似于分类树
• 尝试多次拆分，选择杂质最小的一次

Difference

• 预测结果按相关分支/规则的数字目标变量的平均值计算（参照决策树中的多数表决）。
• 杂质用与叶平均值的平方差之和来衡量
• 用 RMSE（均方根误差）衡量性能

Regression Tree -> Decision Tree for Regression

Construction

1. 选择最佳分割点：在回归树中，我们使用不同的标准，通常是偏差减少（Deviation Reduction）。这意味着我们要找到一个特征和一个分割点，使得分割后的两个子集相对于原始数据集的总偏差（差异）最小化。
2. 偏差减少的计算
   • 偏差通常通过计算每个点与其所在组的平均值的差的平方来衡量。
   • 我们尝试不同的特征和分割点，计算每种情况下的总偏差，并选择使总偏差最小的分割。
3. 递归分割：
   • 一旦找到最佳分割点，数据集被分为两个子集。
   • 然后对每个子集重复这个过程，直到满足某个停止条件（如达到最大深度、子集大小低于阈值等）
4. 预测输出：回归树的每个叶节点会得到一个预测值，这通常是该节点所有数据点的平均值。

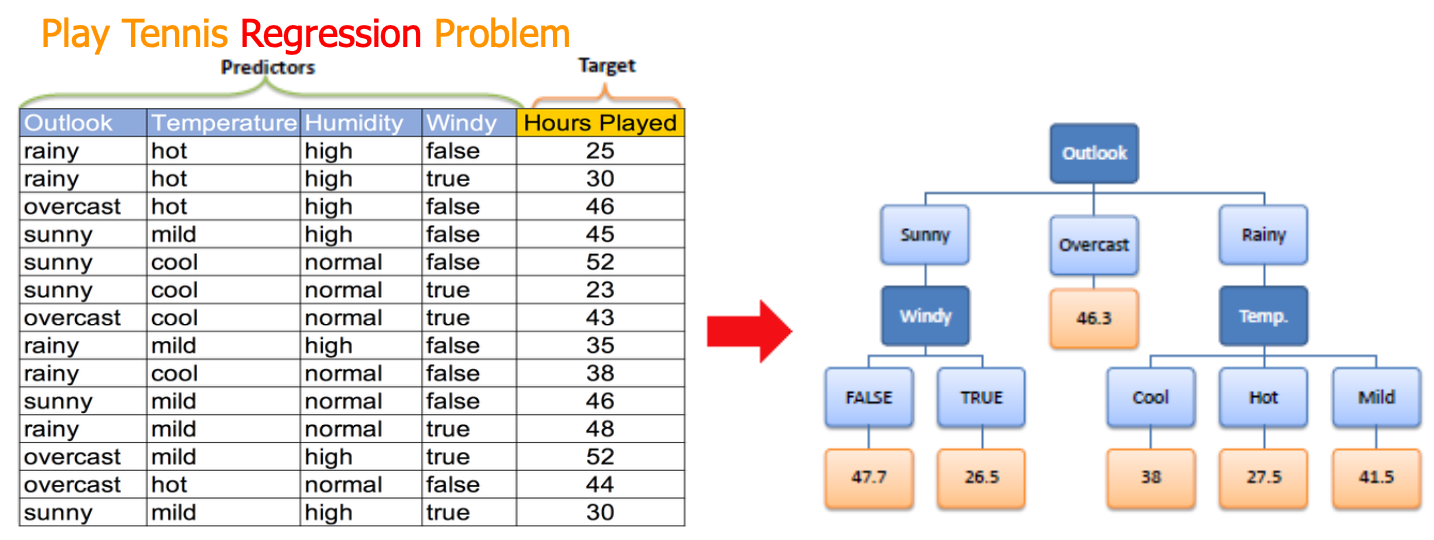
Example

假设我们有一个数据集，包含不同房屋的特征（如面积、卧室数量）和它们的售价（一个连续值）。我们的目标是构建一个回归树来预测房价。

• 我们可能会检查不同的特征（面积、卧室数量）和不同的分割点（面积>100平方米、卧室数量>3等）。
• 对于每种可能的分割，我们计算分割后两个子集中每个房子的售价与其所在子集平均售价的偏差。
• 我们选择那个能使总偏差最小的分割点。比如，我们可能发现按照面积分割时偏差最小。
• 然后，我们在每个子集中重复这个过程，直到达到停止条件。

最终，我们得到的回归树可以根据房屋的特征来预测其可能的售价。每个叶节点代表的是在那个特定条件下的房屋的平均售价。

Deviation Reduction

在回归树中，我们用一些统计度量来帮助我们构建树（分枝）以及决定何时停止分枝（终止分枝）。这个过程和计算均值、标准差和变异系数（CV）类似。

• 标准差（S）：用于树的构建（分枝）
  • 标准差是衡量数据点相对于平均值的离散程度的一个指标。
  • 在回归树中，我们使用标准差来找到最好的分枝点。选择一个分枝点会将数据分成两部分，我们希望这两部分内部的标准差尽可能小，这意味着每个子组内的数据更加相似。
• 变异系数（CV, Coeffeicient of Variation）：用于确定分枝何时终止
  • 变异系数是标准差与平均值的比率，通常表示为百分比。
  • 在回归树中，如果一个节点的CV很小，意味着该节点内的数据变异不大，我们可能就不需要进一步分枝了。
• 平均值（Avg）：是叶节点中的值
  • 在决定不再分枝后，叶节点将代表该分支上数据的平均值。
  • 对于预测任务，这个平均值就是我们基于输入数据预测的连续输出（比如房价、体重等）。

Standard deviation for two attributes

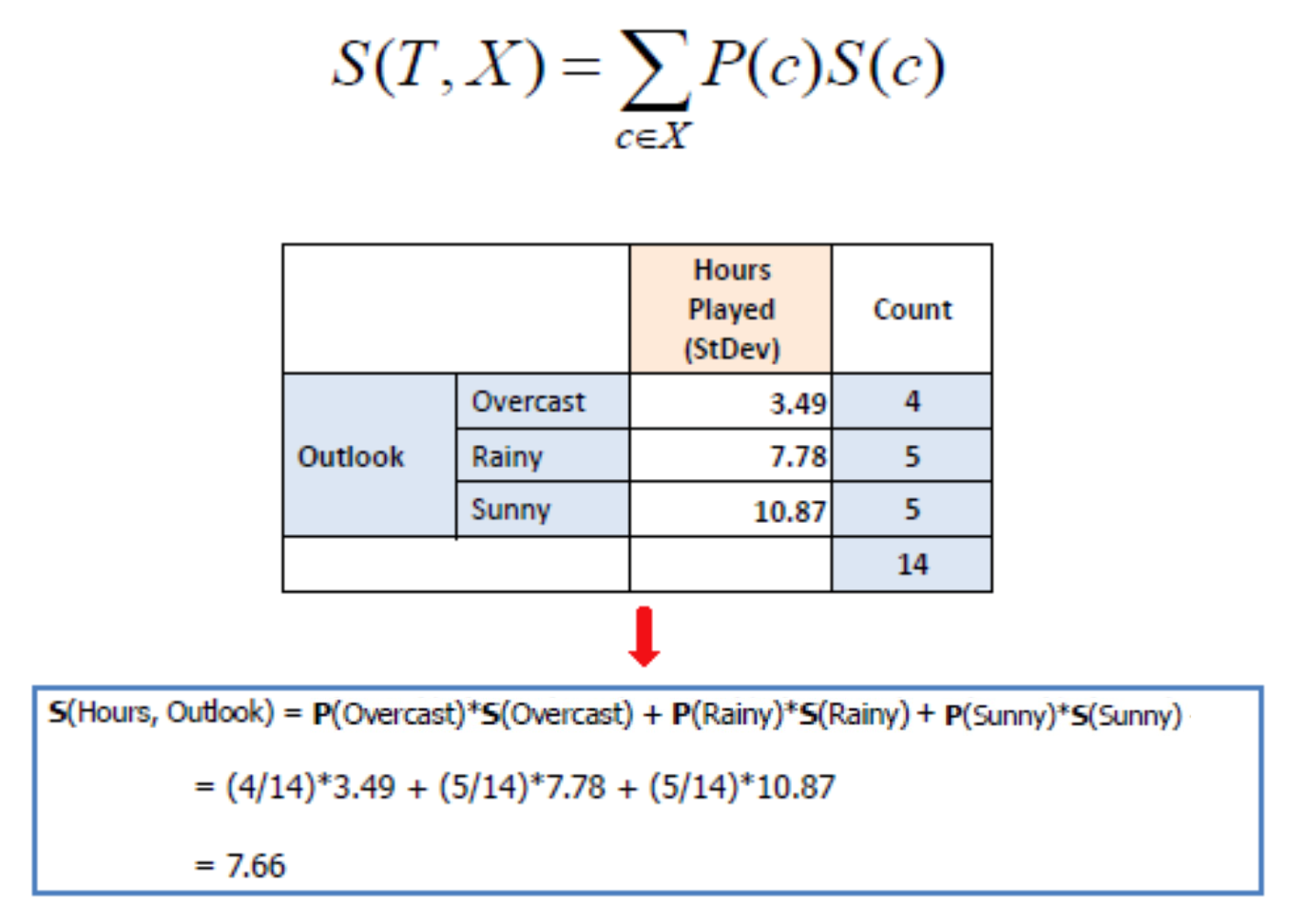
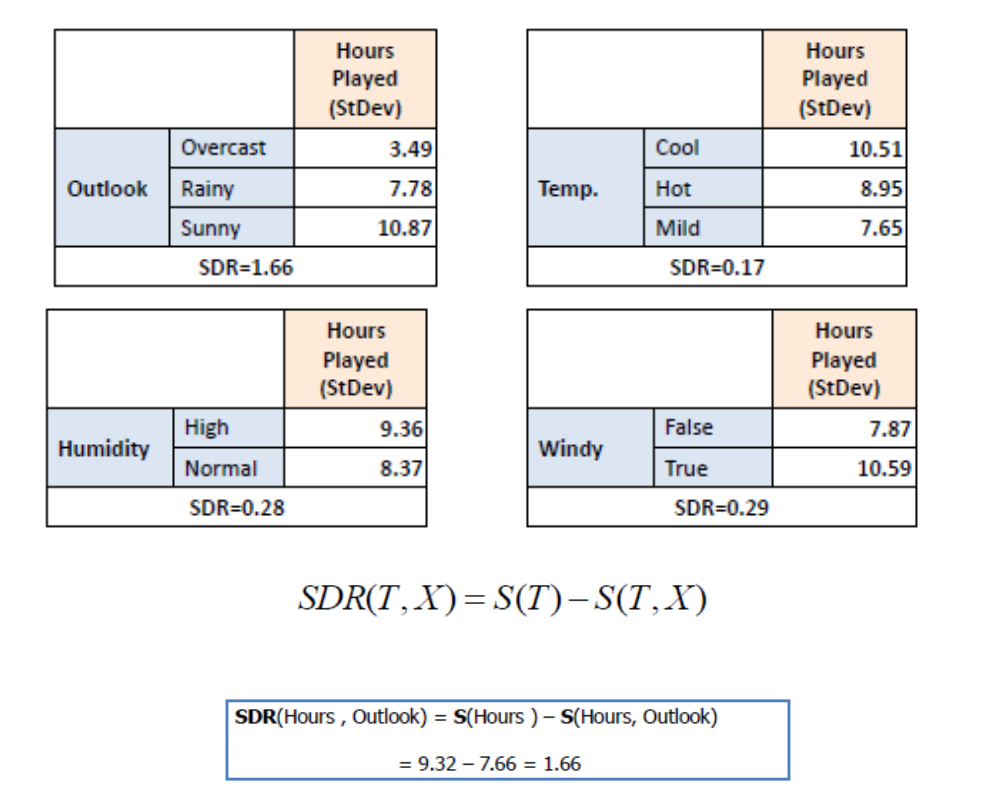
Standard Deviation Reduction

Calculate the standard deviation for each branch

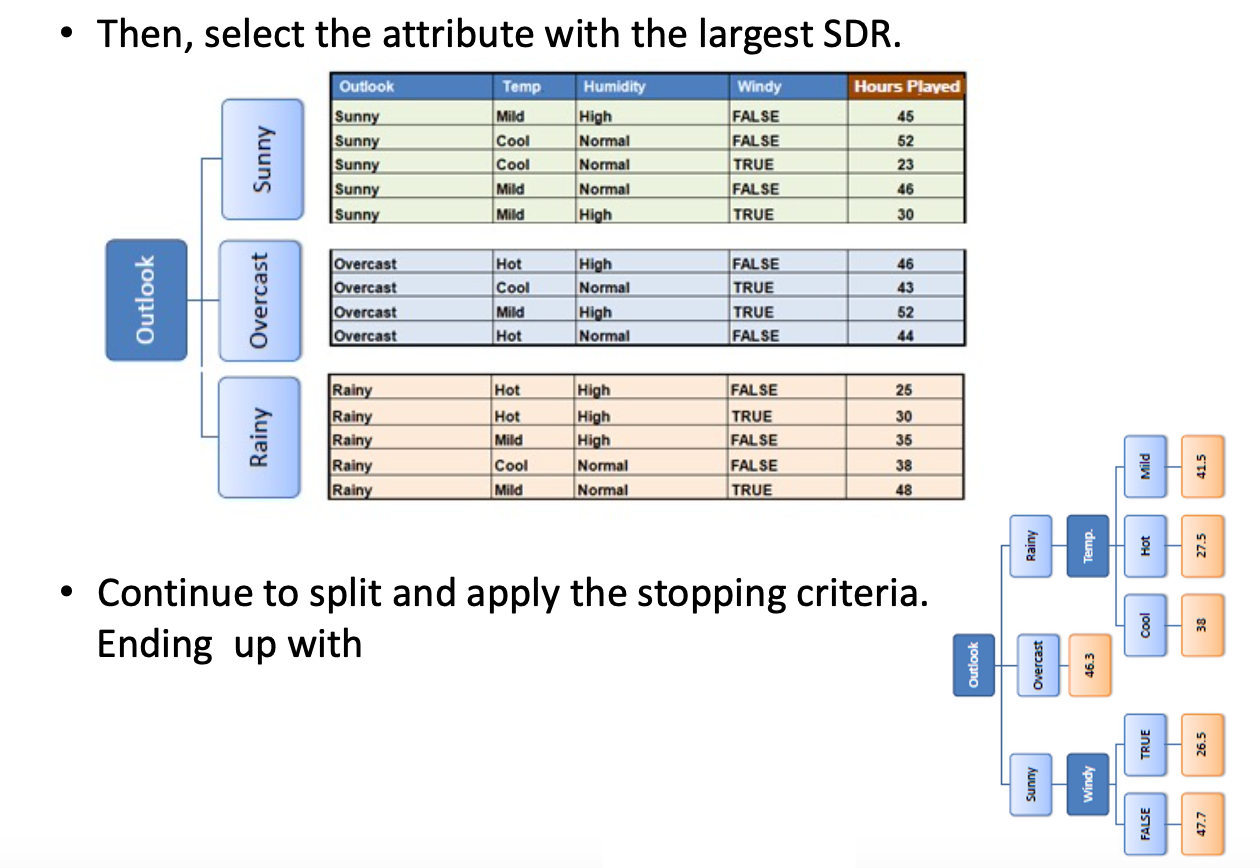
Constructing Tree

Constructing Regression Tree Based on SDR