跳至主要內容

Decision Tree for Classification

Hirsun大约 33 分钟

Decision Tree for Classification

Two-Step Process

Model construction: describing a set of predetermined classes

  • 模型构建：描述一组预定的类
  • 模型用途：对未来或未知对象进行分类
Classification vs. Prediction

Classification

  • predicts categorical class labels
  • 根据训练集和分类属性中的值（类别标签）对数据进行分类（构建模型），并用于对新数据进行分类

Prediction

  • 建立连续值函数模型，即预测未知值或缺失值
  • eg. predicting the house price
  • Also referred as regression

Typical Applications

  • credit approval
  • target marketing
  • medical diagnosis
  • Price prediction

Issues

Data Preparation

  • 数据清理: 预处理数据以减少噪音并处理缺失值
  • Relevance analysis（特征选择）: 删除不相关或冗余的属性
  • Data transformation: 概括「Generalize」和/或 标准化「normalize」 数据

Method Evalution

  • Predictive accuracy
  • Speed and scalability
    • time to construct the model
    • time to use the model
  • Robustness: handling noise and missing values
  • Scalability: efficiency in disk-resident databases
  • Interpretability「可解释性」: understanding and insight provided by the model
  • Goodness of rules
    • decision tree size
    • compactness of classification rules 「分类规则的紧凑性」

Decision Tree Induction

决策树结构

  • 类似流程图的树形结构
  • 内部节点表示对属性的测试
  • 分支代表测试的结果
  • 叶节点代表类别标签或类别分布

决策树生成由两个阶段组成

  • Tree construction
    • 一开始，所有训练示例都位于根目录
    • 基于所选属性递归划分示例
  • Tree pruning「修剪」：识别并删除反映噪音或异常值的分支

决策树的用途：对未知样本进行分类，根据决策树测试样本的属性值

CleanShot 2023-11-20 at 00.23.15@2x.png
CleanShot 2023-11-20 at 00.23.15@2x.png

Extracting Rules from Trees

  • 以 IF-THEN 规则的形式表示知识
  • 为从根到叶的每条路径创建一条规则
  • 路径上的每个属性-值对形成一个合取
  • 叶节点保存类别预测
  • 规则更容易让人理解
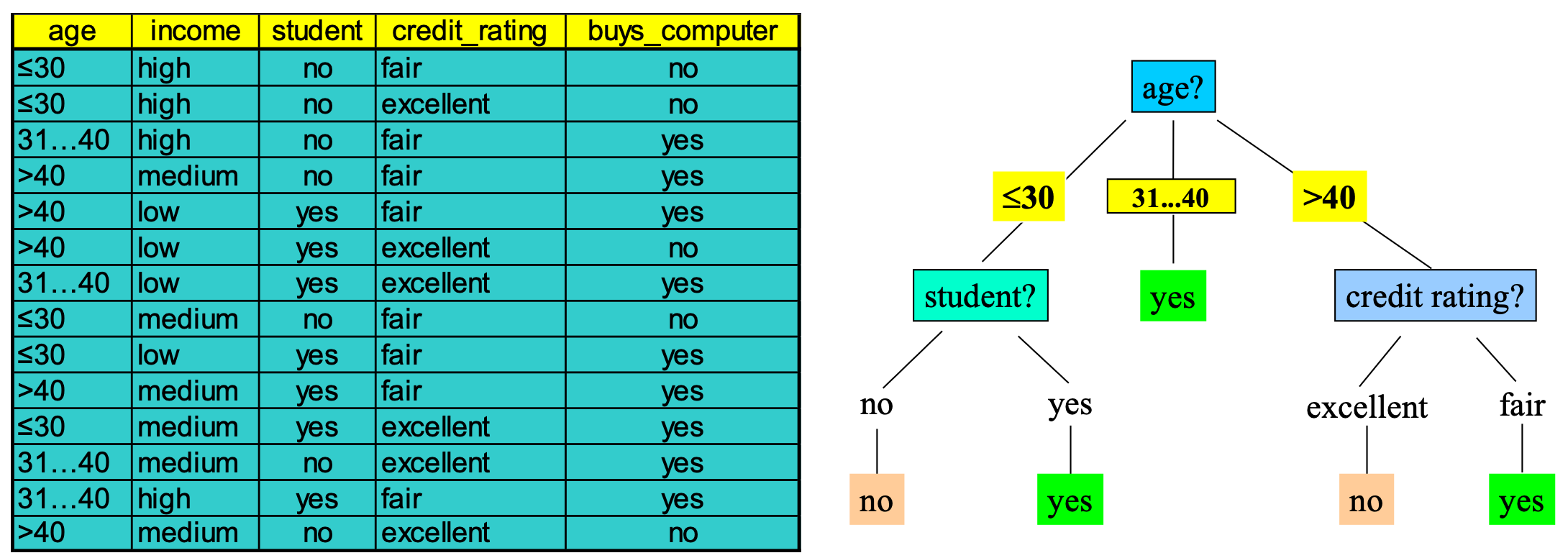
Example

IF age = “≤30” AND student = “no” THEN buys_computer = “no”
IF age = “≤ 30” AND student = “yes” THEN buys_computer = “yes”
IF age = “31...40” THEN buys_computer = “yes”
IF age = “>40” AND credit_rating = “excellent” THEN buys_computer = “no” 
IF age = “>40” AND credit_rating = “fair” THEN buys_computer = “yes”

Tree Construction Algorithm

基本算法（贪心「Greedy」算法）

  • 树以自顶向下递归分而治之的方式构建
  • 一开始，所有训练示例都位于根目录
  • 属性是分类的（如果是连续值，则提前离散化）
  • 根据所选属性对示例进行递归分区
  • 根据启发式方法或统计方法（如信息增益）选择测试属性

停止分区「partitioning」的条件

  • 给定节点的所有样本都属于同一类
  • 没有剩余的属性可供进一步划分 - 采用多数投票法对叶片进行分类
  • There are no samples left

Attribute Selection Measure

在决策树算法中，选择哪个属性作为节点来分割数据是非常重要的。为了做出这个选择，我们使用一些度量来评估不同属性的有效性。这里，我们讨论的两个度量是信息增益和基尼指数。

Information Gain

「信息增益」(ID3/C4.5)

  • 用来选择哪个特征最适合作为当前节点的分割依据。
  • 应用：通常用于分类属性，但也可以修改以适用于连续值属性。
  • 基本思想：信息增益度量了选择一个属性作为决策点（节点）后，数据不确定性减少的程度。更高的信息增益意味着更少的不确定性。
  • 计算方式：通过计算数据集的熵（一种度量数据混乱程度的指标）和分割后各个子集的熵来计算。

注意

  • 信息增益（Information Gain）是一个差值，它用来衡量在使用某个特征（或属性）来分割数据集之后，数据不确定性（熵）减少了多少。
  • 计算信息增益： 信息增益 = 初始熵 − 分割后的熵。

Entropy

信息熵（Entropy）是一个数学概念，

  • 用于衡量数据集的混乱程度或不确定性。
  • 它的计算基于数据集中各种结果的概率。
  • 在一个完全不确定的系统中，信息熵是最高的；
  • 而在一个完全确定的系统中，信息熵则为零。

在决策树中，

  • 一个高熵的数据集表明它包含了许多不同类别的数据，这些数据很难基于当前的属性进行有效区分。
  • 相反，低熵意味着数据集中的大多数数据都属于同一个类别，更容易区分。

总结来说，信息熵是一个度量数据集不确定性的指标。在构建决策树时，我们通常寻找能最大程度降低熵的属性，也就是说，找到能最清晰地划分数据集的属性。

Example

想象一个简单的例子，一个班级的学生分为戴眼镜和不戴眼镜两类。如果班级里几乎所有学生都戴眼镜，那么这个数据集的熵就很低，因为几乎所有的学生都可以用同一个标签（戴眼镜）来描述。但如果班级里戴眼镜和不戴眼镜的学生数量几乎相等，那么这个数据集的熵就很高，因为单凭是否戴眼镜这个属性很难区分学生。

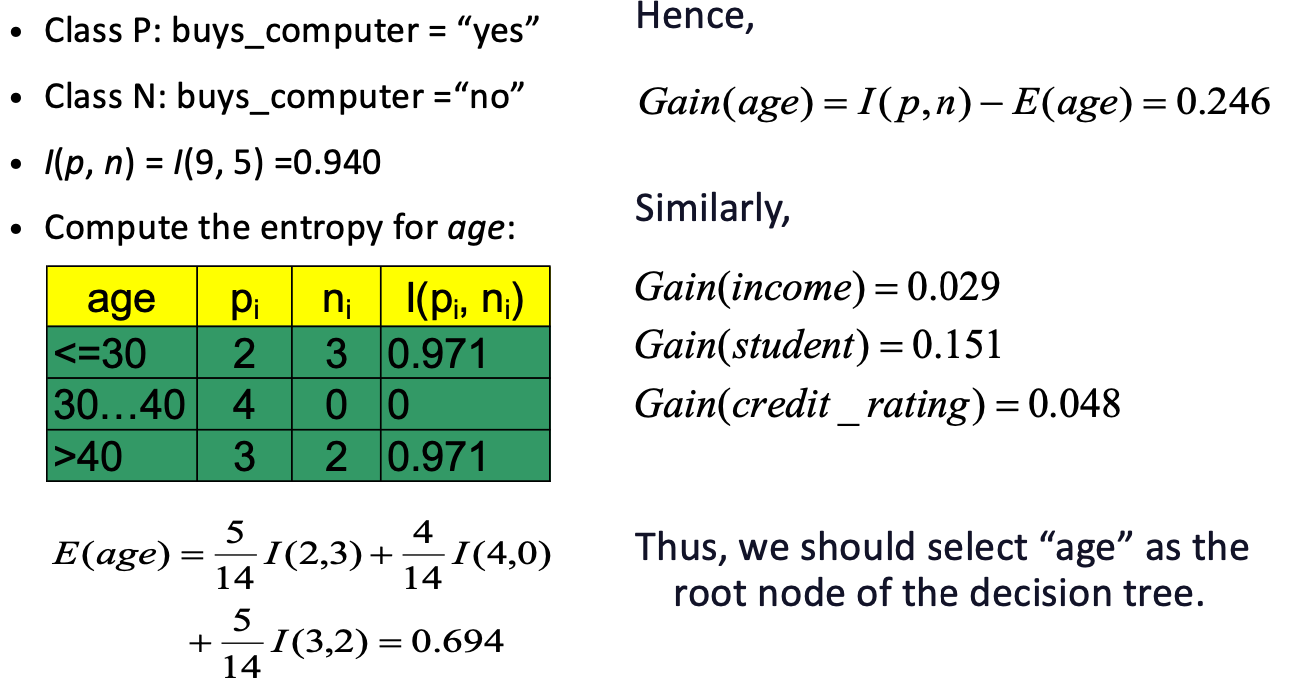
Initial Entropy

Select the attribute with the highest information gain 「选择信息增益最高的属性」

假设有两个类，P和N

  • 令样本集 S , 包含 P 类的 p 个元素和 N 类的 n 个元素
  • 决定 S 中的任意示例属于 P 还是 N 所需的信息量 定义为

I(p,n)=−pp+nlog⁡2pp+n−np+nlog⁡2np+n I(p, n)=-\frac{p}{p+n} \log _{2} \frac{p}{p+n}-\frac{n}{p+n} \log _{2} \frac{n}{p+n}

Example

假设你有一个包含动物的数据集，你想分类它们是猫（P类）还是狗（N类）。如果你的数据集中有9只猫和1只狗，那么我们可以用这个公式来计算这个数据集的熵。

  • 猫（P类）的比例是 910\frac{9}{10}（因为有9只猫和10只动物总计），狗（N类）的比例是 110\frac{1}{10}。
  • 将这些比例代入公式，我们得到 I(9,1)。这个值告诉我们，根据猫和狗的分布，我们需要多少信息来确定一个随机选取的动物是猫还是狗。
1700451383749.png

Entropy after Segmentation

假设使用属性 A 将集合 S 划分为集合 {S1、S2 , ..., Sv}

如果 Si 包含 P 的 pi 个示例和 N 的 ni 个示例，则对所有子树 Si 中的对象进行分类所需的熵或预期信息为

E(A)=∑i=1vpi+nip+nI(pi,ni) E(A)=\sum_{i=1}^{v} \frac{p_{i}+n_{i}}{p+n} I\left(p_{i}, n_{i}\right)

信息增益： Gain(A) = I(p, n) - E(A)

注意

  • 信息熵的值是正数。
  • 学习算法中，信息增益值 Gain(A) 是正数。
  • Gain(A) 越大，数据集的不确定性减少地越多，我们的不确定性就变得越少。
Example

假设我们有一个数据集，它关于学生是否喜欢数学（是或否）。我们想要根据他们是否参加体育活动（是或否）来分割这个数据集。

我们的目标是计算使用“是否参加体育活动”这个属性作为分割点的预期信息 E(A)。

  • 总共有10个学生。
  • 6个学生参加体育活动，其中4个喜欢数学（P类），2个不喜欢数学（N类）。
  • 4个学生不参加体育活动，其中1个喜欢数学，3个不喜欢数学。

根据这些信息，我们可以计算每个子集的熵，并加权求和以得到预期信息 E(A)。

  1. 计算子集 S1（参加体育活动的学生）的熵：
    • p1=4（喜欢数学的学生数）
    • n1=2（不喜欢数学的学生数）
    • I(p1,n1)=−46log⁡246−26log⁡226I(p_1, n_1) = -\frac{4}{6} \log_2 \frac{4}{6} - \frac{2}{6} \log_2 \frac{2}{6}
  2. 计算子集 S2（不参加体育活动的学生）的熵：
    • p2=1
    • n2=3
    • I(p2,n2)=−14log⁡214−34log⁡234I(p_2, n_2) = -\frac{1}{4} \log_2 \frac{1}{4} - \frac{3}{4} \log_2 \frac{3}{4}
  3. 计算预期信息 E(A)
    • E(A)=610I(p1,n1)+410I(p2,n2)E(A) = \frac{6}{10} I(p_1, n_1) + \frac{4}{10} I(p_2, n_2)

Attribute Selection

1700451822006.png
Thinking time

Q1.能否在 buys_computer 数据集中再添加一条记录，使训练集的分类准确率低于 100%？

可以添加一条与现有数据冲突或不一致的记录。这种记录应该在特征上与某个类别的其他记录相似，但在标签（类别）上不同。这样的记录会引入一个异常点或噪声，使得决策树无法再完美地对所有训练数据进行分类。

如，假设 buys_computer 数据集是基于属性如年龄、收入、学历和信用等来预测某人是否会购买电脑。如果所有的高收入、高学历和良好信用的人在训练集中都标记为会购买电脑，那么你可以添加一条记录，其中这个人有高收入、高学历和良好信用，但标记为不会购买电脑。这会让决策树在这个特定的数据点上犯错，从而降低其在训练集上的准确率。

Q2. 当一个给定的训练数据集无法被决策树完美分类时，有几种策略可以用来提高其性能

当一个给定的训练数据集无法被决策树完美分类时，有几种策略可以用来提高其性能：

  1. 数据预处理：
    • 清洗数据：移除或纠正错误和异常值。
    • 特征工程：创建新的特征或转换现有特征来提高它们的预测能力。
    • 标准化或归一化数据：尤其是当数据特征在量级上有很大差异时。
  2. 优化决策树参数：
    • 调整树的深度：限制树的深度可以防止过拟合。
    • 调整节点分裂标准：例如，更改最小样本数或信息增益的阈值。
    • 剪枝：在树完全生长后，移除对最终分类影响不大的部分。
  3. 集成方法：
    • 随机森林：创建多个决策树并取它们的平均预测或多数投票结果。
    • 提升方法（如AdaBoost, Gradient Boosting）：通过顺序地增加对之前分类错误的样本的关注来构建多个决策树。
  4. 处理不平衡数据集：
    • 重采样：对少数类进行过采样或对多数类进行欠采样。
    • 使用合成数据生成技术：如SMOTE（合成少数过采样技术）。
  5. 尝试不同的决策树算法：比如C4.5、CART等，它们在处理特定类型的数据时可能比ID3算法更有效。
  6. 交叉验证：使用交叉验证来评估模型的泛化能力，并基于这些结果调整模型参数。
  7. 分析特征的重要性：识别并专注于那些对预测结果影响最大的特征。
  8. 域知识应用：结合特定领域的知识来改进特征选择和数据预处理。

In Large Databases

  • 分类 - 统计学家和机器学习研究人员广泛研究的经典问题
  • 可扩展性：以合理的速度对具有数百万个示例和数百个属性的数据集进行分类
  • 为什么要在数据挖掘中进行决策树归纳？
    • 学习速度相对较快（比其他分类方法）
    • 可转换为简单易懂的分类规则
    • 可以使用 SQL 查询来访问数据库
    • 与其他方法相当的分类精度

Gini Index

「基尼指数」

(IBM IntelligentMiner)

基本思想：基尼指数是一种衡量数据纯度的方法。较低的基尼指数表示数据较为纯净，即某一类别的数据占主导地位。

  • 假设每个属性都存在多个可能的分割值
  • 可能需要其他工具（如聚类）来获取可能的分割值
  • 应用：通常用于连续值属性，但也可以修改以适用于分类属性。

考虑一个根据房屋特征（如面积、价格）预测房屋是否会被快速出售的数据集。基尼指数会评估使用面积或价格作为分割点时，数据集中关于房屋是否快速出售的“纯度”（即一侧主要是快速出售，另一侧则不是）。

Avoid Overfitting

生成的树可能过度拟合训练数据

  • 分支过多，其中一些可能反映了噪音或异常值导致的异常情况

  • 导致未见样本的准确率较低

避免过度拟合的两种方法

  • 预剪枝：尽早停止树构建 - 如果这会导致 goodness measure 低于阈值，则不要分割节点 - 难以选择合适的阈值
  • 后期修剪：从 "完全长成 "的树上移除树枝--得到一个逐步修剪的树木序列
  • 使用一组与训练数据不同的数据来决定哪棵树是 "最佳修剪树"。
Legends never die.
Copyright © 2024 Hirsun