跳至主要內容

Spatial Clustering

Hirsun大约 26 分钟

Spatial Clustering

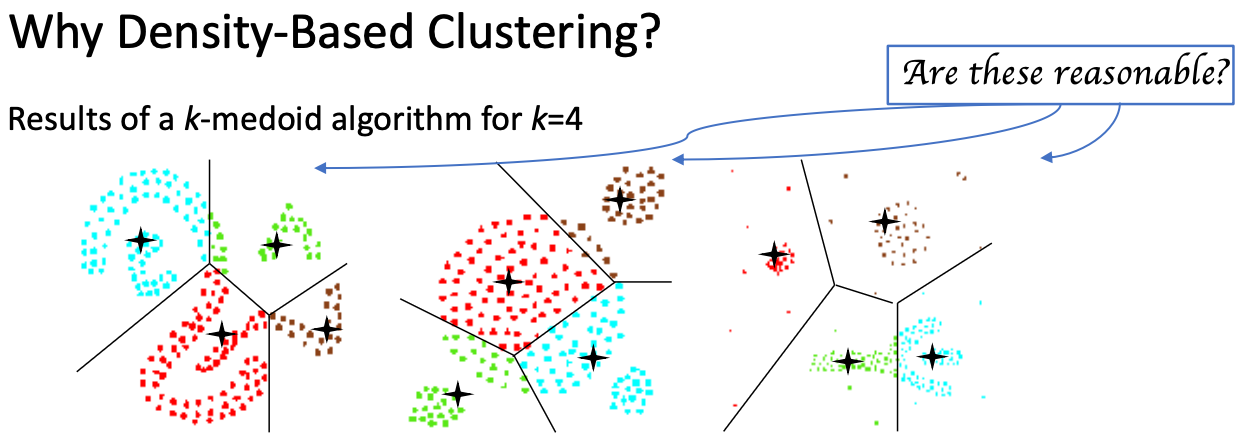
Why Density-Based Clustering methods「基于密度的聚类方法」?

  • 发现任意形状的簇
  • 簇「cluster」 – 物体密集区域被低密度区域分隔开来

DBSCAN – the first density based clustering

DBSCAN -> Density Based Spatial Clustering of Applications with Noise 「基于密度的噪声应用空间聚类」

  • 基于密度的集群概念：这意味着数据点被分组（或聚集）在一起基于它们的“密度”，即数据点的紧密程度。想象一下，你有很多点散布在一张纸上，那些彼此靠近的点会形成一个“群体”或集群。
  • 集群被定义为密度连接点的最大集合：在这里，“集群”是指一群彼此靠得很近的点。所谓“密度连接”，就是指一个点的周围有足够多的其他点，使得它们可以被视为一个单一的组或集群。
  • 在有噪声的空间数据库中发现任意形状的集群：这表明这种方法能够在包含许多随机分布（即“噪声”）的数据中找到集群，而且这些集群可以是任何形状的，不仅仅是圆形或椭圆形。
1700472279847.png

Density Based Clustering

基本思想形式化的直觉：

  • 对于簇中的任何点，该点周围的局部点密度必须超过某个阈值
  • 一个群组的点集在空间上是相连的

由两个参数定义的点 p 处的局部点密度

  • ε - 点 p 附近的半径: Nε(p):={q in data set D∣dist⁡(p,q)≤ε}N_{\varepsilon}(p):=\{q \text { in data set } D \mid \operatorname{dist}(p, q) \leq \varepsilon\}， like 圆的半径就是ε
  • MinPts - 给定邻域中的最小点数 N(p) 【至少需要有多少个点，个区域才能被认为是“密集”的，从而形成一个集群。】
Example

假设你在一个海滩上放飞无人机，无人机的相机可以看到下面的人。你要用这个无人机来找出海滩上的热门区域。

使用ε，你设置了无人机相机的焦距，定义了它能清晰看到地面上的一个特定大小的区域。比如说，你把焦距设置得能看到直径为10米的圆形区域。

接下来，你决定至少要在这个10米直径的圆形区域内看到15个人，这个区域才算是热门的。这个“15”就是你的MinPts。

现在，无人机飞过海滩，每次都在地面上标记出一个10米的圆形区域，并数里面的人。如果一个圆形区域内有15个或更多的人，那么这个区域就被标记为热门区域，或者说是一个“集群”。如果人少于15个，那么这个区域就被忽略了，因为它没有达到你设置的密集标准。通过这种方式，无人机可以帮你找到海滩上所有的热门区域。

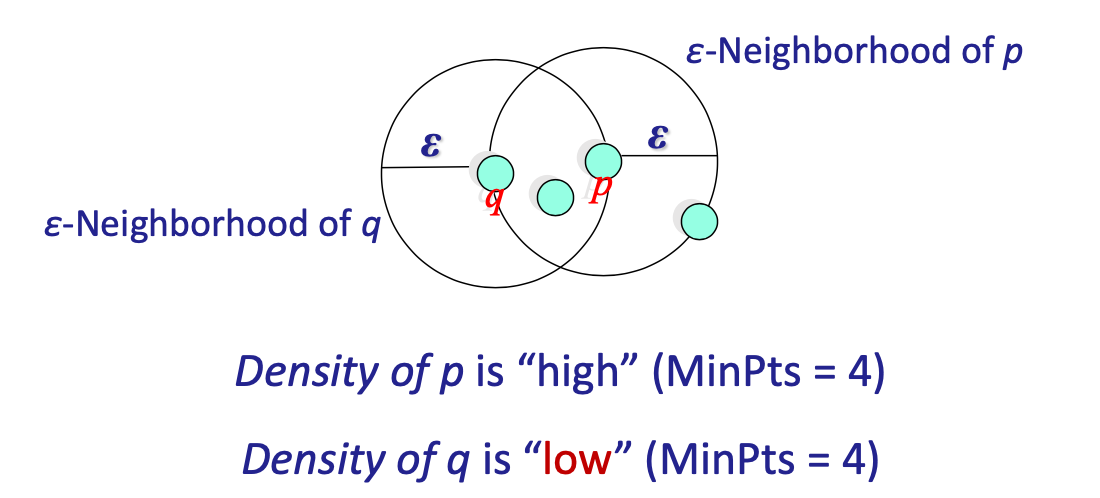
ε-Neighborhood

ε-Neighborhood: 距物体 ε 半径内的物体。

Nε(p):={q in data set D∣dist⁡(p,q)≤ε} N_{\varepsilon}(p):=\{q \text { in data set } D \mid \operatorname{dist}(p, q) \leq \varepsilon\}

“高密度”- 对象的 ε-Neighborhood 至少包含 MinPts 个对象。

1700474737732.png

MinPts

ε-Neighborhood 至少包含 MinPts 个对象，计数包含中心本身。

Core, Border & Outlier

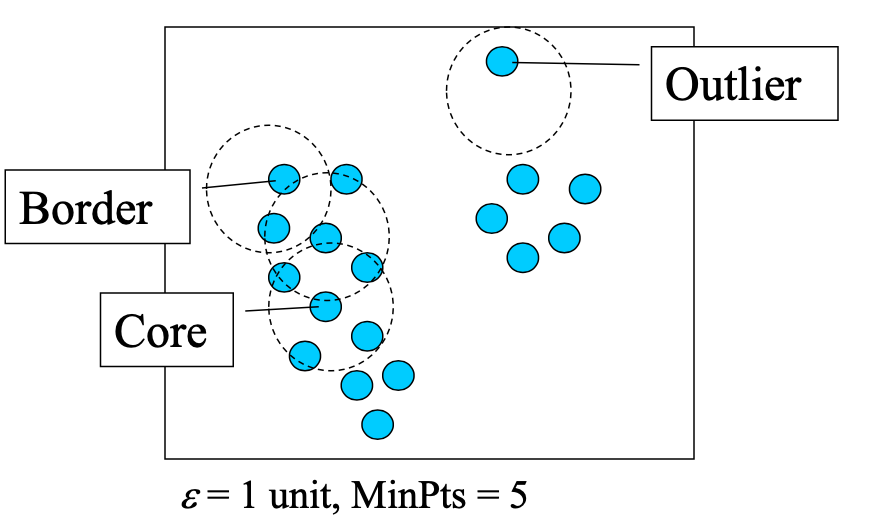
给定 ε 和 MinPts，我们可以将对象分为三个不同的组。

  • 如果一个点在 Eps 范围内的点数（MinPts）超过指定数量，则该点为 core point。这些点位于群集的内部。
  • border point 在 Eps 范围内的最小点数少于 MinPts，但位于核心点附近。
  • noise point/outlier 是指任何既不是核心点也不是边界点的点。
1700476026016.png

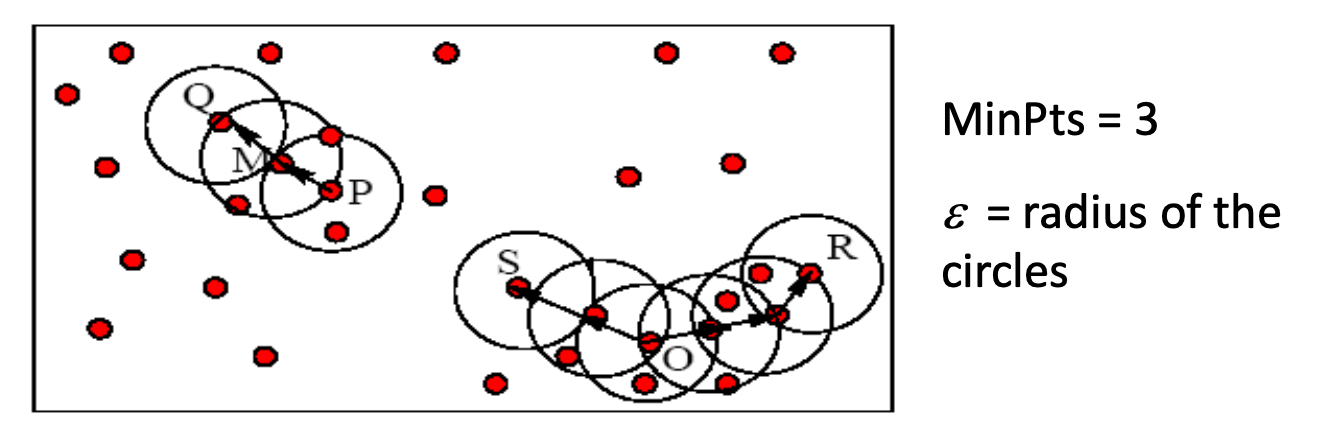
在下面的 Example, M、P、O 和 R 是core point（在 Q、M、P、S、O、R 中），因为它们每个都位于包含至少 3 个点的 ε-Neighborhood 中

1700476237789.png

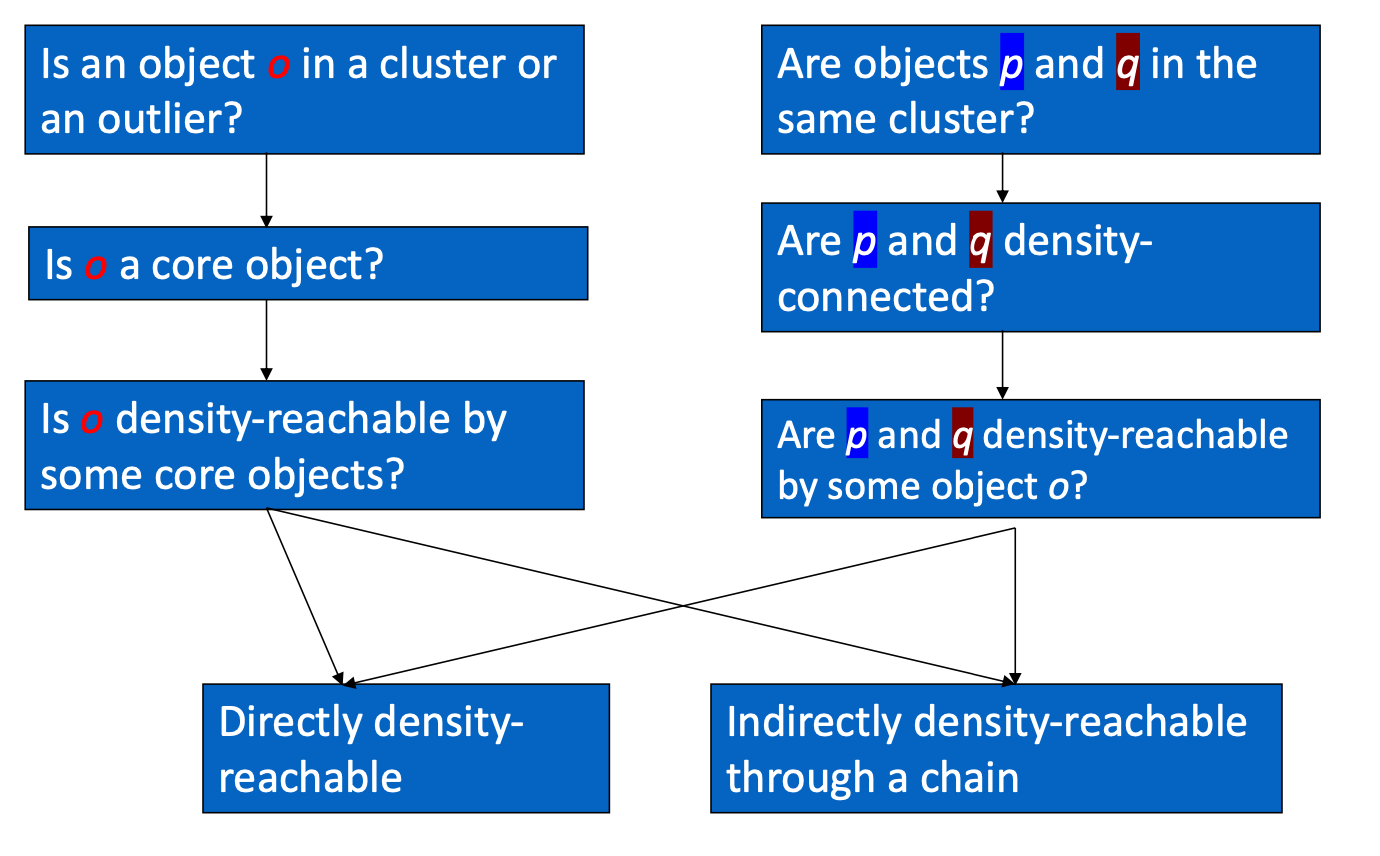
Density Reachability

Directly Density-Reachable

  • 如果 p 是核心对象，
  • 且 q 位于 p 的 ε-Neighborhood 中，

则object q is directly density-reachable from object p

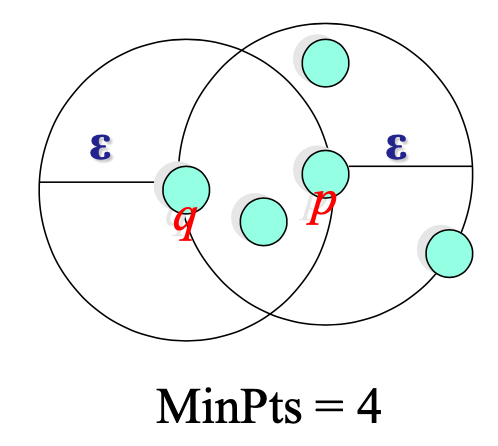
1700477634996.png

特别注意

是两个条件都要成立，而且

  • q 是从 p 直接密度可达的
  • p 不是从 q 直接密度可达的
  • 密度可达性是不对称的

Indirectly Density-Reachable

  • p 是从p2 直接密度可达的；
  • p2 是从p1 直接密度可达的；
  • p1 是从 q 直接密度可达的；

p <- p2 <- p1 <- q 形成一条链

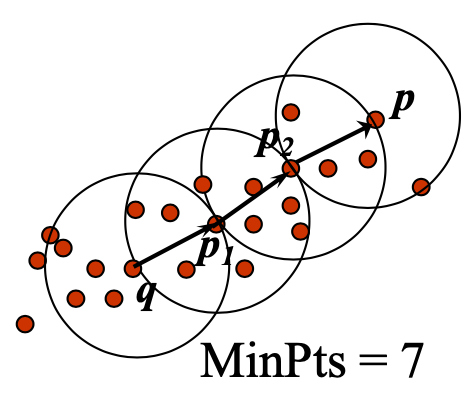
1700477977891.png

p is (indirectly) density-reachable from q

Density-Connectivity

  • Density-Reachable is not symmetric, not good enough to describe clusters.
  • Density-Connected: 如果一对点 p 和 q 从点 o 密度可达，则它们是密度连通的。
    • 密度连通性是对称的
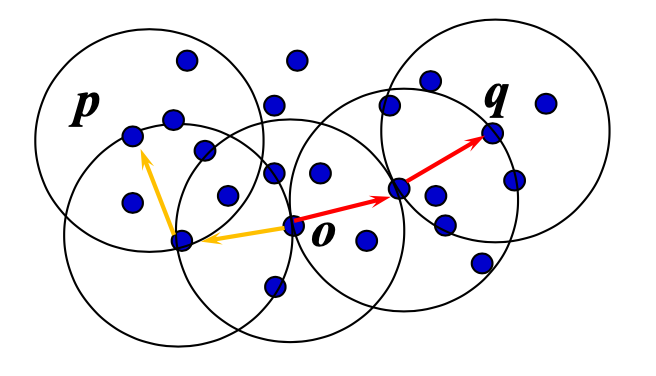
1700478156708.png

Formal Description of Cluster

  • Given a data set D, parameter ε and threshold MinPts.
  • 集群 C 是满足下面三个标准的对象子集（具有核心点和边界点）
    • Connected: ∀ p,q ∈ C: p and q are density-connected.
    • Maximal: ∀ p,q: if p ∈ C and if q is density-reachable from p (p is a core point), then q ∈ C.

提示

一个团队就像是一个集群，因为其成员之间都是相互连接的，并且它包括了所有通过团队成员可以相互到达的人，没有遗漏。

1700479099668.png

DBSCAN: The Algorithm

初始化

  • 设定参数ε（邻域大小）和MinPts（成为核心点所需的最小邻居数）。
  • 创建两个空列表：clusters用于存储集群的集合，noise用于存储噪声点。
  • 创建一个集合visited用于跟踪已经访问过的点。
  • 数据集中的每个点都会被标记为未访问。

程序主体

对于数据集中的每个点p：

  1. 检查 visited 集合来确定p是否已经处理。如果p已经访问过，则跳过此点。
  2. 将p标记为已访问（将 p 添加到 visited 集合）
  3. 获取p的 ε-Neighborhood 中的所有点， 即执行一个范围查询，找出所有与p的距离小于等于ε的点
  4. 检查邻居数量是否少于 MinPts 。
    • 如果是，将 p 标记为噪声点，添加到 noise 列表，然后继续处理下一个点。(即进行下一个循环周期)
    • 如果不是，继续下一步来形成一个新的集群。
  5. 创建一个新的集群C，并将p添加到C（这里C是一个新的列表或集合）
  6. 将p的所有邻居加入到C。这些邻居现在是p的直接密度可达点。
  7. 对于C中的每个点q
    1. 如果q未访问
      1. 将q标记为已访问，添加到visited集合中。
      2. 获取q的 ε-Neighborhood 中的所有点， 即执行一个范围查询，找出所有与q的距离小于等于ε的点
      3. 如果q的ε-邻域中至少有MinPts个点，这意味着q是一个核心点。因此，你将q的所有未处理的邻居点加入集群C。
    2. 如果q访问，需要再次获取q的ε-邻域或标记q，因为这已经在之前的步骤中完成。
    3. 这个过程是递归的，意味着我们不仅查看直接邻居，还要查看邻居的邻居，以此类推。
  8. 当C中没有更多的点可以加入时，当前集群完成。 将C加入到clusters列表中。

重复这个过程，直到所有点都被访问。

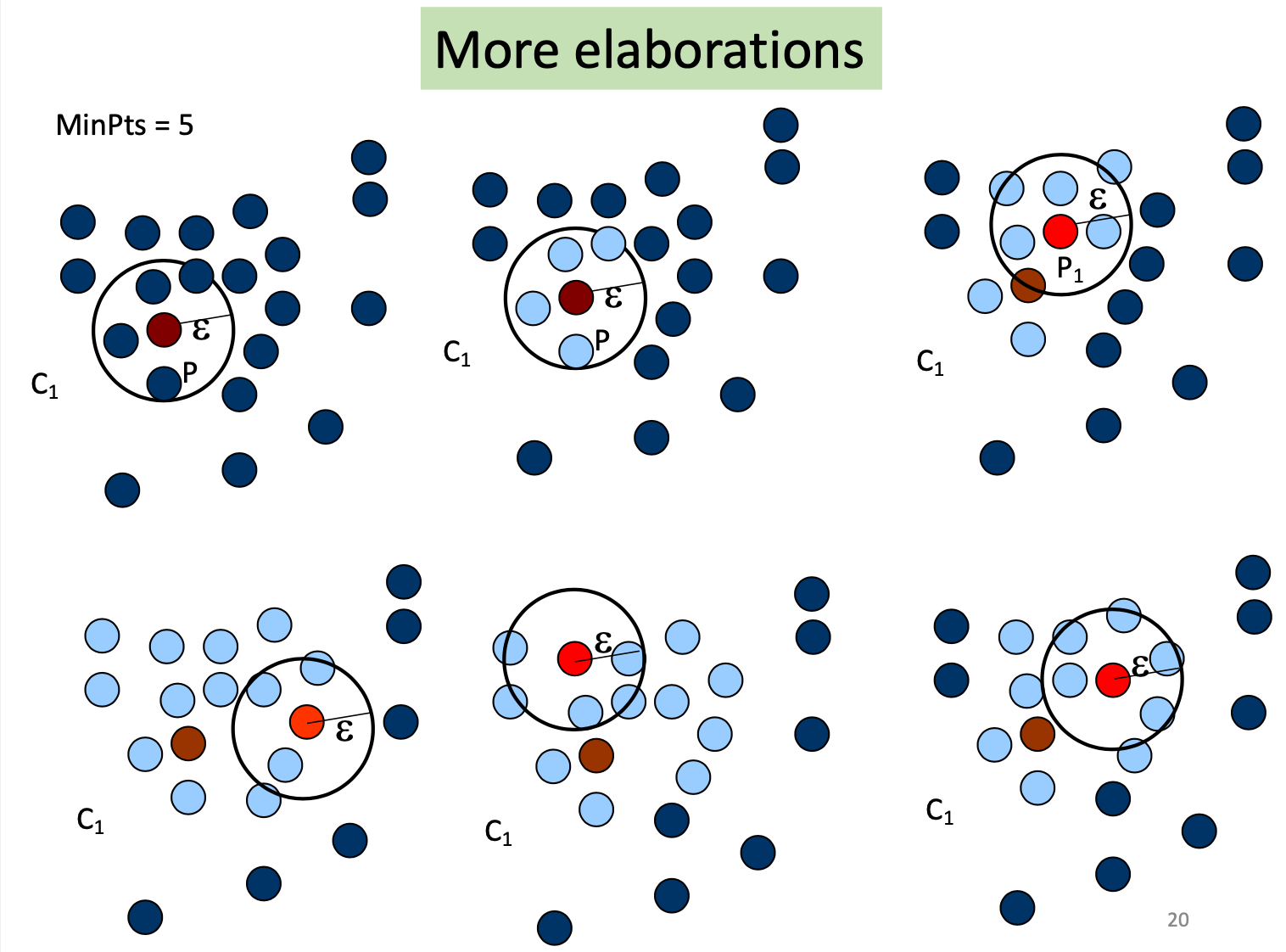
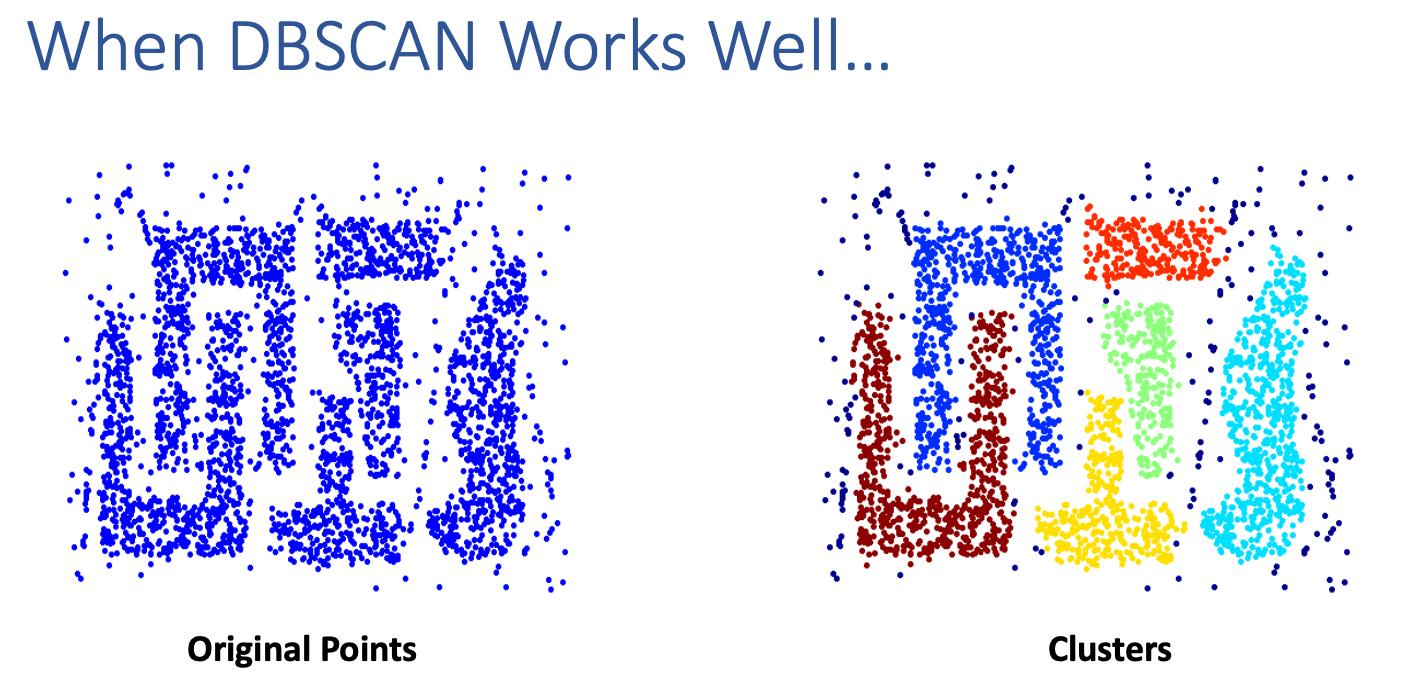
1700484681806.png1700484746906.png
  • Resistant to Noise
  • Can handle clusters of different shapes and sizes
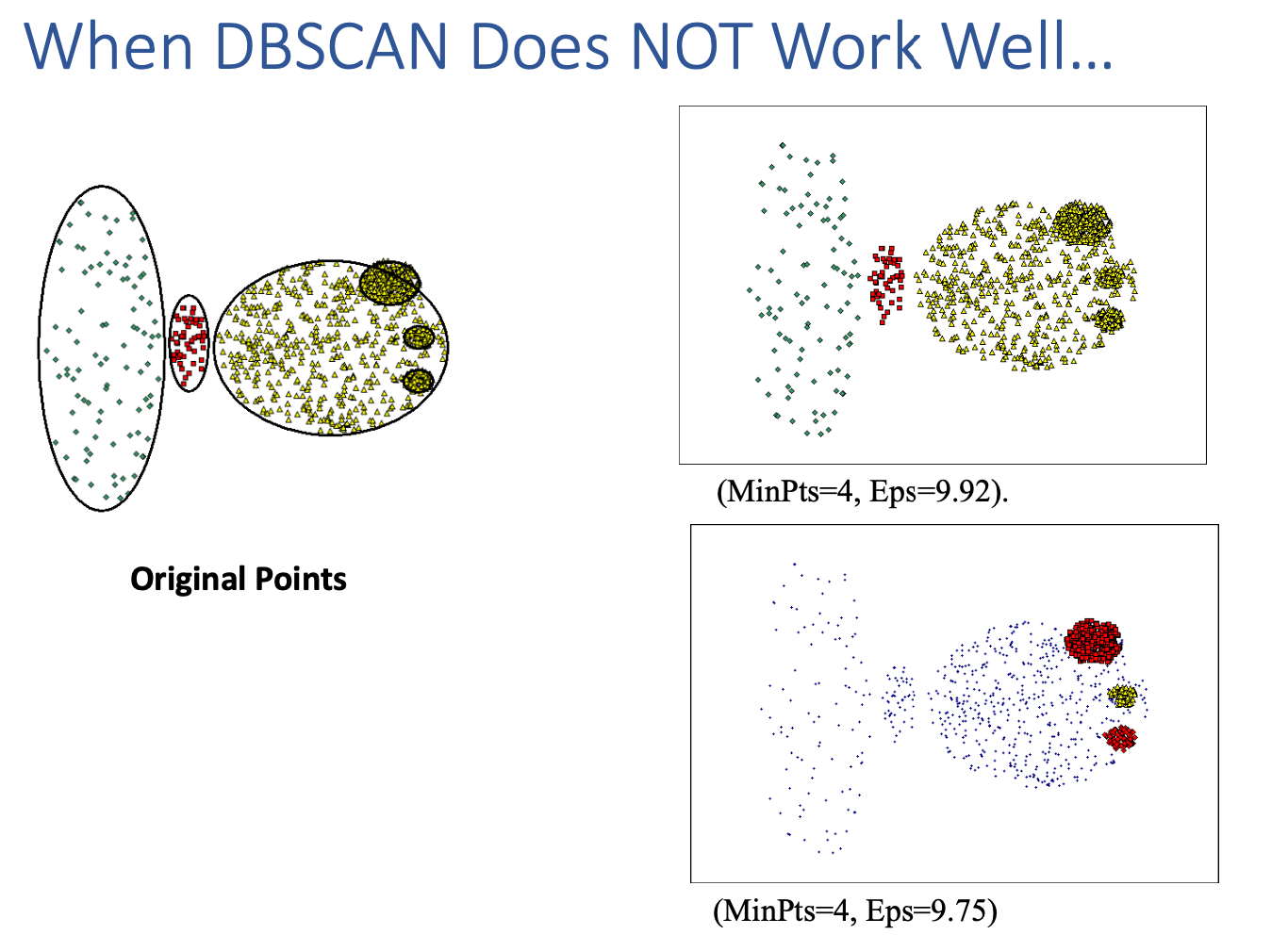
1700484833495.png
  • 对参数敏感！
  • 无法处理不同的密度！

Determining Parameters

确定DBSCAN算法中的参数ε（邻域大小）和MinPts（最小点数）是一个挑战，因为这些参数会直接影响到算法能够识别出的集群的数量和大小。

  • Cluster: 在一个区域内，如果点的数量（密度）超过了我们设定的门槛，那么这个区域就可以被称作一个集群。
  • 想法：为了找出合适的参数，我们可以考虑数据集中最不密集的那些集群。我们希望即使是这些不那么明显的集群，也能够被算法识别出来。
  • 一种找出ε的方法是观察数据点到其第k近邻的距离。这个距离可以帮助我们估计出ε的大小。
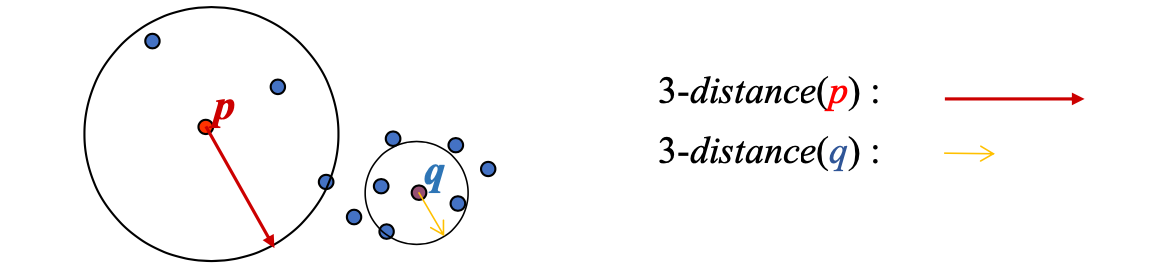
1700485392845.png
1700485392845.png
  • k-distance函数：这是一个函数，它告诉我们每个点和它的第k个最近邻居的距离是多少。
  • k-distance图：这是一个图表，它按照距离从大到小排列了所有点的k-distance值。

步骤

  1. 确定MinPts：MinPts是一个阈值，决定了一个点需要多少个邻居才能被认为是一个核心点。这个值通常取决于数据的维度（d）。一个常用的方法是将MinPts设为2 * (d - 1)。所谓维度，就是描述数据点的属性数量。比如，在一个二维空间中，每个点由两个坐标（比如x和y）来描述。
  2. 选择边界对象o：在MinPts-距离图上，用户选择一个所谓的“边界对象”。这个对象代表了边界点和核心点之间的临界点。
  3. 设定ε：一旦选择了边界对象o，ε就被设定
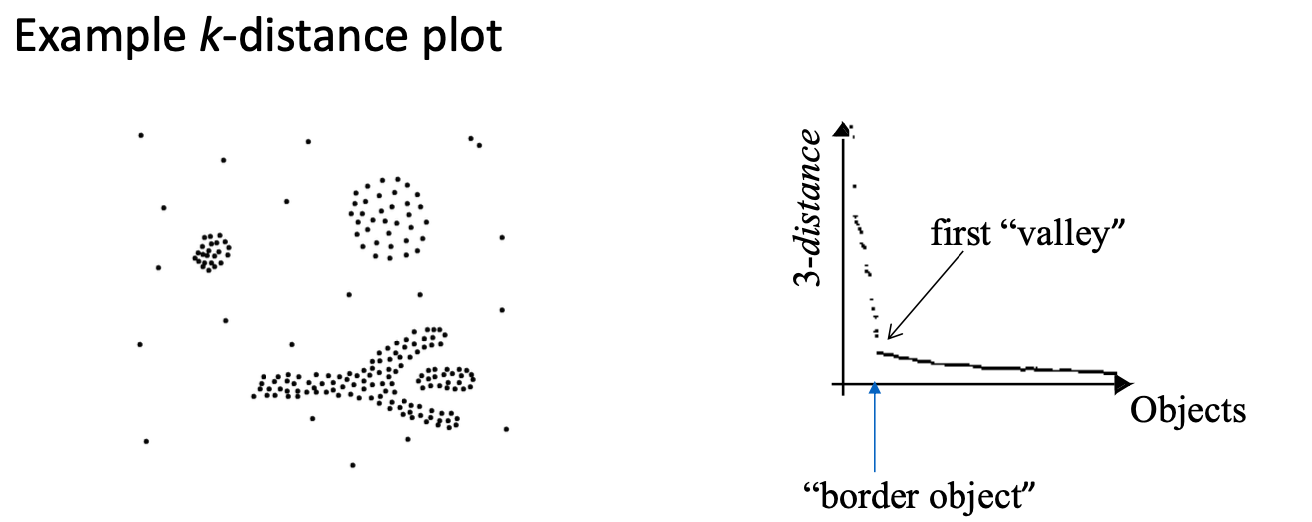
1700485875539.png
1700485875539.png

假设你正在分析一个三维空间中的星系数据（因此d=3）。根据上述公式，你将MinPts设为2 * (3 - 1) = 4。这意味着一个星系需要至少有4个邻近星系才能被认为是一个集群的核心部分。

然后，你绘制了一个MinPts-距离图，这个图显示了每个星系与其第4个最近邻星系的距离。在这个图上，你注意到有一个特定的星系o，它的第4个最近邻的距离突然比周围星系的距离大了很多。这个距离可能是100光年。

因此，你将ε设定为100光年。这意味着在你的星系数据中，如果一个星系在100光年的范围内至少有4个邻居，那么它就可以被视为一个集群的一部分。

Discussion

优势

  • 聚类可以有任意的形状和大小
  • 可自动确定聚类的数量
  • 可将聚类从周围的噪音中分离出来

缺点

  • 输入参数可能难以确定
  • 在某些情况下对输入参数设置非常敏感
Legends never die.
Copyright © 2024 Hirsun